RRB JE Elementary Statistics Questions PDF
Download Top 20 RRB JE Elementary Statistics Questions and Answers PDF. RRB JE Maths questions based on asked questions in previous exam papers very important for the Railway JE exam
Download RRB JE Elementary Statistics Questions PDF
Download RRB JE Previous Papers PDF
Question 1: Find the domain of the real function $f(x)=\frac{\log (16-x^2)}{\left \lfloor x \right \rfloor}$ where $\left \lfloor x \right \rfloor$ is the greatest integer less than or equal to x
a) (-4,4)
b) [-4,4]
c) (-4,0)U(1,4)
d) (-4,0)U[1,4)
Question 2: If $f(x)$ is polynomial of 4th degree in x and $f(x) + f(\frac{1}{x})=f(x)f(\frac{1}{x})$ and $f(2)=17$ then find $f(4)$
a) 257
b) 65
c) 96
d) None of these
Question 3: If f(x) + 2 f(1/x)=2x, find the value of f(0.25)
a) 0.75
b) 5.167
c) 2.5
d) Can’t be determined
RRB JE Free Mock Test (latest pattern)
Question 4: If the area enclosed between the inequalities $|x-a|\leq8$ and $|y-7|\leq10$ is 320, find a
a) 3
b) 1.5
c) 4
d) Can’t be determined
Question 5: Find the area enclosed between the curves $|x|+|y|\leq5$ and $2x^2+2y^2=25$
a) $25(1-\pi/2)$
b) $25(2-\pi)$
c) $25(2-\pi/2)$
d) $25(\pi/2-1)$
Question 6: How many points in the region enclosed by $y\geq|x-5|$ and $y\leq5$ have integral coordinates?
a) 42
b) 39
c) 30
d) 36
18000+ Questions – Free SSC Study Material
Question 7: A = {1, 2, 4, 5, 7, 8, 9}, B = {2, 3, 5, 7, 8, 9}
P#Q is defined as a set of all those elements which are in P and Q, but not in the both.
P@Q is defined as a set of all those elements which are present in both P and Q.
How many elements will (A@B)#(A#B) have?
a) 9
b) 8
c) 7
d) 4
Question 8: If $f(x)=x^5$, $g(x)=x^{(3/7)}$ and $h(x) = 1/x$, then for how many of the following ranges of “x” we can say that $f(x) > g(x) > h(x)$.
(I). x < – 1
(II). -1 < x < 0
(III). 0 < x < 1
(IV). x > 1
a) 0
b) 1
c) 2
d) 3
e) 4
Question 9: Let f(x)= $\max(5x, 52-2x^2)$, where x is any positive real number. Then the minimum possible value of f(x)
Question 10: Let f(x) = min (${2x^{2},52-5x}$) where x is any positive real number. Then the maximum possible value of f(x) is
Question 11: A is the set of all positive odd numbers less than 500. B is the set of the cubes of all numbers of set A. What is the number of common elements in set A and set B?
a) 3
b) 6
c) 5
d) 4
Question 12: How many integral points lie inside the region formed by the graphs |x+y| = 6 and |x-y| = 6?
Question 13: Find the number of points at which at least 2 of the following three functions intersect.
$ x^2 – 6x = 8y – y^2$
$ y = \sqrt{3}x – (6+3\sqrt{3})$
$ y -1 = x – 6\sqrt{2}$
a) 4
b) 5
c) 2
d) 3
Question 14: $|7x-5|<16$ and $|16y+11|<37$. If $x$ and $y$ are integers then find the maximum value of $|x+7|*|y-5|$
a) 63
b) 42
c) 81
d) None of These
Question 15: If f(x) is an even function and g(x) is an odd function, then how many of the following functions are even?
I. p(x) = f(g(x))
II. q(x) = g(f(x))
III. r(x) = f(x)+g(x)
IV. s(x) = f(x)*g(x)
V. t(x) = f(x)-g(x)
Question 16: What is the sum of all the values of x which satisfy $6[x]^2-37[x]+45<0$ and $x^2-2x[x]+[x]^2+1 = \frac{10}{9}$. ?
$[x]$ represents the greatest integer function.
a) 15
b) 10
c) 6
d) Cannot be determined
Daily Free Online Tests for RRB Exams
Question 17: Find the area of the region enclosed by the graph $\left|x-20\right|+\ \left|y\right|\ =\ \left|\dfrac{x}{4}\right|$ (in square units)
a) $\dfrac{190}{3}$
b) $\dfrac{160}{3}$
c) $\dfrac{100}{3}$
d) $\dfrac{250}{3}$
Question 18: A function $f(x)$ is defined as $f(x) + f(x – 1) = x^2$. If f(14) = 79 then find out the value of f(70)?
Question 19: Let f(x) be a third degree polynomial with real coefficients such that |f(2)| = |f(3)| = |f(4)| = |f(6)| = |f(7)| = |f(8)| = 12. Find out the value of |f(0)|.
a) 72
b) 96
c) 144
d) 180
Question 20: The number of integral points inside the region bounded by $|x| + |y| = 8$ but outside the region bounded by $x^2 + y^2 = 32$ is
(Exclude the points on the boundary of both the curves)
General Science Notes for RRB Exams (PDF)
Answers & Solutions:
1) Answer (D)
For the function to be a real fn $16-x^2>0$. Hence -4<x<4. Also, the divisor cannot be zero. Thus x cannot be in the range [0,1). Hence the resulting domain is (-4,4)-[0,1)=(-4,0)U[1,4)
2) Answer (A)
Let f(x)=$ax^4+bx^3+cx^2+dx+e$.
Hence, f(x) + f(1/x) = f(x)f(1/x)
=> $ax^4+bx^3+cx^2+dx+e+\frac{a}{x^4}+\frac{b}{x^3}+\frac{c}{x^2}+\frac{d}{x}+e$ = $(ax^4+bx^3+cx^2+dx+e)(\frac{a}{x^4}+\frac{b}{x^3}+\frac{c}{x^2}+\frac{d}{x}+e)$
=> $ax^4=aex^4$ => e=1, $bx^3=adx^3+bx^3$. As a!=0 => d=0. Similarly we get c=0 and b=0.
Given that f(2)=17, a=1. Hence $f(x)=x^4+1$. Hence, $f(4)=4^4+1=257$.
3) Answer (B)
f(0.25)+2f(4) = 0.5, f(4)+2f(0.25)=8. Solving simultaneous equations, f(0.25)= 5.167
4) Answer (D)
Change in a would transpose the line horizontally without changing the area enclosed. Hence a can be any number.
5) Answer (C)
The region enclosed by $|x|+|y|\leq5$ is a square with vertices at (-5,0), (0,5), (5,0) and (0,-5).
The area of the square is $(5\sqrt{2})^2=50$.
The circle is inscribed within the square touches the sides of the squares.
The area enclosed = area of square – area of circle= $50-25\pi/2 = 25(2-\pi/2)$
6) Answer (D)
First we have to plot the region enclosed by the lines of the given equation.
The equations are y = x -5 for x > 5, y = -(x – 5) for x < 5 and y = 5.
The plot of the above lines is shown below:

The region enclosed by the lines is a triangle in the first quadrant formed by the points (0,5), (5,0) and (10,5). The number of coordinates in the region with x coordinate are as follows
x=0, 1 point,
x=1, 2pts,
x=2, 3pts,
x=3, 4pts,
x=4, 5pts,
x=5, 6pts and so on.
Total points=36
7) Answer (B)
A = {1, 2, 4, 5, 7, 8, 9}
B = {2, 3, 5, 7, 8, 9}
A@B = {2, 5, 7, 8, 9}
A#B = {1, 3, 4}
(A@B)#(A#B) = {1, 2, 3, 4, 5, 7, 8, 9}
There, there are 8 elements in (A@B)#(A#B).
Hence, option B is the correct answer.
8) Answer (C)
Let us plot $f(x)$, $g(x)$ and $h(x)$ w.r.t. y.
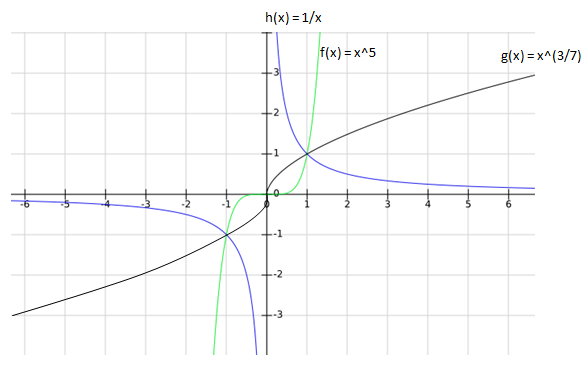
(I). x < – 1
We can see that in this range h(x) > g(x) > f(x)
(II). -1 < x < 0
We can see that in this range f(x) > g(x) > h(x)
(III). 0 < x < 1
We can see that in this range h(x) > g(x) > f(x)
(IV). x > 1
We can see that in this range f(x) > g(x) > h(x)
Therefore, we can say that for 2 ranges of x we have f(x) > g(x) > h(x). Hence, option C is the correct answer.
9) Answer: 20
The minimum value of the function will occur when the expressions inside the function are equal.
So, 5$x$ = $52 – 2x^2$
or, $2x^2 + 5x – 52$ = 0
On solving, we get $x$ = 4 or $-\dfrac{13}{2}$
But, it is given that $x$ is a positive number.
So, $x$ = 4
And the minimum value = 5*4 = 20
Hence, 20 is the correct answer.
10) Answer: 32
f(x) = min (${2x^{2},52-5x}$)
The maximum possible value of this function will be attained at the point in which $2x^2$ is equal to $52-5x$.
$2x^2 = 52-5x$
$2x^2+5x-52=0$
$(2x+13)(x-4)=0$
=> $x=\frac{-13}{2}$ or $x = 4$
It has been given that $x$ is a positive real number. Therefore, we can eliminate the case $x=\frac{-13}{2}$.
$x=4$ is the point at which the function attains the maximum value. $4$ is not the maximum value of the function.
Substituting $x=4$ in the original function, we get, $2x^2 = 2*4^2= 32$.
f(x) = $32$.
Therefore, 32 is the right answer.
11) Answer (D)
Given that A = {1, 3, 5, … 499}
B = {1, 27, 125, …, 499$^3$ }
We know that $8^3$ = 512 > 499. Hence, the number we can say that all odd positive number less than 8 are present in both set A and set B.
Therefore, we can say that there are a total of 4 elements {1, 27, 125, 343} are common in both sets. Hence, option D is the correct answer.
12) Answer: 61
The region formed by the graphs |x+y| = 6 and |x-y| = 6 is a square having vertices at (6,0),(0,6), (-6,0) and (0,-6).
Thus, excluding the points lying on x-axis and y-axis, we can say that the number of points lying in any quadrant will be the same.
Thus, let us calculate the number of points lying in the 1st quadrant and then multiply it 4.
Adding the points lying on the x-axis and y-axis will yield us the required answer.
The points lying in the first quadrant will satisfy x>0, y>0 and x+y<6
Thus, the points that satisfies these 3 equations are:-
(1,1), (1,2), (1,3), (1,4)
(2,1), (2,2), (2,3)
(3,1), (3,2)
(4,1)
Thus, there are 10 points.
Thus, the total number of points lying inside the region formed by the graphs |x+y| = 6 and |x-y| = 6 = 10*4+ 10(points on x-axis excluding the origin)+ 10(points on y-axis excluding the origin) + 1(origin)
=61
Thus, 61 points lie inside the region formed by the graphs |x+y| = 6 and |x-y| = 6.
Alternative method:-
Draw the graph as shown below and count the number of points manually.

13) Answer (C)
$ x^2 – 6x = 8y – y^2$
=> $x^2 – 6x + y^2 – 8y = 0$
=> $x^2 – 6x + 9 + y^2 – 8y + 16 = 25$
=> $(x-3)^2 + (y-4)^2 = 5^2$
Thus, the equation represents a circle with center (3, 4) and radius 5 units.
Let us find the distance between the line and the point (3,4).
If the distance is more than 5 units, then the line and the circle do not intersect.
If the distance is exactly 5 units, then the line and the circle intersect at exactly 1 point and if the distance is less than 5 unit then the line and the circle will intersect twice.
The first line is => $ y = \sqrt{3}x – (6+3\sqrt{3})$
In this line, slope $m = \sqrt{3}$, and $c = -(6+3\sqrt{3})$
Thus, the distance between the line and the center (3,4) is $\dfrac{|4 – 3\sqrt{3} + 6+3\sqrt{3}|}{\sqrt{1+(\sqrt{3})^2}}$ = $\dfrac{10}{2} = 5$
Thus, the distance is exactly 5 units and hence, there is only 1 point of intersection.
The second line is $ y -1 = x – 6\sqrt{2}$
In this line, slope $ m = 1,$ and $ c = -(6\sqrt{2} – 1)$
Thus, the distance between the line and the center of circle (3,4) is $\dfrac{|4 – 3*1 + 6\sqrt{2}-1|}{\sqrt{1+{1^2}}} = 6$
Thus, the distance between the line and the center of circle is 6 units.
6 units > 5 units and thus, there is no point of intersection.
Since, the slope of both the lines is different. they’ll intersect at 1 point( roughly at [-6.2, 1.4])
Thus, there are 2 points of intersection.
Hence, option D is the correct answer.
14) Answer (A)
$|7x-5|<16$
Therefore, $-16<7x-5<16$
=> $-11<7x<21$
=> $\frac{-11}{7}<x<3$
Thus, the maximum value of $|x+7|$ is when $x = 2$.
Thus, the maximum value of $|x+7|$ is $9$
$|16y+11|<37$
Hence, $-37<16y+11<37$
=> $-48<16y<37$
=> $-3<y<\frac{37}{16}$
Hence, the maximum value of $|y-5|$ will be when $y=-2$
Thus, the maximum value of $|y-5|$ is $7$
Therefore, the maximum value of $|x+7|*|y-5|$ is $9*7 = 63$
Hence, option A is the correct answer.
15) Answer: 2
Given, f(x) is an even function thus, f(x) = f(-x)
g(x) is an odd function thus, g(x) = -g(-x)
I. p(x) = f(g(x))
p(-x) = f(g(-x)) = f(-g(x)) = f(g(x)) = p(x)
Thus, p(x) is an even function.
II. q(x) = g(f(x))
q(-x) = g(f(-x)) = g(f(x)) = q(x)
Thus, q(x) is an even function.
III. r(x) = f(x)+g(x)
r(-x) = f(-x)+g(-x) = f(x)-g(x)
Thus, r(x) is neither odd nor even
IV. s(x) = f(x)*g(x)
s(-x) = f(-x)*g(-x) = -f(x)*g(x) = -s(x)
Thus, s(x) is an odd function
V. t(x) = f(x)-g(x)
t(-x) = f(-x)-g(-x) = f(x) + g(x)
Thus, t(x) is neither odd nor even.
Hence, only 2 of the given functions are even functions.
16) Answer (B)
$6[x]^2-37[x]+45<0$
Thus, $6[x]^2-27[x]-10[x]+45<0$
=>$([x]-\frac{5}{3})([x]-\frac{9}{2})<0$
Thus, $[x] \in (\frac{5}{3} , \frac{9}{2})$
I.e. [x] = 2, 3 and 4
$x^2-2x[x]+[x]^2+1 = \frac{10}{9}$
=> $x^2-2x[x]+[x]^2 = \frac{1}{9}$
=> $ (x-[x])^2 = \frac{1}{9}$
We know, $x-[x]>0$
=> $x-[x] = \frac{1}{3}$
Thus, $x = \frac{1}{3}+[x]$
Thus, $x = 2+\frac{1}{3} , 3+\frac{1}{3}$ and ,$ 4+\frac{1}{3}$
Thus, the required sum $= 9+1 = 10.$
Hence, option B is the correct answer.
17) Answer (B)
We are given that $\left|x-20\right|+\ \left|y\right|\ =\ \left|\dfrac{x}{4}\right|$
$\Rightarrow$ $|y| =|\dfrac{x}{4}| – |x-20|$
Case 1: When x-20 $\geq$ 0, then
$\Rightarrow$ $|y| =\dfrac{x}{4} – (x-20)$
$\Rightarrow$ $|y| =\dfrac{x}{4} – x + 20$
$\Rightarrow$ $|y| = – \dfrac{3x}{4} + 20$
Therefore, $y = + (- \dfrac{3x}{4} + 20)$ and $y = -(- \dfrac{3x}{4} + 20)$
i.e. $y = – \dfrac{3x}{4} + 20$ and $y = \dfrac{3x}{4} – 20$
Case 2: When x-20 $<$ 0, then
$\Rightarrow$ $|y| =\dfrac{x}{4} + (x-20)$
$\Rightarrow$ $|y| =\dfrac{x}{4} + x – 20$
$\Rightarrow$ $|y| = \dfrac{5x}{4} – 20$
Therefore, $y = + (\dfrac{5x}{4} – 20)$ and $y = -(\dfrac{5x}{4} – 20)$
i.e. $y = \dfrac{5x}{4} – 20$ and $y = -\dfrac{5x}{4} + 20$
Now that we have equations of all 4 sides we can easily draw the graph,

We can see the enclosed area is a kite. Hence the area of kite ABCD = $\dfrac{1}{2}*AC*BD$
$\Rightarrow$ $\dfrac{1}{2}*(5 + 5)*(\dfrac{80}{3} – 16)$
$\Rightarrow$ $\dfrac{160}{3}$
Hence, option B is the correct answer.
18) Answer: 2459
We are given that $f(x) + f(x – 1) = x^2$
By substituting x = 70, we get
$\Rightarrow$ $f(70) + f(69) = 70^2$ …(1)
By substituting x = 69, we get
$\Rightarrow$ $f(69) + f(68) = 69^2$ …(2)
By substituting x = 68, we get
$\Rightarrow$ $f(68) + f(67) = 68^2$ …(3)
By substituting x = 67, we get
$\Rightarrow$ $f(67) + f(66) = 67^2$ …(4)
By (1) – (2) + (3) – (4), we get
$\Rightarrow$ $f(70) – f(66) = 70^2 – 69^2 + 68^2 – 67^2$
$\Rightarrow$ $f(70) – f(66) = 70 + 69 + 68 + 67$
By looking at the pattern we can say that
$\Rightarrow$ $f(70) – f(14) = 70 + 69 + 68 + … + 15$
$\Rightarrow$ $f(70)$ = $(1 + 2 + 3 + … + 70)$ – $(1 + 2 + 3 + … + 14) + 79$
$\Rightarrow$ $f(70)$ = $\dfrac{70*71}{2}$ – $\dfrac{14*15}{2} + 79$
$\Rightarrow$ $f(70)$ = $2485 – 105$ + $79 = 2459$
19) Answer (D)
Let us assume that $f(x) = ax^3 + bx^2 + cx +d$ Since $f(x)$ is a third degree polynomial, it can have at most two bends in it where it goes from up to down, or from down to up.
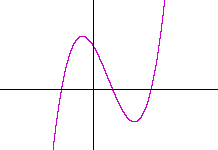
By drawing a coordinate axis, and two lines representing 12 and -12, it is easy to see that f(2)=f(6)=f(7), and f(3)=f(4)=f(8); otherwise more bends would be required in the graph. Since only the absolute value of f(0) is required, we can assume that that f(2)=12, and f(3)=-12. This provides the following system of equations.
8a + 4b + 2c + d = 12
27a + 9b + 3c + d = -12
64a + 16b + 4c + d = -12
216a + 36b + 6c + d = 12
343a + 49b + 7c + d = 12
512a + 64b + 8c + d = -12
Solving for a, b, c, and d we get a = -2, b = 30, c = -136, d = 180.
Hence we can say that |f(0)| = d = 180. Therefore option D is the correct answer.
20) Answer: 16
$x^2 + y^2 = 32$ is a circle with radius $\sqrt{32}$ = $5.xx$.
When $x$ = 0, $y$ = 5.xx
Therefore, points with co-ordinates (6,0) and (7,0) will lie outside the circle, but inside the region bounded by $|x| + |y| = 8$.
$x$ = 0 represents $Y$ axis. Since both the curves are symmetric, we can infer that 2 such points must be present along $X$, $X’$, $Y$ and $Y’$. Therefore, there will be 8 such points.
When $x$ = 1, $y$ = $\sqrt{32-1}$ = $\sqrt{31}$ = $5.xx$
$|x| + |y| = 8$
When $|x| = 1$, $|y|$ will be $7$.
The point (1,6) will lie inside the boundary.
When $x$ = 2, $y$ = $\sqrt{32-4}$ = $\sqrt{28}$ = $5.xx$
$|x| + |y| = 8$
When $|x| = 2$, $|y|$ will be $6$.
The point (2,6) will lie on the boundary and hence, we have to exclude this point.
When $x$ = 3, $y$ = $\sqrt{32-9}$ = $\sqrt{23}$ = $4.xx$
$|x| + |y| = 8$
When $|x| = 3$, $|y|$ will be $5$.
The point (3,5) will lie on the boundary and hence, we have to exclude this point.
When $x$ = 4, $y$ = $\sqrt{32-16}$ = $\sqrt{16}$ = $4$
$|x| + |y| = 8$
When $|x| = 4$, $|y|$ will be $4$.
The point (4,4) will lie on the boundary of both the curves and hence, we have to exclude this point.
When $x$ = 5, $y$ = $\sqrt{32-25}$ = $\sqrt{7}$ = $2.xx$
$|x| + |y| = 8$
When $|x| = 5$, $|y|$ will be $3$.
The point (5,3) will lie on the boundary and hence, we have to exclude this point.
When $x$ = 6, $|y|$ will be 2.
The circle cannot extend beyond $x = 5.xx$. Therefore, the point (6,2) will lie on the boundary.
When $x$ = 7, $|y|$ will be 1. Therefore, the points (6,1) will be present between the 2 regions.
Therefore, there will be 2 points (1,6) and (6,1) in the first quadrant. By symmetry, there will be 8 such points across all the 4 quadrants.
Therefore, the total number of integral points between the 2 curves = 8 (Points on the axes) + 8 = 16.
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Elementary Statistics Questions for RRB JE Exam will be highly useful for your preparation.





