Ratio And Proportion Problems For SSC CGL
Download SSC CGL Ratio and Proportion questions with answers PDF based on previous papers very useful for SSC CGL exams. 20 Very important Ratio and Proportion objective questions (MCQ’s) for SSC exams.
Download Ratio And Proportion Problems For SSC CGL
Get 200 SSC mocks for just Rs. 249. Enroll here
Question 1: A trader has 800 kg of sugar of which a part of it has been sold at 4% profit and the rest has been sold at 12% profit. On the whole, the profit is 8%. Find the quantity of sugar which he had sold it at 12% profit.
a) 360 kg
b) 500 kg
c) 280 kg
d) 400 kg
Question 2: A shopkeeper has 600 kg of rice of which a part of it has been sold at 6% profit and the rest has been sold at 4% loss. On the whole, he had no profit and no loss. Find the quantity which he had sold at loss.
a) 240 kg
b) 360 kg
c) 420 kg
d) 480 kg
Question 3: Three samples of soda and wine mixture have soda to wine ratio as 1:3,4:3 and 2:3. A new sample consisting of 1 litre each of each sample is prepared. What is the soda to wine ratio in the new sample ?
a) 167:251
b) 171:249
c) 169:253
d) 175:253
Question 4: Three containers whose volumes are in the ratio of 2 : 3 : 4 are full of mixture of spirit and water. In the 1st container, the ratio of spirit and water is 4: 1, in the 2nd container the ratio is 11 : 4 and in the 3rd container ratio is 7: 3. All the three mixture are mixed in a big container. The ratio of spirit and water in the resultant mixture is :
a) 4 : 9
b) 11 : 4
c) 5 : 10
d) 9 : 5
Question 5: The ratio between the ages of x and y at present is 3:4. Five years hence, the ratio of their ages will be 4:5; what is the present age of y in years ?
a) 15
b) 20
c) 25
d) 30
SSC CGL Previous Papers Download PDF
SSC CHSL PREVIOUS PAPERS DOWNLOAD
Question 6: An amount of money is to be distributed among P, Q and R in the ratio of 5:9:17 respectively. If the total of the shares of P and Q is Rs.7,000. What is R’s share in it
a) Rs.4,500
b) Rs.2,500
c) Rs.8,500
d) Rs.6,000
Question 7: Gold is 19 times as heavy as water and copper is 9 times as heavy as water. In what ratio should these be mixed to get an alloy 15 times as heavy as water ?
a) 1 : 1
b) 2 : 1
c) 1 : 2
d) 3 : 2
Question 8: The ages of x and y are in the ratio 3:1. Fifteen years hence, the ratio will be 2:1. The present ages (in years) are:
a) 30, 10
b) 45, 15
c) 21, 7
d) 60, 20
Question 9: In a school $\ \frac{1}{10}\ $of the boys are same in number as $\ \frac{1}{4}\ $of the girls and$\ \frac{5}{8}\ $of the girls are same in number as $\ \frac{1}{4}\ $of the boys. The ratio of the boys to girls in that school is
a) 2 : 1
b) 5 : 2
c) 4 : 3
d) 3 : 2
Question 10: The perimeter of a triangle and an equilateral triangle are same. Also, one of the sides of the rectangle is equal to the side of the triangle. The ratio of the areas of the rectangle and the triangle is
a) $\sqrt{3}\ $: 1
b) 1 :$\ \sqrt{3}$
c) 2: $\ \sqrt{3}$
d) 4 : $\ \sqrt{3}$
18000+ Questions – Free SSC Study Material
Question 11: The time required for a boy to travel along the external and internal boundaries of a circular path are in the ratio 20: 19. If the width of the path be 5 metres, the internal diameter is:
a) 195 metres
b) 192 metres
c) 180 metres
d) 190 metres
Question 12: If x, y are rational numbers and $\frac{5+\sqrt{11}}{3-2\sqrt{11}}$= x + y$\ \sqrt{11}$. The values of x and y are
a) x = $\ \frac{-14}{17}, y = \frac{-13}{26}$
b) x =$\ \frac{4}{13}, y = \frac{11}{17}$
c) x =$\ \frac{-27}{25}, y = \frac{-11}{37}$
d) x =$\ \frac{-37}{35}, y = \frac{-13}{35}$
Question 13: The three angles of a triangle are in the ratio 3 : 4 : 5. Then the angles respectively are:
a) $45^\circ,60^\circ, 75^\circ$
b) $60^\circ,45^\circ, 75^\circ$
c) $60^\circ,75^\circ, 45^\circ$
d) $75^\circ,60^\circ, 45^\circ$
Question 14: Radius of hemisphere is thrice than that of a sphere. What is the ratio of total surface area of hemisphere to that of sphere?
a) 27 : 8
b) 21 : 4
c) 27 : 4
d) 6 : 1
Question 15: Three bottles of equal capacity are containing a mixture of milk and water in ratio 2 : 1, 3 : 7 and 4 : 11 respectively. These three bottles are emptied into a large bottle. What is the ratio of milk and water respectively in this large bottle?
a) 37 : 53
b) 37 : 90
c) 37 : 30
d) 7 : 30
Question 16: The ratio of the speed of P, Q and R is 10 : 12 : 15 respectively. What is the ratio of the time taken by P, Q and R respectively to cover the same distance?
a) 10 : 12 : 15
b) 15 : 12 : 10
c) 6 : 5 : 4
d) 4 : 5 : 6
Question 17: If the height of a given cone became thrice and the radius of the base remains the same. What is the ratio of the volume of the given cone and the volume of the second cone?
a) 1 : 3
b) 1 : 9
c) 1 : √3
d) 1 : 27
Question 18: In what ratio wheat at Rs 32/kg should be mixed with wheat at Rs 24/kg so that on selling the mixture at Rs 39/kg there is a profit of 30%?
a) 3 : 1
b) 2 : 3
c) 1 : 4
d) 2 : 5
Question 19: If 2A = 3B = 5C, then what is A : B : C?
a) 2 : 3 : 5
b) 5 : 3 : 2
c) 6 : 10 : 15
d) 15 : 10 : 6
Instructions
The given pie chart shows the expenditure (in degrees) incurred in making a book.
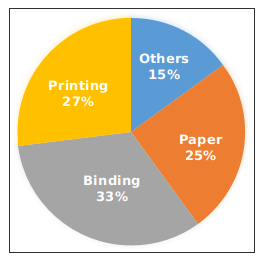
Question 20: In Others there are only two types of expenditures viz. Marketing and Distribution in ratio 3 : 2 respectively. What will be the central angle (in degrees) made by the sector of expenditure on Marketing?
a) 21.6
b) 32.4
c) 27
d) 36
1500+ Free SSC Questions & Answers
Answers & Solutions:
1) Answer (D)
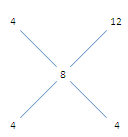
Quantity sold at 4% profit : Quantity sold at 12% profit = 4 : 4 = 1 : 1
Hence, the quantity of sugar he sold at 12% profit = $\dfrac{1}{2} \times 800 = 400 kg$
2) Answer (B)
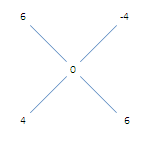
Quantity at 6% profit : Quantity at 4% loss = 4 : 6 = 2 : 3
Hence, The quantity of rice sold at loss = $\dfrac{3}{5} \times 600 = 360 kg$
3) Answer (B)
By taking the amount of soda in each sample we have 1/4,4/7,2/5
and wine as 3/4,3/7,3/5
Total soda content in new sample is ((1/4)+(4/7)+(2/5))=171/140
Total wine content in new sample is ((3/4)+(3/7)+(3/5))=249/140
Ratio =171:249
4) Answer (B)
Let volume of each container be 30, 45, 60 litres respectively.
In 1st container, spirit = $\frac{4}{(4+1)}\times30=24$ litres
=> Water = $30-24=6$ litres
Similarly, in 2nd container, spirit = 33 litres and water = 12 litres
And in 3rd container, spirit = 42 litres and water = 18 litres
After mixing, total spirit = $24+33+42=99$ litres and water = $6+12+18=36$ litres
$\therefore$ Required ratio = 11 : 4
=> Ans – (B)
5) Answer (B)
Let the present ages of x and y be 3a,4a respectively
After 5 years, their ages will be 3a+5 and 4a+5
$\frac{3a+5}{4a+5} = \frac{4}{5}$
==> 5(3a+5) = 4(4a+5)
==> 15a+25 = 16a+20
==> a=5
Present age of x = 3*5=15 years
Present age of y = 4*5=20 years
100+ Free GK Tests for SSC Exams
6) Answer (C)
Let the amount distributed among P, Q and R be 5x, 9x and 17x respectively
Total shares of P and Q is 7,000 (given) i.e
$\Rightarrow$ 5x + 9x = 7,000
$\Rightarrow$ 14x = 7,000 (or) x = 500
$\therefore$ R’s share = 17(500) = 8,500
Hence, option C is the correct answer.
7) Answer (D)
Gold is 19 times as heavy as water i.e G = $19W$
Copper is 9 times as heavy as water i.e C = $9W$
Let both the metals be mixed in the ratio of $A : B$. Then,
$\frac{A(G)}{A + B} + \frac{B(C)}{A + B} = 15W$
$A(19W)+ B(9W) = 15W(A + B)$
$19A+ 9B = 15A + 15B$
$4A = 6B$
$A : B = 3 : 2$
Hence, option D is the correct answer.
8) Answer (B)
Let the present ages of x and y be $3x$ and $x$
The ratio between the ages of x and y after 15 years will be 2:1
$\Rightarrow \frac{3x + 15}{x + 15} = \frac{2}{1}$
$\Rightarrow 3x + 15 = 2x + 30$
$\Rightarrow x = 15$
$\therefore$ Present ages of x and y are 45 and 15 respectively.
Hence, option B is the correct answer.
9) Answer (B)
Let the number of Boys be ‘B’ and the number of girls be ‘G’
$\frac{1}{10}$B=$\frac{1}{4}G$
$\Rightarrow\frac{B}{G}$= $\frac{5}{2}$
$\therefore$ B:G=5:2
10) Answer (C)
Given that the perimeters of rectangle and triangle are equal
Let the length and breadth of rectangle be ‘l’ and ‘b’ respectively
Let the side of triangle be ‘a’
$\Rightarrow$ 2(l+b)=3a
Given that one side of rectangle of rectangle = side of triangle
Let l=a
$\Rightarrow$ 2(a+b)=3a
$\Rightarrow$ 2a+2b=3a
$\Rightarrow$ a=2b
Area of rectangle : Area of triangle = ab : $\frac{\sqrt{3}}{4}a^{2}$
Substituting a=2b in above equation
$\Rightarrow$ $2b^{2} : \frac{\sqrt{3}}{4}\times4b^{2}$
$\Rightarrow 2:\sqrt{3}$
11) Answer (D)
Let internal radius of the path be $r$ m and thus external radius = $(r+5)$ m
As, distance $\propto$ time
=> $\frac{2\pi (r+5)}{2\pi r}=\frac{20}{19}$
=> $19r+95=20r$
=> $20r-19r=r=95$
$\therefore$ Internal diameter = $2\times95=190$ m
=> Ans – (D)
12) Answer (D)
$\frac{5+\sqrt{11}}{3-2\sqrt{11}} = x+y\sqrt{11}$
Rationalising above equation
$\frac{5+\sqrt{11}}{3-2\sqrt{11}}\times \frac{3+2\sqrt{11}}{3+2\sqrt{11}} = x+y\sqrt{11}$
$\Rightarrow \frac{15+10\sqrt{11}+3\sqrt{11}+22}{9-44} = x+y\sqrt{11}$
$\Rightarrow \frac{37+13\sqrt{11}}{-35} = x+y\sqrt{11}$
$\Rightarrow$ ($\frac{-37}{35})$+($\frac{-13}{35}$)$\sqrt{11} =$ $x+y\sqrt{11}$
Comparing above equations
x $= \frac{-37}{35}$ and y $= \frac{-13}{35}$
15000 Questions – Free SSC Study Material
13) Answer (A)
Ratio between angles= 3:4:5
Total parts=3+4+5=12 parts
Total angle in triangle=$180^\circ$
12 parts$\rightarrow 180^\circ$
then 1 part$\rightarrow 15^\circ$
\therefore Angles in the triangle are
$15\times3=45^\circ$
$15\times4=60^\circ$
$15\times5=75^\circ$
14) Answer (C)
Let radius of sphere = $r$ cm and radius of hemisphere = $3r$ cm
Ratio of surface area = $\frac{3\pi (3r)^2}{4\pi r^2}$
= $\frac{27}{4}$
=> Ans – (C)
15) Answer (A)
Let capacity of each bottle = L.C.M.(3,10,15) = 30 litres
=> Milk in first bottle = $\frac{2}{2+1}\times30=20$ litres
and water in first bottle = $30-20=10$ litres
Similarly, in 2nd bottle, milk = 9 litres and water = 21 litres
In 3rd bottle, milk = 8 litres and water = 22 litres
=> Total quantity of milk = $20+9+8=37$ litres
and water = $10+21+22=53$ litres
$\therefore$ Required ratio = 37 : 53
=> Ans – (A)
16) Answer (C)
Speed is inversely proportional to time.
=> Ratio of time taken = $\frac{1}{10}:\frac{1}{12}:\frac{1}{15}$
L.C.M.(10,12,15) = 60
= $\frac{60}{10}:\frac{60}{12}:\frac{60}{15}$
= $6:5:4$
=> Ans – (C)
17) Answer (A)
Let radius of given cone = $r$ and height = $h$
Height of new cone = $3h$
Volume of cone = $\frac{1}{3}\pi r^2h$
Thus, required ratio = $\frac{\frac{1}{3}\pi r^2h}{\frac{1}{3}\pi r^2(3h)}=\frac{1}{3}$
$\therefore$ Ratio of the volume of the given cone and the volume of the second cone = 1 : 3
=> Ans – (A)
18) Answer (A)
Selling price of mixture after 30% profit = Rs. 39/kg
=> Cost price of mixture = $39\times\frac{100}{130}=Rs.$ $30$ per kg
Let ratio in which wheat at Rs 32/kg should be mixed with wheat at Rs 24/kg = $x:y$
According to ques,
=> $32x+24y=30(x+y)$
=> $32x+24y=30x+30y$
=> $32x-30x=30y-24y$
=> $2x=6y$
=> $\frac{x}{y}=\frac{6}{2}=\frac{3}{1}$
$\therefore$ Ratio in which wheat at Rs 32/kg should be mixed with wheat at Rs 24/kg = 3 : 1
=> Ans – (A)
19) Answer (D)
Given : 2A = 3B = 5C
Now, L.C.M. (2,3,5) = 30
=> A : B : C = $(\frac{30}{2}):(\frac{30}{3}):(\frac{30}{5})$
= $15:10:6$
=> Ans – (D)
20) Answer (B)
Expenditure (in %) in others = 15%
Expenditure on Marketing (in %) = $\frac{3}{(3+2)}\times15=9\%$
=> Central angle (in degrees) made by the sector of expenditure on Marketing = $\frac{9}{100}\times360^\circ$
= $32.4^\circ$
=> Ans – (B)
DOWNLOAD APP FOR SSC FREE MOCKS
We hope this Ratio and Proportion questions for SSC Exam will be highly useful for your preparation.





