Quant Questions for XAT
Download important Quant Questions for XAT PDF based on previously asked questions in CAT exam. Practice Quant Questions PDF for XAT exam.
Download Quant Questions for XAT
Get 5 XAT mocks for Rs. 299. Enroll here
Question 1: Two diagonals of a parallelogram intersect each other at coordinates (17.5, 23.5). Two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16). Find the lengths of the diagonals.
a) 15 and 30
b) 15 and 40
c) 17 and 30
d) 17 and 40
e) Multiple solutions are possible
Question 2: If the last 6 digits of [(M)! – (N)!] are 999000, which of the following option is not possible for (M) × (M – N)? Both (M) and (N) are positive integers and M > N. (M)! is factorial M.
a) 150
b) 180
c) 200
d) 225
e) 234
Question 3: A circular road is constructed outside a square field. The perimeter of the square field is 200 ft. If the width of the road is 7√2 ft. and cost of construction is Rs. 100 per sq.ft. Find the lowest possible cost to construct 50% of the total road.
a) Rs. 70,400
b) Rs. 125,400
c) Rs. 140,800
d) Rs. 235,400
e) None of the above
Question 4: Akhtar plans to cover a rectangular floor of dimensions 9.5 meters and 11.5 meters using tiles. Two types of square shaped tiles are available in the market. A tile with side 1 meter costs Rs. 100 and a tile with side 0.5 meters costs Rs. 30. The tiles can be cut if required. What will be the minimum cost of covering the entire floor with tiles?
a) 10930
b) 10900
c) 11000
d) 10950
e) 10430
Question 5: Consider the set of numbers {1, 3, $3^{2}$, $3^{2}$,……,$3^{100}$}. The ratio of the last number and the sum of the remaining numbers is closest to:
a) 1
b) 2
c) 3
d) 50
e) 99
Question 6: If a, b and c are 3 consecutive integers between -10 to +10 (both inclusive), how many integer values are possible for the expression?
$\frac{a^3+b^3+c^3+3abc}{(a+b+c)^2}$=?
a) 0
b) 1
c) 2
d) 3
e) 4
Question 7: The sum of series, (-100) + (-95) + (-90) + …………+ 110 + 115 + 120, is:
a) 0
b) 220
c) 340
d) 450
e) None of the above
Question 8: If $x$ and $y$ are real numbers, the least possible value of the expression $4(x – 2)^{2} + 4(y – 3)^{2} – 2(x – 3)^{2}$ is :
a) – 8
b) – 4
c) – 2
d) 0
e) 2
Question 9: If $N = (11^{p + 7})(7^{q – 2})(5^{r + 1})(3^{s})$ is a perfect cube, where $p, q, r$ and $s$ are positive integers, then the smallest value of $p + q + r + s$ is :
a) 5
b) 6
c) 7
d) 8
e) 9
Question 10: Find the value of the expression: $10 + 10^3 + 10^6 + 10^9$
a) 1010101010
b) 1001000010
c) 1001000110
d) 1001001010
e) 100010001010
XAT Decision making practice questions
Question 11: A girl travels along a straight line, from point A to B at a constant speed, $V_1$ meters/sec for T seconds. Next, she travels from point B to C along a straight line, at a constant speed of $V_2$ meters/sec for another T seconds. BC makes an angle 105° with AB. If CA makes an angle 30° with BC, how much time will she take to travel back from point C to A at a constant speed of $V_2$ meters/sec, if she travels along a straight line from C to A?
a) $0.53(\sqrt{3}-1)T$
b) $T$
c) $0.5(\sqrt{3}+1)T$
d) $\sqrt{3}$
e) None of the above
Question 12: Abdul, Bimal, Charlie and Dilbar can finish a task in 10, 12, 15 and 18 days respectively. They can either choose to work or remain absent on a particular day. If 50 percent of the total work gets completed after 3 days, then, which of the following options is possible?
a) Each of them worked for exactly 2 days.
b) Bimal and Dilbar worked for 1 day each, Charlie worked for 2 days and Abdul worked for all 3 days.
c) Abdul and Charlie worked for 2 days each, Dilbar worked for 1 day and Bimal worked for all 3 days.
d) Abdul and Dilbar worked for 2 days each, Charlie worked for 1 day and Bimal worked for all 3 days.
e) Abdul and Charlie worked for 1 day each, Bimal worked for 2 days and Dilbar worked for all 3 days.
Question 13: A, B, C, D and E are five employees working in a company. In two successive years, each of them got hikes in his salary as follows:
A : p% and (p+1)%,
B : (p+2)% and (p-1)%,
C : (p+3)% and (p-2)%,
D : (p+4)% and (p-3)%,
E : (p+5)% and (p-4)%.
If all of them have the same salary at the end of two years, who got the least hike in his salary?
a) E
b) D
c) C
d) A
e) B
Question 14: Let P be the point of intersection of the lines
3x + 4y = 2a and 7x + 2y = 2018
and Q the point of intersection of the lines
3x + 4y = 2018 and 5x + 3y = 1
If the line through P and Q has slope 2, the value of a is:
a) 4035
b) 1/2
c) 3026
d) 1
e) 1009
Question 15: Consider the function f(x) = (x + 4)(x + 6)(x + 8) ⋯ (x + 98). The number of integers x for which f(x) < 0 is:
a) 23
b) 26
c) 24
d) 48
e) 49
Answers & Solutions:
1) Answer (D)

Using distance formula,
$CX = \sqrt{(17.5 – 5.5)^2 + (23.5 – 7.5)^2} = \sqrt{12^2 + 16^2}$
= $\sqrt{144 + 256} = \sqrt{400} = 20$
=> $AC = 2 \times CX = 40$
$BX = \sqrt{(17.5 – 13.5)^2 + (23.5 – 16)^2} = \sqrt{4^2 + 7.5^2}$
= $\sqrt{16 + 56.25} = \sqrt{72.25} = 8.5$
=> $BD = 2 \times BX = 17$
2) Answer (B)
3) Answer (B)

Perimeter of square ABCD = 200 ft
=> AB = $\frac{200}{4} = 50$ ft
=> $DB = \sqrt{50^2 + 50^2} = 50 \sqrt{2}$ ft
=> $BO = r = \frac{50 \sqrt{2}}{2} = 25 \sqrt{2}$ ft
Width of the road = BX = $7 \sqrt{2}$ ft
=> $BX = R = 25 \sqrt{2} + 7 \sqrt{2} = 32 \sqrt{2}$
Area of bigger circle = $\pi R^2 = \pi (32 \sqrt{2})^2 = 2048 \pi$ sq. ft
Area of smaller circle = $\pi r^2 = \pi (25 \sqrt{2})^2 = 1250 \pi$ sq. ft
=> Area of road = $2048 \pi – 1250 \pi = 798 \times \frac{22}{7} = 2508$ sq. ft
But we have to calculate cost of construction of 50% road.
Required Construction = $\frac{2508}{2} = 1254$ sq. ft
$\therefore$ Cost of 1254 ft = $1254 \times 100 = Rs. 1,25,400$
4) Answer (A)
Area of rectangular floor = $9.5 \times 11.5$
= $109.25 m^2$
Now, cost of covering $109 m^2$ (with 1×1 tiles) = $109 \times 100$ = Rs. 10,900
Cost of covering $0.25 m^2$ (with 0.5 m square tile) = Rs. 30
$\therefore$ Total cost = $10,900 + 30 = Rs. 10,930$
5) Answer (B)
Set : {$1, 3, 3^{2}, 3^{2},……,3^{100}$}
Clearly, this set is a G.P. with common ratio, $r = 3$
Sum of G.P. = $\frac{a (r^n – 1)}{r – 1}$
Number of terms = 101
Last term = $3^{100}$
Sum of remaining terms = $\frac{1 (3^{100} – 1)}{3 – 1}$
= $\frac{3^{100} – 1}{2}$
$\therefore$ Required ratio = $\frac{3^{100}}{\frac{3^{100} – 1}{2}}$
= $\frac{3^{100} \times 2}{3^{100} – 1}$
$\approx \frac{3^{100} \times 2}{3^{100}} = 2$
Download XAT General Knowledge PDFs
Practice Online Gk tests for XAT
6) Answer (C)
Since a,b,c are consecutive integers
=> $a = b-1$ and $c = b+1$
Expression : $\frac{a^3+b^3+c^3+3abc}{(a+b+c)^2}$
= $\frac{(b – 1)^3 + b^3 + (b + 1)^3 + 3 (b – 1) b (b + 1)}{(b – 1 + b + b + 1)^2}$
= $\frac{b^3 + 3b + b^3 + b^3 + 3b + 3b^3 – 3b}{9 b^2}$
= $\frac{6 b^3 + 3 b}{9 b^2} = \frac{2 b^2 + 1}{3 b}$
Putting different values of b from – 10 to 10, we can verify that only – 1 and 1 satisfies to get integer values for the expression.
Ans – (C)
7) Answer (D)
The given series is (-100)+ (-95)+ (-90)+….+110 + 115 + 120.
We can observe that -100 will cancel out 100, -95 will cancel out 95 and so on. Therefore, the only terms that will be remaining are 105, 110, 115 and 120.
Sum of the series = 105 + 110 + 115 + 120 = 450.
Therefore, option D is the right answer.
8) Answer (B)
$4(x – 2)^{2} + 4(y – 3)^{2} – 2(x – 3)^{2}$
$y$ is an independent variable. The value of $y$ is unaffected by the value of $x$. Therefore, the least value that the expression $4(y-3)^2$ can take is $0$ (at $y=3$).
Let us expand the remaining terms.
$4(x-2)^2-2(x-3)^2$=4*$(x^2-4x+4)-2*(x^2-6x+9)$
$=2x^2-4x-2$
=$2(x^2-2x-1)$
=$2(x^2-2x+1-2)$
=$2((x-1)^2-2)$
The least value that the expression $(x-1)^2$ can take is $0$ (at $x$ = $1$)
Therefore, the least value that the expression $2((x-1)^2-2$ can take is $2*(0-2)=2*(-2) = -4$
Therefore, option B is the right answer.
9) Answer (E)
It has been given that $N = (11^{p + 7})(7^{q – 2})(5^{r + 1})(3^{s})$ is a perfect cube. All the factors given are prime. Therefore, the power of each number should be a multiple of 3 or 0.
$p,q,r$ and $s$ are positive integers. Therefore, only the power of the expressions in which some number is subtracted from these variables or these variables are subtracted from some number can be made $0$.
$11^{p + 7}$:
This expression must be made a perfect cube. The nearest perfect cube is $11^9$. Therefore, the least value that $p$ can take is $9-7=2$.
$7^{q – 2}$
The least value that $q$ can take is 2. If $q=2$, then the value of the expression $7^{q-2}$ will become $7^0=1$, without preventing the product from becoming a perfect cube.
$5^{r+1}$:
The least value that $r$ can take is $2$.
$3^{s})$:
The least value that $s$ can take is $3$.
Therefore, the least value of the expression $p + q + r + s$ is $2+2+2+3=9$.
Therefore, option E is the right answer.
10) Answer (D)
$10 + 10^3 + 10^6 + 10^9 = 10 + 1000 + 1000000 + 1000000000$
=$1001001010$
Therefore, option D is the right answer.
11) Answer (C)
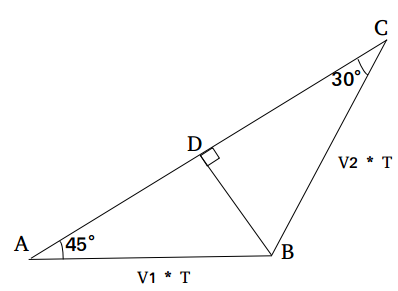
We draw BD perpendiculat to AC.
In right angled triangle BDC, BD / BC = sin 30°
or, BD = (V2 * T)/2 ……(i)
In right angled triangle BDA, BD / BA = sin 45°
Or, BD = (V1 * T)/$\sqrt{2}$ ……(ii)
From (i) and (ii), we get
V2 / V1 = $\sqrt{2}$
Total distance to be travelled from C to A = CD + DA = $\sqrt{3}$BD + BD
= BD($1 + \sqrt{3}$)
Replacing BD = (V2 * T)/2 in the avove equation,
CA = $\dfrac{\text{(V2 * T)}}{2} (1 + \sqrt{3}$)
Time taken at speed V2 = $0.5(\sqrt{3}+1)$T
Hence, option C is the correct answer.
12) Answer (E)
Let us assume the amount of work to be finished = LCM of {10, 12, 15, 18} = 180 units.
The amount of work which Abdul can complete in a day = $\dfrac{180}{10}$ = 18 units.
The amount of work which Bimal can complete in a day = $\dfrac{180}{12}$ = 15 units.
The amount of work which Charlie can complete in a day = $\dfrac{180}{15}$ = 12 units.
The amount of work which Dilbar can complete in a day = $\dfrac{180}{18}$ = 10 units.
It is given that 50 percent of the total work gets completed after 3 days. Therefore, we can say that 90 units of work was completed in 3 days.
Let us check options.
Option A: Each of them worked for exactly 2 days.
In this case amount of work completed = 2*(10+15+12+18) = 110 units.
Option B: Bimal and Dilbar worked for 1 day each, Charlie worked for 2 days and Abdul worked for all 3 days.
In this case amount of work completed = 1*(10+15)+2*(12)+3*(18) = 103 units.
Option C: Abdul and Charlie worked for 2 days each, Dilbar worked for 1 day and Bimal worked for all 3 days.
In this case amount of work completed = 1*(10)+3*(15)+2*(18+12) = 115 units.
Option D: Abdul and Dilbar worked for 2 days each, Charlie worked for 1 day and Bimal worked for all 3 days.
In this case amount of work completed = 1*(12)+3*(15)+2*(18+10) = 113 units.
Option E: Abdul and Charlie worked for 1 day each, Bimal worked for 2 days and Dilbar worked for all 3 days.
In this case amount of work completed = 1*(18+12)+2*(15)+3*(10) = 90 units.
Therefore, we can say that option E is the correct answer.
13) Answer (A)
Let the initial salary of A,B,C,D,E be $a,b,c,d,e$ respectively and let the final salary of everyone be $x$
Now, $a*(1+ \frac{p}{100})*(1+ \frac{p+1}{100}) = x$
$\Rightarrow a = \frac{x}{(1+ \frac{p}{100})*(1+ \frac{p+1}{100})}$
$\Rightarrow a = \frac{x*100*100}{(100+p)*(100+p+1)}$
$\Rightarrow a = \frac{x*100*100}{(p+100)*(p+101)}$
Similarly, $b= \frac{x}{(1+ \frac{p+2}{100})*(1+ \frac{p-1}{100})}$
$\Rightarrow b = \frac{x*100*100}{(p+102)*(p+99)}$
Similarly, $c= \frac{x}{(1+ \frac{p+3}{100})*(1+ \frac{p-2}{100})}$
$\Rightarrow c = \frac{x*100*100}{(p+103)*(p+98)}$
Similarly, $d= \frac{x}{(1+ \frac{p+4}{100})*(1+ \frac{p-3}{100})}$
$\Rightarrow d = \frac{x*100*100}{(p+104)*(p+97)}$
Similarly, $e= \frac{x}{(1+ \frac{p+5}{100})*(1+ \frac{p-4}{100})}$
$\Rightarrow e = \frac{x*100*100}{(p+105)*(p+96)}$
The numerators of the fractions are same, therefore the one with the smallest value of denominator will have the greatest value. If we compare the denominators, we can find out the fraction with the highest value. The person with the highest initial salary got the least raise, as we know that the final salary of all the candidates is same.
Thus, denominator of a, $a_{den}= (p+100)*(p+101)= p^{2}+201p+100*101$
Similarly, $b_{den}= (p+102)*(p+99)= p^{2}+201p+102*99$
$c_{den}= (p+103)*(p+98)= p^{2}+201p+103*98$
$d_{den}= (p+104)*(p+97)= p^{2}+201p+104*97$
$e_{den}= (p+105)*(p+96)= p^{2}+201p+105*96$
We see that we need to compare only the last terms of the denominators as the other terms are same.
Thus, last term of a, $a_{lt}= 100*101= 100.5^{2}-0.5^{2}$
last term of b, $b_{lt}= 102*99= 100.5^{2}-1.5^{2}$
last term of c, $c_{lt}= 103*98= 100.5^{2}-2.5^{2}$
last term of d, $d_{lt}= 104*97= 100.5^{2}-3.5^{2}$
last term of e, $d_{lt}= 105*96= 100.5^{2}-4.5^{2}$
Thus, we can see that since denominator of $e$ is the smallest, therefore E has the highest initial salary.
14) Answer (C)
On solving for x and y from the equations
3x + 4y = 2018 and 5x + 3y = 1
we get Q(-550,917)
Let, P(x,y)
So, $\frac{y – 917}{x + 550}$ = 2
=> y – 2x = 2017 ….(1)
Considering the equations
3x + 4y = 2a ……..(2)
7x + 2y = 2018 …..(3)
On subtracting equation (2) from (3) we have,
4x – 2y = 2018 – 2a
=> 2x – y = 1009 – a
=> y – 2x = a -1009 …..(4)
From equation (1) and (4)
2017 = a – 1009
=> a = 3026
Hence, option C.
15) Answer (C)
The critical points of the function are -4, -6, -8, … , -98 ( 48 points).
For all integers less than -98 and greater than -4 f(x) > 0 always .
for x= -5, f(x) < 0
Similarly, for x= -9, -13, …., -97 (This is an AP with common difference -4)
Hence, in total there are 24 such integers satisfying f(x)< 0.
We hope this Quant Questions PDF for XAT with Solutions will be helpful to you.





![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)