Quant Questions for SSC Stenographer PDF
SSC Stenographer Quant Questions and Answers download PDF based on previous year question papers of SSC exams. 20 Very important Quant Questions for Stenographer.
Download quant questions for ssc stenographer pdf
10 Stenographer Mock Tests – Just Rs. 117
Download All Important SSC Stenographer Questions PDF (Topic-Wise)
SSC Stenographer Free Mock Test (Latest Pattern)
SSC Stenographer Previous Papers
Question 1: The ratio of present ages of Rambha and Sarvesh is 8:5. After 7 years the ratio of their ages will be 5:4. What is Rambha’s present age?
a) 5
b) 30
c) 8
d) 48
Question 2: The sum of the ages of husband and wife at present is 56. Ten years ago the product of their ages was 320. What is the age of the husband and the wife?
a) 28, 28
b) 32, 24
c) 30, 26
d) 29, 27
Question 3: The value of x for which the expressions 15 - 7x and 15x + 7 become equal is .
a) -4/11
b) -11/4
c) 11/4
d) 4/11
Question 4: If 5x - 3 ≥ 3 + x/2 and 4x - 2 ≤ 6 + x; then x can take which of the following values?
a) 1
b) 2
c) -1
d) -2
Question 5: Manoj walks 12 metres towards north. Then turns right and walk another 12 metres. Then turn right and walks for 7 metres to reach college R. He again turns to his right and walks for 12 metres. What is the straight line distance (in metres) between the starting point and college R?
a) $12\sqrt2$
b) $13$
c) $14$
d) $14\sqrt3$
Download SSC Stenographer Syllabus PDF
Question 6: Which of the following statement(s) is/are TRUE ?
I. $\sqrt{324}+\sqrt{3.24}+\sqrt{0.0324} = 19.98$
II. $\sqrt{129+\sqrt{121}+\sqrt{361}+\sqrt{100}}=13$
a) Only I
b) Only II
c) Neither I nor II
d) Both I and II
Question 7: If S is 160% of T, then T will be what percent of S?
a) 85%
b) 62.50%
c) 65.20%
d) 70%
FREE SSC MATERIAL – 18000 FREE QUESTIONS
Question 8: A, B and C invest ₹14000, ₹18000 and ₹24000 respectively to start a business. If the profit at the end of the year is ₹25480, then what is total share of A and B?
a) ₹6370
b) ₹14560
c) ₹17290
d) ₹19110
Question 9: Point P (-2, 5) is the midpoint of segment AB. Co-ordinates of A are (-5, y) and B are (x, 3). What is the value of x?
a) 1
b) -1
c) 2
d) -2
1500+Free Must Solved SSC Questions (with Solutions)
Question 10: What is the slope of the line parallel to the line passing through the points (5, -1) and (4, -4)?
a) -3
b) -1/3
c) 3
d) 1/3
Question 11: The pie charts show the market share of the companies in the detergent market in 2017 and 2018. The total size of the market has decreased from ₹ 300 crores to ₹ 200 crores. What is the decrease in the sales of Company F?

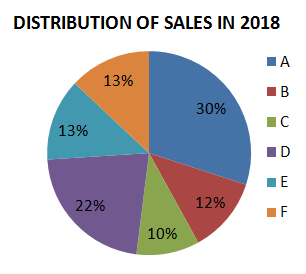
a) $14\frac{1}{3}$%
b) $12\frac{1}{3}$%
c) $33\frac{1}{3}$%
d) $13\frac{1}{3}$%
Question 12: The bar graph shows the number of cycles sold by a distributor in each month from January to June. What is the increase in the number of cycles sold in April as compared to March?

a) 75%
b) 78%
c) 68%
d) 70%
Question 13: Two positive whole numbers are such that the sum of the first and twice the second number is 8 and their difference is 2. The numbers are:
a) 7,5
b) 6,4
c) 3,5
d) 4,2
SSC STENOGRAPHER PREVIOUS PAPERS
Question 14: If Cos A + Sin A = $\sqrt{2}$ Cos A then Cos A- Sin A is equal to: (Where $0^\circ$<A<$90^\circ$)
a) $\sqrt{2SinA}$
b) $\sqrt{SinA}$
c) $\sqrt{2}Sin A$
d) 2 Sin A
Question 15: Salaries of Ravi and Sumit are in the ratio 2:3. If the salary of each is increased by ₹3000, the new ratio becomes 35:50. What is Sumit’s new salary?
a) ₹18,000
b) ₹21,000
c) ₹27,000
d) ₹30,000
Question 16: Two alloys A and B contain copper and zinc in the ratio 7 : 2 and 5 : 3 respectively. How many kg of A and B must be melted in order to get an alloy of 44 kg containing copper and Zinc in the ratio 3 : 1?
a) 24 kg, 20 kg
b) 30 kg, 14 kg
c) 28 kg, 16 kg
d) 36 kg, 8 kg
Stenographer Expected Cut off 2018-19
SSC Stenographer Salary after 7th Pay Commission
Answers & Solutions:
1) Answer (C)
Let Rambha’s present age = $8x$ years and Sarvesh’s present age = $5x$ years
According to ques, => $\frac{8x + 7}{5x + 7} = \frac{5}{4}$
=> $32x + 28 = 25x + 35$
=> $32x – 25x = 35 – 28$
=> $7x = 7$
=> $x = \frac{7}{7} = 1$
$\therefore$ Rambha’s age = $8 \times 1 = 8$ years
=> Ans – (C)
2) Answer (C)
Let husband’s age = $x$ years
=> Wife’s age = $(56 – x)$ years
According to ques, $(x-10)(56-x-10)=320$
=> $(x-10)(46-x)=320$
=> $46x-x^2-460+10x=320$
=> $x^2-56x+780=0$
=> $x^2-30x-26x+780=0$
=> $x(x-30)-26(x-30)=0$
=> $(x-30)(x-26)=0$
=> $x=30,26$
$\therefore$ Ages of the husband and the wife = 30 and 26 years
3) Answer (D)
Expressions : 15 - 7x and 15x + 7
=> $15 – 7x = 15x + 7$
=> $15x + 7x = 15 – 7$
=> $22x = 8$
=> $x = \frac{8}{22} = \frac{4}{11}$
=> Ans – (D)
4) Answer (B)
Expression 1 : 5x - 3 ≥ 3 + x/2
=> $5x-\frac{x}{2} \geq 3+3$
=> $\frac{9x}{2} \geq 6$
=> $x \geq \frac{4}{3}$ ————(i)
Expression 2 : 4x - 2 ≤ 6 + x
=> $4x-x \leq 6+2$
=> $3x \leq 8$
=> $x \leq \frac{8}{3}$ ————(ii)
Combining inequalities (i) and (ii), we get : $\frac{4}{3} \leq x \leq \frac{8}{3}$
The only value that $x$ can take among the given options = 2
=> Ans – (B)
5) Answer (B)
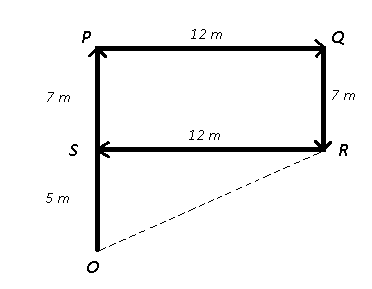
Let Manoj start from point O and walks 12 metres towards north to reach P. Then turns right and walk another 12 metres eastwards to reach Q. Then turn right and walks for 7 metres southwards to reach college R. He again turns to his right and walks for 12 metres.
Thus, $(OR)^2=(OS)^2+(SR)^2$
=> $(OR)^2=(5)^2+(12)^2$
=> $(OR)^2=25+144=169$
=> $OR=\sqrt{169}=13$ m
=> Ans – (B)
6) Answer (D)
I : $\sqrt{324}+\sqrt{3.24}+\sqrt{0.0324} = 19.98$
L.H.S. = $18+1.8+0.18=19.98=$ R.H.S.
II : $\sqrt{129+\sqrt{121}+\sqrt{361}+\sqrt{100}}=13$
L.H.S. = $\sqrt{129+11+19+10}=\sqrt{169}=13=$ R.H.S.
Thus, both I and II are correct.
=> Ans – (D)
7) Answer (B)
Given, S = 160% of T
=> $S = \dfrac{160}{100}\times T$
=> $T = \dfrac{100}{160}\times S$
=> $T = \dfrac{5}{8}S$
$\dfrac{5}{8} = 62.5$%
Hence, T = 62.5% of S
8) Answer (B)
Ratio of profits = Ratio of investments = 14000 : 18000 : 24000 = 7 : 9 : 12
Let the profit of A, B and C be Rs.7x, Rs.9x, Rs.12x respectively.
Total profit = 7x+9x+12x = Rs.28x
Given, 28x = 25480
Therefore, Profit of A and B together = Rs.7x+9x = Rs.16x = $\dfrac{16\times25840}{28} = Rs.14560$
9) Answer (A)
Mid-point = $(\frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2})$ $\Rightarrow \frac{-5+x}{2}=-2 \Rightarrow x = -4 + 5 = 1$
so the answer is option A.
10) Answer (C)
slope m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-4+1}{4-5}=-3$
slope of the parallel line = m = -3.
So the answer is option C.
11) Answer (D)
Sales of Company F in 2017 = 10% of Rs.300 crore = Rs.30 crore
Sales of Company F in 2018 = 13% of Rs.200 crore = Rs.26 crore
Decrease in sales = $\dfrac{30-26}{30}\times100 = \dfrac{40}{3}$% $= 13\dfrac{1}{3}$%
12) Answer (A)
Number of cycles sold in March = 60
Number of cycles sold in April = 105
Percentage Increase in number of cycles = $\dfrac{105-60}{60}\times100 = \dfrac{45}{60}\times100 = 75$%
13) Answer (D)
Let the numbers be $x$ and $(x-2)$
According to ques,
=> $x+2(x-2)=8$
=> $x+2x-4=8$
=> $3x=8+4=12$
=> $x=\frac{12}{3}=4$
$\therefore$ Numbers are = 4, 2
=> Ans – (D)
14) Answer (C)
Given : $cos A+sin A=\sqrt2 cos A$
Squaring both sides, we get :
=> $(cos A+sin A)^2=(\sqrt2 cos A)^2$
=> $cos^2A+sin^2A+2sin A.cos A=2cos^2A$
=> $1+2sin A.cos A=2(1-sin^2A)$
=> $1+2sin A.cos A=2cos=2-2sin^2A$
=> $2sin A.cos A=2cos=1-2sin^2A$ —————–(i)
To find : $cos A-sin A=x$
Squaring both sides, we get :
=> $x^2=cos^2A+sin^2A-2sin A.cos A$
Substituting value from equation (i),
=> $x^2=1-(1-2sin^2A)$
=> $x^2=2sin^2A$
=> $x=\sqrt{2sin^2A}$
=> $x=\sqrt2sin A$
=> Ans – (C)
15) Answer (D)
Let the salaries of ravi and sumit be 2x and 3x
salaries increased by 3000
new salaries are 2x+3000 an 3x+3000
ratio =7:10
(2x+3000)/(3x+3000)=7/10
20x+30000=21x+21000
x=9000
Sumit’s new salary=3(9000)+3000
=30000
16) Answer (D)
Copper in the A alloy=7/9
Copper in the B alloy=5/8
Copper in the resultant mixture=3/4
let the ratio in which they are mixed is x
By using the principle of allegation we have
x=((3/4)-(5/8))/((7/9)-(3/4))
x=(1/8)/(1/36)
x=9:2
Given 44 kg of mixture and so zinc copper present is (3/4)*44=33 kg
Therefore (7/9)*9y +(5/8)*2y =33
7y+(5y/4)=33
33y/4 =33
y=4
9y=36 kgs and 2y=8 kgs
We hope this Quant Questions will definitely help at the time of your preparation. Download the cracku app for daily test.





