Percentage Questions for CAT Set-3 PDF
Download important Percentage Questions for CAT Set-3 PDF based on previously asked questions in CAT exam. Practice Percentage Questions Set-3 PDF for CAT exam.
Download Percentage Questions for CAT Set-3 PDF
CAT Test series at just Rs. 299. Enroll here
Download CAT Quant Questions PDF
Take 3 Free Mock Tests for CAT
Question 1: If equal numbers of people are born on each day, find the approximate percentage of the people whose birthday will fall on 29th February. If we are to consider people born in 20th century (1901-2000) and assuming no deaths.
a) 0.374
b) 0.5732
c) 0.0664
d) None of these
Question 2: Tina, Mina, Gina, Lina and Bina are 5 sisters, aged in that order, with Tina being the eldest. Each of them had to carry a bucket of water from a well to their house. Their buckets’ capacities were proportional to their ages. While returning, equal amount of water got splashed out of their buckets. Who lost maximum amount of water as a percentage of the bucket capacity?
a) Tina
b) Mina
c) Gina
d) Lina
e) Bina
Question 3: Ram prepares solutions of alcohol in water according to customers’ needs. This morning Ram has prepared 27 litres of a 12% alcohol solution and kept it ready in a 27 litre delivery container to be shipped to the customer. Just before delivery, he finds out that the customer had asked for 27 litres of 21% alcohol solution. To prepare what the customer wants, Ram replaces a portion of 12% solution by 39% solution. How many litres of 12% solution are replaced?
a) 5
b) 9
c) 10
d) 12
e) 15
Question 4: In 2006, Raveendra was allotted 650 shares of Sun Systems Ltd in the initial public offer, at the face value of Rs. 10 per share. In 2007, Sun Systems declared the bonus at the rate of 3 : 13. In 2008, the company again declared the bonus at the rate of 2 : 4. In 2009, the company declared a dividend of 12.5%. How much dividend does Raveendra get in 2009 as a percentage of his initial investment?
a) 24.5%
b) 23.9%
c) 24.1%
d) 23%
Question 5: M/s. Devi Radiograms, a shop which sells electronic gadgets, marks its merchandise 35% above the purchase price. Until four months ago, purchase price of one Philips DVD player was Rs. 3,000. During the last four months M/s. Devi Radiograms has received four monthly consignments of Philips DVD player at the purchase price of Rs. 2,750, Rs. 2,500, Rs. 2,400, and Rs. 2250. The average rate of decrease in the purchase price of DVD player during these four months is:
a) 7.5%
b) 8.20%
c) 6.9%
d) 7%
Take 3 free mock tests for CAT
Download CAT Quant Questions PDF
Question 6: The annual production in cement industry is subject to business cycles. The production increases for two consecutive years consistently by 18% and decreases by 12% in the third year. Again in the next two years, it increases by 18% each year and decreases by 12% in the third year. Talking 2008 as the base year, what will be the approximate effect on cement production in 2012?
a) 24% increase
b) 37% decrease
c) 45% increase
d) 60% decrease
Question 7: The pre-paid recharge of Airtel gives 21% less talktime than the same price pre-paid recharge of Vodafone. The post-paid talktime of Airtel is 12% more than its pre-paid recharge, having the same price. Further, the post-paid talktime of same price of Vodafone is 15% less than its pre-paid recharge. How much percent less / more talktime (approximately) can one get from the Airtel post-paid service compared to the post-paid service of Vodafone?
a) 4.09% more
b) 4.7% less
c) 4.7%more
d) 2.8% less
Question 8: There are two alloys P and Q made up of silver, copper and aluminium. Alloy P contains 45% silver and rest aluminum. Alloy Q contains 30% silver, 35% copper and rest aluminium. Alloys P and Q are mixed in the ratio of 1 : 4 . 5. The approximate percentages of silver and copper in the newly formed alloy is:
a) 33% and 29%
b) 29% and 26%
c) 35% and 30%
d) None of the above
Question 9: The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is
a) 35
b) 50
c) 60
d) 65
Question 10: Out of the shirts produced in a factory, 15% are defective, while 20% of the rest are sold in the domestic market. If the remaining 8840 shirts are left for export, then the number of shirts produced in the factory is
a) 13600
b) 13000
c) 13400
d) 14000
Download CAT Quant Questions PDF
CAT Test series at just Rs. 299. Enroll here
Answers & Solutions:
1) Answer (D)
Assume one person is born every day. In 100 years, there will be 25 leap years. So 25*1 additional people will be born on these days.
So, total people born will be = $365 \times 100 \times 1 + 25 \times 1$
And people born on 29th february = $25 \times 1$
Hence percentage will be = $\frac{25 \times 1}{365 \times 100 \times 1 + 25 \times 1} \times 100$ = 0.0684
2) Answer (E)
Let the capacities of bucket of water carried by Tina, Mina, Gina, Lina and Bina respectively be $W_T, W_M, W_G, W_L, W_B$
It is given that : $W_T > W_M > W_G > W_L > W_B$
Let they spill $x$ litres of water from the bucket.
Thus, %age of water spilled by them respectively be
= $\frac{x}{W_T} \times 100 $, $\frac{x}{W_M} \times 100$, $\frac{x}{W_G} \times 100$, $\frac{x}{W_L} \times 100$, $\frac{x}{W_B} \times 100$
$\because W_T > W_M > W_G > W_L > W_B$
$\therefore \frac{x}{W_T} \times 100$ < $ \frac{x}{W_M} \times 100$ < $\frac{x}{W_G} \times 100$ < $\frac{x}{W_L} \times 100$ < $\frac{x}{W_B} \times 100$
Thus, Bina lost maximum amount of water as a percentage of the bucket capacity.
3) Answer (B)
Let Ram replaces $x$ litres of 12 % sol. with 39 % solution
Now, quality of 12 % solution in 27 litre = $\frac{12}{100} \times 27$
=> After replacing we have volume of 12 % solution
= $(\frac{12}{100} \times 27) – (\frac{12 x}{100}) + (\frac{39 x}{100})$
= $\frac{324 + 27 x}{100}$
This is equal to 27 litre of 21 % solution.
=> $\frac{324 + 27 x}{100} = \frac{21}{100} \times 27$
=> $27x = 567 – 324 = 243$
=> $x = \frac{243}{27} = 9$
Alternate Solution:
The mixture of two solutions 12% alcohol and 39% alcohol should yield 21% alcohol solution.
Using allegation:
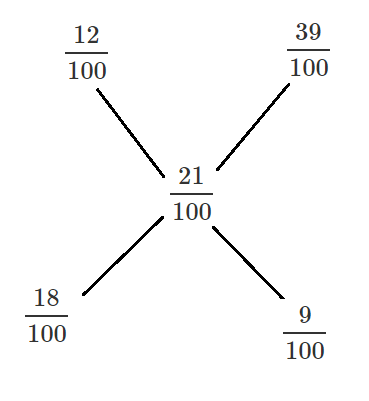
The ratio = 18/9 =2:1
So the amount of 39% solution required = 27*1/(2+1) =9
4) Answer (D)
Bonus share received in 2007 = 650 * (3/13) = 150
Bonus share received in 2008 = 800 * (1/2) = 400
So, has has (150 + 400) = 550 extra shares
Dividend of the share is always issued on face value irrespective of market value
Dividend = (Total value of shares) * (Percentage of dividend)
Dividend he will get $= \dfrac{1200 * 10 * \frac{12.5}{100}}{650 * 10} = \dfrac{1200}{650} * \dfrac{1}{8} = \dfrac{3}{13} = 23$%
Hence, option D is the correct answer.
5) Answer (C)
decrease in purchase price for first month was $\frac{3000-2750}{3000}$ = 0.083
decrease in purchase price for second month was $\frac{2750-2500}{2750}$ = 0.0909
decrease in purchase price for the third month was $\frac{2500-2400}{2500}$ = 0.04
decrease in purchase price for the fourth month was $\frac{2400-2250}{2400}$ = 0.0625
Average decrease = $\frac{0.083+0.0909+0.04+0.0625}{4}$ = 0.069 i.e 6.9%
Therefore our answer is option’C’
Free CAT Practice – Study Material
Download CAT Quant Formulas PDF
6) Answer (C)
Let 100 be the value in 2008.
In 2009 it will become 100*1.18
In 2010 it will become 100*1.18*1.18
In 2011 it will become 100*1.18*1.18*0.88
In 2012 it will become 100*1.18*1.18*0.88*1.18 $\approx$ 145
thus, the effect = 45%
Hence, option C is the correct answer.
7) Answer (A)
Let the value of pre-paid recharge of Vodafone be 100.
Then the value of pre-paid recharge of Airtel is 79.
Airtel gives 12% more to post-paid, so post-paid value is 79 x 1.12 = 88.48
Vodafone gives 15% less to post-paid than its pre-paid so its value is 85.
Clearly Airtel gives more to its post-paid customers.
Percentage = $\frac{3.48}{85}$ x 100 = 4.09%
Therefore, option A is the right answer.
8) Answer (A)
Composition of alloy P
Silver:Copper:Aluminium = 45:0:55
Composition of alloy Q
Silver:Copper:Aluminium = 30:35:35
They are mixed in ratio of 1: 4.5
Let us consider alloy P is taken 200 grams and alloy Q is taken 900 grams.
Then for alloy P :-
Silver:Copper:Aluminium = 90:0:110
For alloy Q:
Silver:Copper:Aluminium = 270:315:315
Total weight of P and Q combined is 1100 grams.
When P and Q are mixed, the new combined ratio of
Silver:Copper:Aluminium = 360:315:425
Percentage of Silver in mixture = $\frac{360}{1100}$ x 100 $\cong$ 33%
Percentage of Copper in mixture = $\frac{315}{1100}$ x 100 $\cong$ 29%
9) Answer (D)
Let the number of girls be 2x and number of boys be x.
Girls getting admission = 0.6x
Boys getting admission = 0.45x
Number of students not getting admission = 3x – 0.6x -0.45x = 1.95x
Percentage = (1.95x/3x) * 100 = 65%
10) Answer (B)
Let the total number of shirts be x.
Hence number of non defective shirts = x – 15% of x = 0.85x
Number
of shirts left for export = No of non defective shirts – number of
shirts sold in domestic market
= No of non defective shirts – 20% of No of non defective shirts
= 80% of No of non defective shirts
Hence 8840 = 0.8 * (0.85x) .
Solving for x we get, x = 13000
Download CAT Previous Papers PDF
Download Free CAT Preparation App
We hope this Percentage Questions PDF for CAT Set-3 with Solutions will be helpful to you.





![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)