Percentage and Venn Diagrams Questions for XAT 2022 – Download PDF
Download Percentage and Venn Diagrams Questions for XAT PDF – XAT Percentage and Venn Diagrams questions pdf by Cracku. Top 10 very Important Percentage and Venn Diagrams Questions for XAT based on asked questions in previous exam papers.
Download Percentage and Venn Diagrams Questions for XAT
Get 5 XAT mocks at just Rs.299
Question 1: A group of 20 girls has average age of 12 years. Average of first 12 from the same group is 13 years and what is the average age of other 8 girls in the group?
a) 10
b) 11
c) 11.5
d) Cannot be determined
e) None of these
Question 2: The total marks obtained by Jaya in the maths and Physics together are 50 more than the marks obtained by her in chemistry, if she got 20 marks in the physics .What are her marks in maths?
a) 20
b) 40
c) 80
d) Cannot Determined
e) None of these
Question 3: Two chairs and three tables cost Rs 1025/- and 3 chairs and 2 tables cost is Rs 1,100/- .What is the difference between the cost one table and chair?
a) 75
b) 35
c) 125
d) Cannot be determined
e) None of these
Question 4: The cost of 4 cell phones and 7 digital cameras is Rs 1,25,627.what is the cost of 8 cellphones and 14 digital cameras.
a) 251254
b) 252627
c) 225524
d) Cannot determined
e) None of these
Question 5: If a amount of Rs 41910 is distributed amongst 22 persons equally,how much each person get
a) 1905
b) 2000
c) 1885
d) 2015
e) None of these
Question 6: Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
a) 22
b) 21
c) 20
d) 19
Question 7: For a set S, we denote by S’, the complement of the set S. Let X, Y, Z be Sets such that $Y \subseteq X$. Which of the following is always true?
a) $X \cap Z \subseteq Y \cap Z$
b) $Y’ \cap Z’ ⊇ X’ \cap Z’$
c) $X \cap (Y \cup Z) = Y \cup (X \cap Z)$
d) $X’ \cap Z ⊇ Y’ \cap Z$
Question 8: Each student in a class of 40 plays at least one indoor game-chess, carom and scrabble. 18 play chess, 20 play scrabble and 27 play carom. 7 play both chess and scrabble, 12 play both scrabble and carom and 4 play all 3 games. The number of players who play chess and carom but not scrabble is
a) 10
b) 4
c) 6
d) 12
Question 9: A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
a) 38
b) 32
c) 45
d) 43
Question 10: 400 students were admitted to the 2018-19 MBA batch. 200 of them did not choose “Business Statistics”. 100 of them did not choose “International Management’. There were 80 students who did not choose any of the two subjects. Find the number of students who chose both Business Statistics and International Management.
a) 180
b) 220
c) 280
d) 300
Answers & Solutions:
1) Answer (E)
Let the age of each of the girl in the group be $x_1,x_2,x_3,…..,x_{20}$ years
Average age of 20 girls = 12
=> $\frac{(x_1+x_2+x_3+…..+x_{20})}{20}=12$
=> $(x_1+x_2+x_3+…..+x_{20})=12 \times 20=240$ ————(i)
Average of first 12 girls = 13
=> $\frac{(x_1+x_2+x_2+….+x_{12})}{12}=13$
=> $(x_1+x_2+x_3+…..+x_{12})=13 \times 12=156$ ———–(ii)
Subtracting equation (ii) from (i)
=> $(x_1+x_2+x_3+…..+x_{20})$ $-$ $(x_1+x_2+x_3+…..+x_{12}) = (240-156)$
=> $(x_{13}+x_{14}+…..+x_{20})=84$
Dividing above equation by 8
=> $\frac{(x_{13}+x_{14}+……+x_{20})}{8}=\frac{84}{8} = 10.5$
=> Ans – (E)
2) Answer (D)
Let marks obtained by Jaya in Physics, maths and chemistry respectively be $p,m,c$
Marks in physics, $p=20$
According to ques, => $m+p=c+50$
=> $m+20=c+50$
=> $m-c=50-20=30$
There is only 1 equation and 2 variables, thus we cannot determine the marks scored by her in maths or chemistry.
=> Ans – (D)
3) Answer (A)
Let cost price of 1 chair = $Rs.$ $x$ and cost price of 1 table = $Rs.$ $y$
=> $2x+3y=1025$ ———–(i)
and $3x+2y=1100$ ——–(ii)
Subtracting equation (i) from (ii)
=> $(3x-2x)+(2y-3y)=(1100-1025)$
=> $x-y=75$
$\therefore$ Difference between the cost one table and chair = Rs. 75
=> Ans – (A)
4) Answer (A)
Let cost of 1 cell phone = $Rs. x$ and 1 digital camera = $Rs. y$
=> $4x + 7y = 1,25,627$
Multiplying both sides by 2, we get :
=> $8x + 14y = 125627 \times 2 = 251254$
$\therefore$ Cost of 8 cellphones and 14 digital cameras = Rs. 2,51,254
5) Answer (A)
Amount distributed = Rs. 41910
Number of person = 22
Each person will get = $\frac{41910}{22}$
= Rs. 1,905
6) Answer (C)
Now 23 students choose maths as one of their subject.
This means (MPC)+ (MC) + (PC)=23 where MPC denotes students who choose all the three subjects maths, physics and chemistry and so on.
So MC + PM =5 Similarly we have PC+ MP =7
We have to find the smallest number of students choosing chemistry
For that in the first equation let PM=5 and MC=0. In the second equation this PC=2
Hence minimum number of students choosing chemistry will be (18+2)=20 Since 18 students chose all the three subjects.
7) Answer (B)

Consider the above Diagram
For option A $X\cap Z$ = c+e and $Y\cap Z$ = e. Hence option A is False
For Option B $Y’\cap Z’$ = a+u and $X’\cap Z’$ = u. Option B is True
For Option C $X\cap\left(Y\cup Z\right)$ = c+d+e and $Y\cup\left(X\cap Z\right)$ = c+d+e. Option C is True
For option D $X’\cap Z$ = b and $Y’\cap Z$ = b+c. Option D is False
8) Answer (C)
Students who play all the three games are 4, and with the rest information given in the question, we can at best draw the venn diagram as:

Now, total students=40.
So, Chess+ 5+8+15-x=40
=>18+28-x=40
=> 46-x=40
.’. x=6
9) Answer (D)
Assume the number of members who can play exactly 1 game = I
The number of members who can play exactly 1 game = II
The number of members who can play exactly 1 game = III
I+2II+3III=144+123+132=399….(1)
I+II+III=256……(2)
=> II+2III=143…..(3)
Also, II+3III=58+25+63=146 ……(4)
=> III = 3 (From 3 and 4)
=> II =137
=> I = 116
The members who play only tennis = 123-58-25+3 = 43
10) Answer (A)
The number of students in 2018-19 MBA batch = 400
Number of students who did not choose ‘Business Statistics’ = 200
Number of students who did not choose ‘International Management’ = 100
Number of students who did not choose any of the two subjects = 80
Number of students who choose at least one of the two subjects = 400-80=320
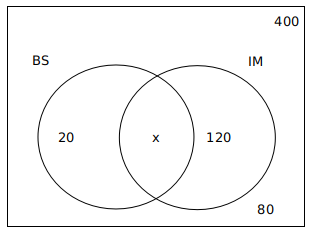
140+x=320
x=320-140=180
A is the correct answer.
Download XAT previous papers [PDF]
We hope these Percentage and Venn Diagrams questions for XAT pdf for the XAT exam will be highly useful for your preparation.





