Number System Questions For SSC GD PDF Set – 2
SSC GD Constable Number System Question paper with answers download PDF based on SSC GD exam previous papers. 40 Very important Number System questions for GD Constable.
DOWNLOAD NUMBER SYSTEM QUESTIONS FOR SSC GD PDF SET – 2
GET 20 SSC GD MOCK FOR JUST RS. 117
Download SSC GD Important Questions PDF
1500+ Must Solve Questions for SSC Exams (Question bank)
Question 1: 25% of 48 + 50% of 120 + 70% of 75 + 14% of 45 = ?% of 327
a) 42
b) 44
c) 50
d) 40
Question 2: The ratio of two numbers is 5:13. If the product of the numbers is 3185, what is the sum of the square of the two numbers?
a) 4753
b) 1986
c) 7056
d) 9506
Question 3: What is the units digit of $7^{79}+13^{62}$?
a) 1
b) 5
c) 2
d) 0
Question 4: What is the least number which when divided by 2, 3, 4. 5, and 6 leaves remainder of 1, 2, 3, 4 and 5 respectively?
a) 129
b) 77
c) 179
d) 59
Question 5: The sum of 5 numbers is 70. When 2, 10 and 16 are added to the 1st, 4th and 5th numbers respectively and 3 is subtracted from 2nd number then all 5 terms form an increasing arithmetic progression with common difference of 2. Which of the following is not a part of the series?
a) 13
b) 20
c) 7
d) 18
Download SSC GD FREE PREVIOUS PAPERS
Question 6: What is the value of least number that should be subtracted from 2550, so that the resultant is exactly divisible by 59?
a) 43
b) 13
c) 23
d) 19
Question 7: The ratio of two numbers is 4:7. If the square of the sum of both the numbers is 4356, then what is the difference between the square of the two numbers?
a) 941
b) 1376
c) 1188
d) 1296
Question 8: What is the value of
$\frac{\text{0.03 x 4.2 + 7.9 x 0.75 + 0.4 x 0.15} }{\text{3.2 x 0.06 + 3.75 x 0.4 + 3.03 x 0.45}}$ ?
a) 2
b) 3
c) 5
d) 7
Question 9: What is the value of $\frac{\text{0.02 x 4.2 + 7.9 x 0.5 + 0.4 x 0.1} }{\text{3.2 x 0.04 + 2.5 x 0.4 + 3.03 x 0.3}}$ ?
a) 1
b) 2
c) 3
d) 4
Question 10: If X = 28 * 47 * 89 * 14 * 46 * 32, what is the digit at unit’s place of X?
a) 2
b) 3
c) 6
d) 7
DOWNLOAD APP TO ACESS DIRECTLY ON MOBILE
Question 11: The LCM of two numbers is 5868 and their HCF is 26. What is the product of the two numbers?
a) 246758
b) 164628
c) 152568
d) 321448
Question 12: The ratio of two numbers is 6 : 7. If the GCD of these numbers is 4, what is their LCM?
a) 168
b) 174
c) 156
d) 192
Question 13: HCF of two numbers is 1/64th of their LCM. The sum of the HCF and LCM is 1105. If one number is 34, then what is the value of the other number?
a) 496
b) 488
c) 536
d) 544
Question 14: What is the sum of all prime numbers from 1 to 35?
a) 131
b) 129
c) 160
d) 141
Question 15: Calculate the total numbers of prime factors in the expression $(4)^{11} \times (5)^{5} \times (3)^{2} \times (13)^{2}$
a) 30
b) 31
c) 33
d) 32
Download SSC GD Constable Syllabus PDF
Question 16: Which of the following is NOT prime number?
a) 251
b) 571
c) 331
d) 341
Question 17: Find the number of prime factor of 1024.
a) 9
b) 10
c) 11
d) 12
Question 18: Calculate the total numbers of prime factors in the expression $(9)^{11} \times (5)^7 \times (7)^5 \times (3)^2 \times (17)^2$
a) 35
b) 36
c) 37
d) 38
Question 19: Find the number which is a prime number.
a) 39
b) 87
c) 79
d) 93
Question 20: Which of the following number is largest among all ?
$0.7,0.\overline{7},0.0\overline{7}0.\overline{07}$
a) $0.\overline{07}$
b) $0.0\overline{7}$
c) $0.7$
d) $0.\overline{7}$
Question 21: Find the number of prime factor of 20790.
a) 7
b) 9
c) 5
d) 13
Question 22: If a number 657423547X46 is divisible by 11, then find the value of X.
a) 7
b) 9
c) 8
d) 6
Question 23: Sum of four consecutive odd numbers is 208. Find the largest number.
a) 55
b) 57
c) 59
d) 61
Question 24: Find the sum of 0.99995 + 0.88885 + 0. 77775 + 0.66665 +0.55555
a) 3.88875
b) 2.88875
c) 3.6875
d) 2.9875
Question 25: A number is divided by 52, we get 27 as remainder. On dividing the same number by 13, What will be the remainder?
a) 2
b) 7
c) 1
d) None of these
Question 26: Find the smallest 8 digit number which is exactly divisible by 121.
a) 10000045
b) 10000076
c) 10000024
d) 10000055
100+ Free GK Tests for SSC Exams
Question 27: Find the number which is NOT a prime number.
a) 89
b) 87
c) 79
d) 97
Question 28: Find the unit place digit in 71 x 72 x 73 x 74 x 76 x 77 x 78 x 79.
a) 2
b) 0
c) 4
d) 6
Question 29: Find the number that is as much greater than 49 as is less than 95.
a) 23
b) 55
c) 72
d) 76
Question 30: The length of a string is 8 feet and 9 inches, which is divided into 3 equal parts. What is the length of each part in inches?
a) 31
b) 33
c) 35
d) 37
Question 31: How many 3 digit numbers are completely divided by 4.
a) 225
b) 224
c) 223
d) 222
Question 32: If 49 is subtracted from the square of a number, then the result obtained is 576. What is the number?
a) 24
b) 25
c) 23
d) 27
Question 33: What is the reminder, when $4x^{2}\div 10x^{2}-20x^{2}\div 90$ is divided by $(x\div2)$ ?
a) 0
b) 6
c) 45
d) 90
Question 34: The ratio of two numbers is 2:7. If the product of the numbers is 896, what is the difference between the square of the two numbers?
a) 1496
b) 2880
c) 2205
d) 1620
Question 35: The least number that should be added to 1375, so that the sum is exactly divisible by 29 is
a) 16
b) 21
c) 17
d) 18
Question 36: 5 दोस्तों P, Q, R, S, T एक इमारत की 1 से 5 तक मंजिलों पर रह रहे हैं, 1 सबसे नीची मंजिल है। T और R के बीच 2 व्यक्ति रहे हैं। R,T के एक मंजिल ऊपर रहता है। R सबसे शीर्ष पर मंजिल पर नहीं रहता है। S,P के एक मंजिल ऊपर रहता है लेकिन Q के नीचे । मंजिल 3 पर कौन रहता है?
a) S
b) P
c) Q
d) R
Question 37: Which of the following numbers represents decimal, octal & hexadecimal ?
a) 45654
b) 56789
c) 789A3
d) 845B6
Question 38: Convert 1101010 into octal system ?
a) 156
b) 154
c) 152
d) 150
Question 39: Convert 1101110 into decimal system ?
a) 104
b) 106
c) 108
d) 110
Question 40: Convert 234 into binary system ?
a) 11100100
b) 11101010
c) 11100110
d) 11101110
Answers & Solutions:
1) Answer (D)
We have to find out 25% of 48 + 50% of 120 + 70% of 75 + 14% of 45
$\Rightarrow$ $\frac{25}{100}\times 48 + \frac{50}{100}\times 120 + \frac{70}{100}\times 75 + \frac{14}{100}\times 45$
$\Rightarrow$ $12 + 60 + 52.50 + 6.30$
$\Rightarrow$ $130.8$
Let us assume that x is the missing number.
Therefore x = $\frac{130.8}{327}\times 100$ = 40
Hence option D is the correct answer.
2) Answer (D)
Let the numbers be $5x$ and $13x$.
We have $5x*13x = 65x^2 = 3185$
$\Rightarrow$ $x^2 = 49$
Difference sum the squares of the two numbers = $(5x)^2 + (13x)^2$ = $194 x^2$
$\Rightarrow$ $194*49$
$\Rightarrow$ $9506$
So, option D is the right choice.
3) Answer (C)
The units digit of $7^{79}$ is same as the units digit of $7^{3}$ as the cyclicity of 7 is 4.
$7^{3} = 343$
The units digit of $13^{62}$ is same as the units digit of $3^{62}$ which, in turn, same as the unit digit of $3^{2}$ as the cyclicity of 3 is 4.
$3^{2} = 9$
The units digit of $7^{79}+13^{62}$ is the units digit of the sum 7+9
$3 + 9 = 12$
Therefore 2 is the unit digit of the given expression. Hence, option C is the correct answer.
4) Answer (D)
The difference between the divisors and the respective remainders is 1 in each case. So, the least number is is given by finding the LCM of all the divisors and subtracting 1 from it.
Least no. = LCM – 1 = 60 – 1 = 59
Hence, option D is the correct answer.
5) Answer (D)
Let us assume that numbers are $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$.
$\Rightarrow$ $a_{1}+a_{2}+a_{3}+a_{4}+a_{5} = 70$
Term of an arithmetic progression $a_{1}+2, a_{2}-3, a_{3}, a_{4}+10$ and $a_{5}+16$
Sum of all terms of the A.P. = $(a_{1}+2)+(a_{2}-3)+(a_{3})+(a_{4}+10)+(a_{5}+16)$
$\Rightarrow$ $\Large\frac{5}{2}$ $\times$ $(2A+[5-1]2)$ = $ (a_{1}+a_{2}+a_{3}+a_{4}+a_{5})+25$ (Where A is the 1st term of the arithmetic progression)
$\Rightarrow$ $\Large\frac{5}{2}$ $\times$ $(2A+8) = 70+25$
$\Rightarrow$ $5A+20 = 95$
$\Rightarrow$ $A = 15$
So the A.P. will be = $(15, 17, 19, 21, 23)$ = ($a_{1}+2, a_{2}-3, a_{3}, a_{4}+10$ and $a_{5}+16$)
Therefore $a_{1} = 15 – 2 = 13$
Similarly $a_{2} = 17 + 3 = 20$
$a_{3} = 19$
$a_{4} = 21 – 10 = 11$
$a_{5} = 23 – 16 = 7$
Hence we can say that the numbers are $(13, 20, 19, 11, 7)$. We can see that 18 is not a part of this set therefore option D is the correct answer.
6) Answer (B)
The remainder obtained by dividing 2550 by 59
$\Rightarrow$ $Rem.(\frac{2550}{59}) = 13$
Hence we can say that we should subtract 13 from 2550 so that resultant will be divisible by 59. Hence option B is correct answer.
7) Answer (C)
Let us assume the numbers to be $4x, 7x$.
It is given that the square of sum of these numbers
$\Rightarrow$ $(4x +7x)^2 = 4356$
$\Rightarrow$ $121x^2 = 4356$
$\Rightarrow$ $x^2 = 36$ … (1)
The difference between the squares of these two numbers
$\Rightarrow$ $(7x)^2 – (4x)^2$
$\Rightarrow$ $33x^2$
$\Rightarrow$ $33\times 36 = 1188$
Hence option C is the correct answer.
8) Answer (A)
$\frac{\text{0.03 x 4.2 + 7.9 x 0.75 + 0.4 x 0.15} }{\text{3.2 x 0.06 + 3.75 x 0.4 + 3.03 x 0.45}}$
=$\frac{\text{0.126 + 5.925 + 0.06}}{\text{0.192 + 1.5+ 1.3635}}$
=$\frac{6.1110}{3.0555}$
= 2
Hence, the option A is correct.
9) Answer (B)
$\frac{\text{0.02 x 4.2 + 7.9 x 0.5 + 0.4 x 0.1} }{\text{3.2 x 0.04 + 2.5 x 0.4 + 3.03 x 0.3}}$
=$\frac{\text{0.084 + 3.95 + 0.04}}{\text{0.128 + 1 + 0.909}}$
=$\frac{4.074}{2.037}$
= 2
Hence, option B is correct.
10) Answer (A)
To find out the unit digit we can check the product of digits at unit place of all the numbers.
8 * 7 = 56
6 * 9 = 54
4 * 4 = 16
6 * 6 = 36
6 * 2 = 12
So, the digit at unit’s place is 2. Hence, option A is correct.
11) Answer (C)
We know that product of two numbers is equal to the product of their LCM and HCF.
So, the product of the numbers = 5868 * 26 = 152568
Hence, option C is correct.
12) Answer (A)
Let the two numbers be 6x and 7x.
Since the HCF of two numbers is 4, x = 4
The two numbers are 24 and 28.
LCM = 6 * 7 * 4 = 168
Hence, option A is the right choice.
13) Answer (D)
Let the HCF of the two numbers be ‘h’.
Thus, the LCM will be 64h.
LCM + HCF = 1105
h + 64h = 1105
h = HCF = 17
LCM = 64*17
HCF*LCM = Product of the two numbers
17 * 64 *17 = 34 * x
x = 544
Hence, option D is the right choice.
14) Answer (C)
Prime numbers from 1 to 35 = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31}
Therefore, the sum of all prime numbers from 1 to 35 is 2+3+5+7+11+13+17+19+23+29+31 = 160
Therefore, option C is the right answer.
15) Answer (B)
Expression : $(4)^{11} \times (5)^{5} \times (3)^{2} \times (13)^{2}$
Prime factorization = $(2)^{22} \times (5)^{5} \times (3)^{2} \times (13)^{2}$
Now, there are 4 distinct factors = $2,3,5,13$
Total number of prime factors = $22+5+2+2=31$
=> Ans – (B)
16) Answer (D)
Prime factors of 341 = 11 and 31
Hence, among the given numbers, 341 is not prime.
=> Ans – (D)
17) Answer (B)
Prime factorisation of $1024=(2)^{10}$
Thus, number of prime factors = $10$
=> Ans – B
18) Answer (D)
Expression : $(9)^{11} \times (5)^7 \times (7)^5 \times (3)^2 \times (17)^2$
Prime factorization = $(3)^{22} \times (5)^{7}\times(7)^5 \times (3)^{2} \times (17)^{2}$
= $(3)^{24} \times (5)^{7}\times(7)^5 \times (17)^{2}$
Now, there are 4 distinct factors = $3,5,7,17$
Total number of prime factors = $24+7+5+2=38$
=> Ans – (D)
19) Answer (C)
39, 87 and 93 are divisible by 3, hence are composite.
Only 79 is a prime number among the given options.
=> Ans – (C)
20) Answer (D)
Terms : $0.7,0.\overline{7},0.0\overline{7}0.\overline{07}$
We know that $0.n>0.0n$, where $n$ is any one digit number.
Also, $0.77>0.70$, => $0.\overline{7}>0.7$
$\therefore$ $0.\overline{7}$ is the largest.
=> Ans – (D)
21) Answer (C)
Prime factorisation of $20790=(2)^1\times(3)^3\times(5)^1\times(7)^1\times(11)^1$
Thus, number of prime factors = $5$
=> Ans – (C)
22) Answer (B)
For a number $657423547X46$ to be divisible by 11, the difference between the sum of numbers at even position and odd position should be either ‘0’ or ’11’.
Sum of digits at odd position (starting from right) = $6+X+4+3+4+5=(22+X)$
Even positions = $4+7+5+2+7+6=31$
=> $22+X-31=0$
=> $X=9$
=> Ans – (B)
23) Answer (A)
Let the four consecutive odd numbers be $(x-3),(x-1),(x+1)$ and $(x+3)$
Sum = $(x-3)+(x-1)+(x+1)$ $+(x+3)=208$
=> $4x=208$
=> $x=\frac{208}{4}=52$
$\therefore$ Largest number = $52+3=55$
=> Ans – (A)
24) Answer (A)
Expression : 0.99995 + 0.88885 + 0. 77775 + 0.66665 + 0.55555
= 3.88875
=> Ans – (A)
25) Answer (C)
When a number is divided by 52, remainder obtained is 27,
=> Number is of the form = $52k+27$
When above number is divided by 13, => $\frac{(52k+27)}{13}$
$\because$ 52 is a multiple of 13, => $27\%13=1$
=> Ans – (C)
26) Answer (A)
Smallest 8 digit number = 10000000
If we divide above number by 121, remainder is = $10000000 = 121\times82644+76$
=> Smallest 8 digit number which is exactly divisible by 121 = $10000000+(121-76)=10000045$
=> Ans – (A)
27) Answer (B)
Prime factors of 87 = 3 and 29
Hence, among the given numbers, 87 is not prime.
=> Ans – (B)
28) Answer (D)
Expression : 71 x 72 x 73 x 74 x 76 x 77 x 78 x 79
Unit place is the product of unit digits.
= $(1\times2\times3\times4)\times(6\times7)\times(8\times9)$
= $24\times42\times72$
$\equiv4\times2\times2=16$
Thus, unit digit = 6
=> Ans – (D)
29) Answer (C)
Number that is as much greater than 49 as is less than 95 is the average of both 49 and 95
=> Average = $\frac{(49+95)}{2}$
= $\frac{144}{2}=72$
=> Ans – (C)
30) Answer (C)
1 feet = 12 inches
Length of string = 8 feet 9 inches = $8\times12+9=105$ inches
=> Length of each part = $\frac{105}{3}=35$ inches
=> Ans – (C)
31) Answer (A)
3 digit numbers that are divided by 4 are : 100,104,108,…………….,992,996
Above series is an A.P. with first term, $a=100$, common difference, $d=4$ and last term, $l=996$
Thus, $n^{th}$ term of an A.P., $A_n=a+(n-1)d$
=> $100+(n-1)4=996$
=> $(n-1)\times4=996-100=896$
=> $(n-1)=\frac{896}{4}=224$
=> $n=224+1=225$
$\therefore$ There are 225 three digit numbers that are divided by 4.
=> Ans – (A)
32) Answer (B)
Let the number be $x$
According to ques,
=> $x^2-49=576$
=> $x^2=576+49=625$
=> $x=\sqrt{625}=25$
=> Ans – (B)
33) Answer (B)
34) Answer (B)
Let the numbers be 2x and 7x.
We have $2x*7x = 14x^2$ = 896
x = 8
So, the two numbers are 2*8 and 7*8 i.e 16 and 56.
Difference between the squares of the 2 numbers = $56^2 – 16^2$ = 3136 – 256 = 2880.
So, option B is the right choice.
35) Answer (C)
The remainder obtained by dividing 1375 by 29 is 12
So, the least number that should be added to 1375 to make it perfectly divisible by 29 is 29 – 12 = 17.
Therefore, option C is the right answer.
36) Answer (A)
R मंजिल 4 पर रहना चाहिए क्योंकि T और R के बीच 2 व्यक्ति रहते हैं, T, R से ऊपर पर रहता है और R सबसे शीर्ष मंजिल पर नहीं रहता है। T को मंजिल 1 पर रहना चाहिए. S ,P से एक मंजिल ऊपर रहता है लेकिन Q से नीचे।
इसलिए, S मंजिल 3 पर रहना चाहिए, P मंजिल 2 पर रहना चाहिए और Q फर्श 5 पर रहना चाहिए। इसलिए उत्तर A है।
37) Answer (A)
56789 has ‘9’ so it doesnt represent octal system
789A3 has ‘A’ so it represents only hexa decimal system
845B6 has ‘B’ so it represents only hexa decimal system
456564 represents all decimal octal and hexa decimal systems
So the answer is option A.
38) Answer (C)
1101010 = 001 101 010
$001 = 0(2^2)+0(2^1)+1(2^0) = 1$
$101 = 1(2^2)+0(2^1)+1(2^0) = 5$
$010 = 0(2^2)+1(2^1)+0(2^0) = 2$
$(1101010)_2 = (152)_8$
So the answer is option C.
39) Answer (D)
$(1101110)_2 = 1(2^6)+1(2^5)+0(2^4)+1(2^3)+1(2^2)+1(2^1)+0(2^0) = 64+32+0+8+4+2+0 = (110)_{10}$
So the answer is option D.
40) Answer (B)
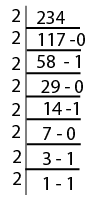
$(234)_{10} = (11101010)_2$
So the answer is option B.
Download SSC GD Previous Papers PDF
DOWNLOAD APP FOR SSC FREE MOCKS
We hope this Number System questions for SSC GD will be highly useful for your preparation.





