Line Graphs Questions for NMAT – Download [PDF]
Download Line Graphs Questions for NMAT PDF. Top 10 very important Line Graphs Questions for NMAT based on asked questions in previous exam papers.
Download Line Graphs Questions for NMAT
Take NMAT mock test
Question 1: The area, in sq. units, enclosed by the lines $x=2,y=\mid x-2\mid+4$, the X-axis and the Y-axis is equal to
a) 10
b) 6
c) 8
d) 12
Question 2: Determine the value(s) of “a” for which the point $(a, a^{2})$ lies inside the triangle formed by the lines: 2x+ 3y= 1, x+ 2y=3 and 5x-6y= 1
a) (-3,-1) ⋃ (1/2, 1)
b) (-∞, 1/3) ⋃ (1/2, ∞)
c) (-3/2,-1) ⋃ (1/2, 1)
d) (-∞, 1) ⋃ (1/3, 6)
e) None of the above
Question 3: When the curves $y = log_{10}x$ and $y = x^{-1}$ are drawn in the x-y plane, how many times do they intersect for values $x \geq 1$ ?
a) Never
b) Once
c) Twice
d) More than twice
Question 4: In the X-Y plane, the area of the region bounded by the graph of |x+y| + |x-y| = 4 is
a) 8
b) 12
c) 16
d) 20
Question 5: The graph of y – x (on the y axis) against y + x (on the x axis) is as shown below. (All graphs in this question are drawn to scale and the same scale and the same scale has been used on each axis.)
Which of the following shows the graph of y against x?
a)
b)
c)
d)
Question 6: The number of real-valued solutions of the equation $2^{x}+2^{-x}=2-(x-2)^{2}$ is:
a) 1
b) 2
c) infinite
d) 0
Question 7: The figure below shows the graph of a function f(x). How many solutions does the equation f(f(x)) = 15 have?
a) 5
b) 6
c) 7
d) 8
e) cannot be determined from the given graph
Question 8: Find the equation of the graph shown below.
a) y = 3x – 4
b) y = $2x^{2}$ – 40
c) x = $2y^{2}$ – 40
d) y = $2x^{2}$ + 3x – 19
e) x = $2y^{2}$ + 3x – 19
Question 9: Let g(x) = max(5 – x, x + 2). The smallest possible value of g(x) is
a) 4.0
b) 4.5
c) 1.5
d) None of the above
Question 10: The area bounded by the three curves |x+y| = 1, |x| = 1, and |y| = 1, is equal to:
a) 4
b) 3
c) 2
d) 1
Join 7K MBA Aspirants Telegram Group
Download Highly Rated CAT preparation App
Answers & Solutions:
1) Answer (A)
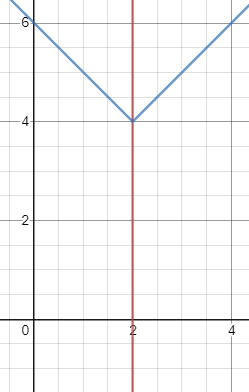
The required figure is a trapezium with vertices A(0,0), B(2,0), C(2,4) and D(0,6)
AB = 2 BC = 4 and AD = 6
Area of trapezium = $\frac{1}{2}\left(sum\ of\ the\ opposite\ sides\right)\cdot height$ = $\frac{1}{2}\left(4+6\right)\cdot2\ =\ 10$
2) Answer (C)
Let us draw the diagram first,
Let L$_{1}$: 2x+ 3y -1 = 0
L$_{2}$: x+ 2y -3 = 0
L$_{3}$: 5x-6y- 1 = 0
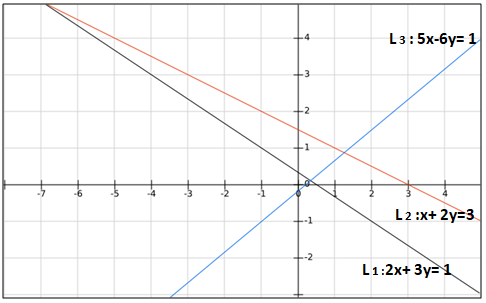
With respect to L$_{1}$, we can see that the point $(a, a^{2})$ lies within the triangle and (0, 0) are opposite side. Therefore,
L$_{(a, a^2)}$* L$_{(0, 0)}$ < 0
$\Rightarrow$ $(2a+ 3a^2-1)(-1)<0$
$\Rightarrow$ $(3a^2+2a-1)>0$
$\Rightarrow$ a < -1 or a > $\frac{1}{3}$ … (1)
With respect to L$_{2}$, we can see that the point $(a, a^{2})$ lies within the triangle and (0, 0) are on the same side. Therefore,
L$_{(a, a^2)}$* L$_{(0, 0)}$ > 0
$\Rightarrow$ $(a+ 2a^2-3)(-3)>0$
$\Rightarrow$ $(2a^2+a-3)<0$
$\Rightarrow$ $\frac{-3}{2}$ < a < 1 … (2)
With respect to L$_{3}$, we can see that the point $(a, a^{2})$ lies within the triangle and (0, 0) are on the same side. Therefore,
L$_{(a, a^2)}$* L$_{(0, 0)}$ > 0
$\Rightarrow$ $(5a- 6a^2-1)(-1)>0$
$\Rightarrow$ $(6a^2-5a+1)>0$
$\Rightarrow$ a < $\frac{1}{3}$ or a > $\frac{1}{2}$ … (3)
From equation (1), (2) and (3) we can say that
a $\epsilon$ (-3/2,-1) ⋃ (1/2, 1). Hence, option C is the correct answer.
3) Answer (B)
Graph of logx goes on increasing in 1st quadrant and graph of 1/x goes no decreasing with both intersecting only once
4) Answer (C)
If the moduli are removed, the equations formed are
x+y+x-y = 4 => x=2
x+y-x+y = 4 => y =2
-x-y+x-y = 4 => y=-2
-x-y-x+y = 4 => x=-2
The area enclosed by these equations is a square with vertices at (2,2), (-2,2), (-2,-2), (2,-2) as shown in figure.
The required area = 4*4 = 16
5) Answer (D)
For a normal graph with y and x-axis, the equation of the line passing through the origin is y =mx where m is the slope of the line.
m is +ve if the angle made by the line with the x-axis is < $90^{\circ\ }$
$\therefore\ $ The equation of the line in the given graph would be y-x = k( y+ x) since the axes are y-x and y+x and the line is passing through the origin.
k > 1 because the angle is greater than 45$^{\circ\ }$
$y=\frac{k\left(x+1\right)}{1-k}$
Since k>1
Therefore y<0 for x>-1 and y>0 for x<-1
Option d correctly satisfy this condition
6) Answer (D)
The graphs of $2^{x}+2^{-x} and 2-(x-2)^{2}$ never intersect. So, number of solutions=0.
Alternate method:
We notice that the minimum value of the term in the LHS will be greater than or equal to 2 {at x=0; LHS = 2}. However, the term in the RHS is less than or equal to 2 {at x=2; RHS = 2}. The values of x at which both the sides become 2 are distinct; hence, there are zero real-valued solutions to the above equation.
7) Answer (C)
It has been given that f(f(x)) = 15.
From the graph, we can see that the value of f(4) = 15 and f(12) = 15
Therefore, f(x) can be 4 or 12.
When f(x) = 4, x can take 4 values
When f(x) = 12, x can take 3 values.
Therefore, there are 4+3 = 7 solutions in total.
Therefore, option C is the right answer.
8) Answer (D)
When x = -3, y = -10
This is satisfied only in option D.
Hence, option D is the correct answer.
9) Answer (D)
Smallest possible value would be at 5-x = x+2 i.e. x= 1.5 as shown
Substituting we get smallest value as 3.5.
10) Answer (B)
|x| = 1 and |y| = 1 form a square of area = 2*2 = 4 sq units
|x+y| = 1 forms a set of parallel lines cutting the axes at (1,0), (0,1), (-1,0) and (0,-1). The graph is as shown:
The area bounded by the three curves is 2*2 – 1/2*1*1*2 = 4 – 1 = 3 sq units
We hope this Line Graphs Questions for NMAT pdf for NMAT exam will be highly useful for your Preparation.
