Geometry Questions for XAT 2022 – Download [PDF]

Download Geometry Questions for XAT PDF – XAT Geometry questions pdf by Cracku. Top 10 very Important Geometry Questions for XAT based on asked questions in previous exam papers.

Download Geometry Questions for XAT

Get 5 XAT mocks at just Rs.299

Question 1: There is a triangular building (ABC) located in the heart of Jaipur, the Pink City. The length of the one wall in east (BC) direction is 1500 feet. If the length of south wall (AB) is perfect cube, the length of southwest wall (AC) is a power of three, and the length of wall in southwest (AC) is thrice the length of side AB, determine the perimeter of this triangular building.

a) 4209 feet

b) 4213 feet

c) 4773 feet

d) 4416 feet

Question 2: There are two buildings, one on each bank of a river, opposite to each other. From the top of one building – 60 m high, the angles of depression of the top and the foot of the other building are 30° and 60° respectively. What is the height of the other building?

a) 30 m

b) 18 m

c) 40 m

d) 20 m

Question 3: Consider the volumes of the following objects and arrange them in decreasing order:
i. A parallelepiped of length 5 cm, breadth 3 cm and height 4 cm
ii. A cube of each side 4 cm.
iii. A cylinder of radius 3 cm and length 3 cm
iv. A sphere of radius 3 cm

a) iv,iii,ii,i

b) iv,ii,iii,i

c) iv,iii,i,ii

d) None of the above

Question 4: The area of a triangle is 6, two of its vertices are (1, 1) and (4, -1), the third vertex lies on y = x + 5. Find the third vertex.

a) $(\frac{2}{5},\frac{27}{5})$

b) $(-\frac{3}{5},\frac{22}{5})$

c) $(\frac{3}{5},\frac{28}{3})$

d) None of these

Question 5: Mohan was playing with a square cardboard of side 2 metres. While playing, he sliced off the corners of the cardboard in such a manner that a figure having all its sides equal was generated. The area of this eight sided figure is:

a) $\frac{4\sqrt{2}}{(\sqrt{2}+1)}$

b) $\frac{4}{(\sqrt{2}+1)}$

c) $\frac{2\sqrt{2}}{(\sqrt{2}+1)}$

d) $\frac{8}{(\sqrt{2}+1)}$

XAT 2022 Crash Course

Instructions

Based on the following information

A man standing on a boat south of a light house observes his shadow to be 24 meters long, as measured at the sea level. On sailing 300 meters eastwards, he finds his shadow as 30 meters long, measured in a similar manner. The height of the man is 6 meters above sea level.

Question 6: The height of the light house above the sea level is:

a) 90 meters

b) 94 meters

c) 96 meters

d) 100 meters

e) 106 meters

Question 7: The centre of a circle inside a triangle is at a distance of 625 cm. from each of the vertices of the triangle. If the diameter of the circle is 350 cm. and the circle is touching only two sides of the triangle, find the area of the triangle.

a) 240000

b) 387072

c) 480000

d) 506447

e) None of the above

Question 8: Let $S_{1}, S_{2},…$ be the squares such that for each n ≥ 1, the length of the diagonal of $S_{n}$ is equal to the length of the side of $S_{n+1}$. If the length of the side of $S_{3}$ is 4 cm, what is the length of the side of $S_{n}$ ?

a) $2^[{\frac{2n+1}{2}}]$

b) $2.(n-1)$

c) $2^{n-1}$

d) $2^[{\frac{n+1}{2}}]$

e) None of these

Question 9: A circle circumscribes a square. What is the area of the square?I. Radius of the circle is given.II. Length of the tangent from a point 5 cm away from the centre of the circle is given.

a) The question can be answered with the help of any one statement alone but not by the other statement.

b) The question can be answered with the help of either of the statements taken individually.

c) The question can be answered with the help of both statements together.

d) The question cannot be answered even with the help of both statements together.

Question 10: The figure shows the rectangle ABCD with a semicircle and a circle inscribed inside in it as shown. What is the ratio of the area of the circle to that of the semicircle?

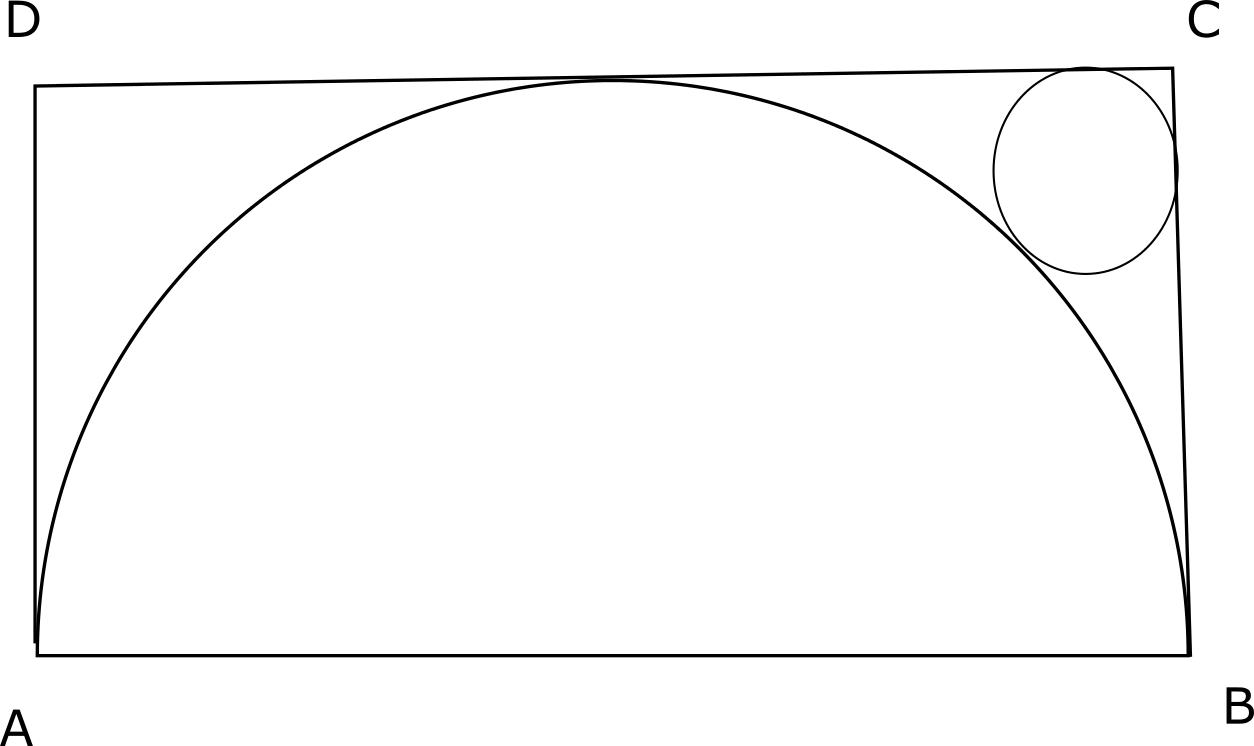
a) $(\sqrt2 -1)^{2}:1$

b) $2(\sqrt{2} -1)^2 :1$

c) $(\sqrt2-1)^2 :2$

d) None of these

Take XAT 2022 mocks

Answers & Solutions:

1) Answer (D)

The given condition is as shown below:-

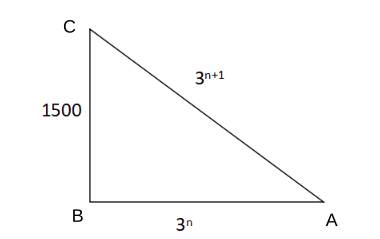
Now, $3^n, 3^{n+1}$ pairs are (1,3), (27,81), (729, 2187) and so on
1500, 3 and 397 cannot form a triangle
1500, 81 and 397 cannot form  triangle
1500, 729 and 2187 can form a triangle
Thus, the perimeter of the building = 1500+729+2187 = 4416 feet
Hence, option D is the correct answer.

2) Answer (C)

The given situation is as shown:-

Width of the river = tan 30 * 60 = 20$\sqrt3$
Now Tan 30 = (60-x)/(20$\sqrt3$)
Solving we get x = 40m
Thus, the height of the building = 40m
Hence, option C is the correct answer.

3) Answer (A)

i. Volume of the parallelepiped of length 5 cm, breadth 3 cm and height 4 cm = 3*4*5 = 60 cm$^3$
ii. Volume  of the cube of each side 4 cm = 4^3 = 64 cm$^3$
iii.Volume  of the cylinder of radius 3 cm and length 3 cm = $\pi*3^2*3$ = 84.82 cm$^3$
iv. Volume  of the  sphere of radius 3 cm = $4/3*\pi*3^3$ = 113.09 cm$^3$

Therefore, we can say that volumes of the objects in decreasing order = iv,iii,ii,i.

Hence, option A is the correct answer.

4) Answer (A)

Let us assume that X co-ordinate of the 3rd vertex is a. Then y = a + 5. So the co-ordinates of the vertex = (a, a+5)

Ttherefore, 6 =   $\dfrac{1}{2}\times \begin{vmatrix}1 & 1 & 1\\4 & -1 & 1\\a & a+5 & 1 \end{vmatrix}$

$\Rightarrow$ $\pm12$ = 1(-1-a-5) -1(4 – a) + 1(4a+20+a)
$\Rightarrow$ $\pm12$ = 5a + 10
$\Rightarrow$ a = $\dfrac{2}{5}$, $\dfrac{-22}{5}$

Hence, the third vertex can be out of the two values ($\dfrac{2}{5}$, $\dfrac{27}{5}$) or ($\dfrac{-22}{5}$, $\dfrac{3}{5}$).

Therefore, option A is the correct answer.

5) Answer (D)

We can see that we will get a regular octagon as shown in the figure below.

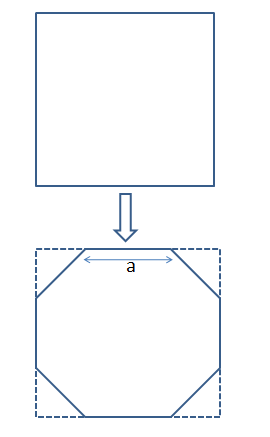
Let ‘a’ be the length of the side of the regular octagon.

Hence, we can say that, $\dfrac{a}{\sqrt{2}}+a+\dfrac{a}{\sqrt{2}} = 2$

$\Rightarrow$ $a = \dfrac{2}{\sqrt{2}+1}$.

Area of a regular octagon = $2*(1+\sqrt{2})*a^2$

$\Rightarrow$ $2*(1+\sqrt{2})*(\dfrac{2}{\sqrt{2}+1})^2$

$\Rightarrow$ $\dfrac{8}{(\sqrt{2}+1)}$.

Therefore, option D is the correct answer.

6) Answer (E)

KL = lighthouse

BA = initial position man of man and BC = shadow

After moving 300 m east, DE = new position of man and EF = shadow

Given : AB = DE = 6 m

BC = 24 m and EF = 30 m and BE = 300 m

$\triangle$ LBE is right angled triangle (sea level).

To find : KL = ?

Solution : In $\triangle$ KLF and $\triangle$ DEF

=> $\angle KLF = \angle DEF = 90$

$\angle KFL = \angle DFE$ (common angle)

=> $\triangle KLF \sim \triangle DEF$

=> $\frac{KL}{DE} = \frac{LF}{EF}$ ———–Eqn(I)

Similarly, $\triangle KLC \sim \triangle ABC$

=> $\frac{KL}{AB} = \frac{LC}{BC}$ ———-Eqn(II)

From eqn (I) and (II), and using AB = DE

=> $\frac{LC}{BC} = \frac{LF}{EF}$

=> $\frac{LC}{24} = \frac{LF}{30}$

=> $\frac{LC}{LF} = \frac{24}{30} = \frac{4}{5}$

If, LC is 4 part $\equiv$ LF is 5 part

=> $LB = 4x$ and $LE = 5x$

$\because$ $\triangle$ LBE is right angled triangle

=> $(LE)^2 – (LB)^2 = (BE)^2$

=> $25X^2 – 16X^2 = 90000$

=> $x^2 = \frac{90000}{9} = 10000$

=> $x = \sqrt{10000} = 100$

=> $LB = 400$ and $LE = 500$

=> $LC = LB + BC = 400 + 24 = 424$

Now, using Eqn (II), we get :

=> $KL = \frac{LC}{BC} \times AB$

= $\frac{424}{24} \times 6 = \frac{424}{4}$

= $106 m$

7) Answer (B)

If a point is equidistant from all 3 vertices, it has to be the circumcentre. The given circle with centre S is concentric and touches two sides.

As S is equidistant from 2 of the sides (say AB and AC), => It lies on angle bisector of $\angle A$.

=> $\triangle ABC$ is isosceles with AB = AC

Radius of the circle = RS = SQ = 175 cm and SA = SB = SC = 625 cm

=> $AR = \sqrt{625^2 – 175^2} = 600$

Let SP = x

=> $(BP)^2 = (BA)^2 – (AP)^2 = (BS)^2 – (SP)^2$

=> $1200^2 – (625 + x)^2 = 625^2 – x^2$

=>$1200^2 – 625^2 – x^2 – 2*625x = 625^2 – x^2$

=> $1200^2 – 2 * 625^2 = 1250x$

=> $x = \frac{658750}{1250} = 527$

=> $BP = \sqrt{625^2 – 527^2} = 336$

$\therefore$ ar $(\triangle ABC)$ = $\triangle ASB + \triangle ASC + \triangle SBC$

= $(600 \times 175) + (600 \times 175) + (527 \times 336)$

= $105000 + 105000 + 177072 = 387072$

8) Answer (D)

Length of side of $S_{n + 1}$ = Length of diagonal of $S_n$

=> Length of side of $S_{n + 1}$ = $\sqrt{2}$ (Length of side of $S_{n}$)

=> $\frac{\textrm{Length of side of }S_{n + 1}}{\textrm{Length of side of }S_n} = \sqrt{2}$

=> Sides of $S_1 , S_2 , S_3 , S_4,…….., S_n$ form a G.P. with common ratio, $r = \sqrt{2}$

It is given that, $S_3 = ar^2 = 4$

=> $a (\sqrt{2})^2 = 4$

=> $a = \frac{4}{2} = 2$

$\therefore$ $n^{th}$ term of G.P. = $a (r^{n – 1})$

= $2 (\sqrt{2})^{n – 1}$

=$2^[{\frac{n+1}{2}}]$

9) Answer (B)

As the circle circumscribes the square, diameter of the circle= diagonal of the square. Let the side of the circle be s. If we can determine the value of s, then we can find the area of the square $s^2$.

Statement 1: Let the radius be r. 2r = $s \sqrt{2}$. Hence, s = $r\sqrt{2}$. Thus, we can find the area of the circle using this information.

Statement 2: This scenario can be drawn as shown below:

A line drawn from the center of the circle intersects the tangent at an angle of 90°. Hence, the triangle formed is a right-angled triangle with the hypotenuse of 5 cm, one side equal to the radius of the circle and second side equal to the length of the tangent. If the length of the tangent is known then we can calculate the radius using Pythogoras theorem. If the radius is known, the area of the square can be calculated as shown above.

10) Answer (D)

Let the center be O and the point at which the semicircle intersects CD be P.

Let the radius of the semicircle be R and the circle be r.

OP = R and OC = R$\sqrt{2}$

OC – OT = CC’ – TC’

$R\sqrt{2} – R – 2r$ = $r\sqrt{2} – r$

=> $R\sqrt{2} – R$ = $r\sqrt{2} + r$

=> r = $\frac{(\sqrt{2}-1)R}{\sqrt{2}+1}$

=> r = $(\sqrt{2}-1)^2$R

Ratio of areas will be $r^2 : \frac{R^2}{2}$ = $2(\sqrt{2}-1)^4$ : 1

Download XAT previous papaers [PDF]

We hope these geometry questions for XAT pdf for the XAT exam will be highly useful for your preparation.