Coordinate Geometry Questions for SSC GD PDF Set – 2
SSC GD Constable Coordinate Geometry Question paper with answers download PDF based on SSC GD exam previous papers. 40 Very important Coordinate Geometry questions for GD Constable.
Download COORDINATE GEOMETRY SSC GD QUESTIONS SET – 2 PDF
GET 20 SSC GD MOCK FOR JUST RS. 117
Download SSC GD Important Questions PDF
1500+ Must Solve Questions for SSC Exams (Question bank)
Question 1: The coordinates of the vertices of a right angled triangle are A(2,3) B(8,3) and C(2, -2). The triangle is right angled at A. Find the orthocenter of the triangle ABC ?
a) (2,-2)
b) (8,3)
c) (6,3)
d) (2,3)
Question 2: What is the equation of a circle of radius 4 units centered at (1, 2) ?
a) $x^2+y^2-2x-4y+5=0$
b) $x^2+y^2-2x-4y-11 = 0$
c) $x^2+y^2+2x-4y-11 = 0$
d) $x^2+y^2-2x+4y-11 = 0$
Question 3: What is the reflection of the point ( -4, 2) in the line x = -3?
a) (-2, -2)
b) (-2, 2)
c) (1, -2)
d) (1, 2)
Question 4: Find the slope of the line joining A(5,-1) & B(2, 2) ?
a) 1
b) -1
c) 2
d) -2
Question 5: Point P is the midpoint of segment AB. Coordinates of P are (-1 , -1) and B are (-5, -4) What are the coordinates of point A?
a) (3,-2)
b) (-3,-2)
c) (3,2)
d) (-3,2)
Download SSC GD FREE PREVIOUS PAPERS
Question 6: In what ratio does the point T(x,3) divide the segment joining the points S(3, -1) and U(-1, 2)?
a) 4:1
b) -4:1
c) 1:4
d) -1:4
Question 7: What is the reflection of the point (-4 , 3) in the line x = -1?
a) (-2 , 3)
b) (2 , -3)
c) (-2 , -3)
d) (2 , 3)
Question 8: At what point does the line 3x – 2y = 12 intersect the Y-axis?
a) (0,-6)
b) (-6,0)
c) (0,6)
d) (6,0)
Question 9: Find the slope of the line parallel to x-3y+2=0 ?
a) -1/3
b) 1/3
c) 3
d) -3
Question 10: Find the point which divides the line joining A(2,3) B(4,1) in the ratio 2:3 internally?
a) (-14/5, -11/5)
b) (14/5, -11/5)
c) (-14/5, 11/5)
d) (14/5, 11/5)
DOWNLOAD APP TO ACESS DIRECTLY ON MOBILE
Question 11: If P(x,2) is the centroid of the triangle formed by A(2,y), B(-1,-3) & C(2,6). Then find x*y ?
a) 13
b) 31
c) 3
d) -3
Question 12: What is the reflection of the point (-2,-2) in the line y = -1?
a) (-2 , 0)
b) (-2, -1)
c) (0 , -2)
d) (-2, 1)
Question 13: At what point does the line 3x + 2y = 12 cuts the X-axis?
a) (0,6)
b) (4,0)
c) (-4,0)
d) (0,-6)
Question 14: What is the slope of the line perpendicular to the line 2x+2y=3?
a) -2
b) 2
c) -1
d) 1
Question 15: Find the ratio in which P(3,Y) divides the line joining A(1,-3) and B(4,2) ?
a) 1:2
b) 2:1
c) -2:1
d) -1:2
Download SSC GD Constable Syllabus PDF
Question 16: Point P is the midpoint of segment AB. Coordinates of P are (2 , -1) and B are (5, -4) What are the coordinates of point A?
a) (-1, -2)
b) (-1, 2)
c) (1, 2)
d) (1, -2)
Question 17: What is the reflection of the point (-1 , 1) in the line y = 0?
a) (-2, 1)
b) (-2, -1)
c) (-1, -1)
d) (1, -1)
Question 18: What is the slope of the line perpendicular to the line passing through the points (-3 , 1) and (-2 , 2)?
a) 0
b) 1
c) -1
d) 2
Question 19: If P(1,2) is the centroid of the triangle formed by A(2,3), B(-1,-3) & C(x,y). Then find x-y ?
a) -4
b) 4
c) 3
d) -3
Question 20: In what ratio does the point T(1, y) divide the segment joining the points S(3, -1) and U(-1, 2)?
a) 2 : 1
b) 1 : 3
c) 3 : 2
d) 1 : 1
Question 21: What is the reflection of the point (4 , 3) in the line y = -1?
a) (4, 5)
b) (-4, 5)
c) (4, -5)
d) (-4, -5)
Question 22: Find the length of the median BE of a triangle ABC, with vertices A(1,2) , B(2,3) and C(3,6) ?
a) 1 unit
b) 2 units
c) 3 units
d) 4 units
Question 23: Find the slope of the line joining A(-1,2) and B(1, -2) ?
a) -2
b) 0
c) 2
d) undefined
Question 24: If P(2, 3) is the midpoint of A(4, y) and B(x, 1), then find x ?
a) 1
b) 2
c) 0
d) -1
Question 25: What is the reflection of the point ( 2, -2) in the line y = -2?
a) (2, -2)
b) (-2, 2)
c) (-2, -2)
d) (2, 2)
Question 26: Find the equation of median BE of the triangle ABC, with vertices A(1,2) , B(2,3) and C(3,6) ?
a) x=2
b) x=3
c) y=2
d) y=3
100+ Free GK Tests for SSC Exams
Question 27: What is the slope of the line perpendicular to the line 4x-3y=5 ?
a) -3/4
b) 4/3
c) 3/4
d) -4/3
Question 28: If P(2, 3) is the midpoint of A(4, y) and B(x, 1), then find y ?
a) 2
b) 3
c) 4
d) 5
Question 29: What is the reflection of the point ( 5, 2) in the line y = -1?
a) (-5, 4)
b) (-5, -4)
c) (5, -4)
d) (5, 4)
Question 30: Find the slope of the line joining A(-3, 2) and B(1, 4) ?
a) -1/2
b) 2
c) 1/2
d) -1
Question 31: What is the reflection of the point ( 1, 2) in the line x = -3?
a) (-7, -2)
b) (-7, 2)
c) (7, -2)
d) (7, 2)
Question 32: What is the reflection of the point ( 1, 2) in the line x = -3?
a) (-7, -2)
b) (-7, 2)
c) (7, -2)
d) (7, 2)
Question 33: Find the length of the median AD of a triangle ABC, with vertices A(1,2) , B(2,3) and C(0,5) ?
a) 1 unit
b) 2 units
c) 3 units
d) 4 units
Question 34: Find the slope of the line joining A(1,2) and B(1, -2) ?
a) -4
b) 0
c) 2
d) undefined
Question 35: Find the mid-point of the line joining A(3, -2) and B(-3, -2) ?
a) (3, -2)
b) (-3, 0)
c) (0, -2)
d) (0, 2)
Question 36: What is the reflection of the point ( -3, 2) in the line x = -2?
a) (-1, -2)
b) (-1, 2)
c) (1, -2)
d) (1, 2)
Question 37: Find the slope of the line joining A(-1, -5) and B(2, 4)
a) -3
b) 0
c) 3
d) -1
Question 38: Find the centroid of the triangle with vertices A(2,3), B(-3,2) & C(1,4) ?
a) (0,0)
b) (2,-3)
c) (0,3)
d) (3,0)
Question 39: What is the reflection of the point (4,2) about origin ?
a) (-4, -2)
b) (4, 2)
c) (-4, 2)
d) (4, -2)
Question 40: : Find the equation of the median AD of a triangle ABC, with vertices A(1,2) , B(2,3) and C(3,1) ?
a) y=1
b) y=2
c) y=3
d) y=4
Answers & Solutions:
1) Answer (D)
Orthocentre of a right angled triangle is the vertex where the angle is 90°
Here, it is right angled at A, so A(2, 3) is the orthocentre.
So the answer is option D.
2) Answer (B)
Eq.of a circle of radius r and having centre at ($x_1, y_1$) is $(x-x_1)^2+(y-y_1)^2=r^2$
Hence, $(x-1)^2+(y-2)^2=4^2$
==> $x^2-2x+1+y^2-4y+4 = 16$
==> $x^2+y^2-2x-4y-11 = 0$
So the answer is option B.
3) Answer (B)
(-4, 2) lies on left to the line x=-3
Distance between the line & point is -3-(-4) = 1
So its reflection must be 1 unit to the right side the line , i.e; (-3+1, 2) = (-2, 2)
So the answer is option B.
4) Answer (B)
Slope = $\frac{y_2-y_1}{x_2-x_1}$ = $\frac{2+1}{2-5} = 3/-3 = -1$
So the answer is option B.
5) Answer (C)
Let (x, y) be the coordinates of A, then
$(\frac{x-5}{2} , \frac{y-4}{2}) = (-1, -1)$
x-5 = -2 & y-4 = -2
x = 3 & y = 2
A = (x, y) = (3,2)
So the answer is option C.
6) Answer (B)
$P(x, y) = (\frac{mx_2+nx_1}{m+n}, \frac{my_2+ny_1}{m+n})$
$P(x, 3) = (\frac{-1m+3n}{m+n}, \frac{2m-n}{m+n})$
$\frac{2m-n}{m+n} = 3$
$2m-n = 3m+3n$
$-m = 4n$
$m/n = -4/1$
So the answer is option B.
7) Answer (D)
(-4, 3) lies 3 units left to the line x = -1
So its reflection must lie 3 unit right to the line,
So its reflection is (-1+3, 3) = (2, 3)
So the answer is option D.
8) Answer (A)
3x – 2y = 12 lines cuts Y-axis, where x = 0
3(0)-2y = 12
-2y = 12
y = -6
So the point is (0, -6)
So the answer is option A.
9) Answer (B)
Slope of a line ax+by+c = 0 is -a/b
Slope of line x-3y+2=0 = -1/-3 = 1/3
Slope of parallel line = 1/3
So the answer is option B.
10) Answer (D)
$P(x, y) = (\frac{mx_2+nx_1}{m+n}, \frac{my_2+ny_1}{m+n})$
$P(x, y) = (\frac{2(4)+3(2)}{2+3}, \frac{2(1)+3(3)}{2+3})$
$P(x, y) = (\frac{14}{5}, \frac{11}{5})$
So the answer is option D.
11) Answer (C)
Centroid $= (\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3})$
$(x, 2) = (\frac{2-1+2}{3}, \frac{y-3+6}{3})$
$(x, 2) = (1, \frac{y+3}{3})$
=> $x = 1$ , & $2 = (y+3)/3$
=> $x = 1$, & $y = 3$
$x*y = 3$
So the answer is option C.
12) Answer (A)
(-2, -2) lies 1 unit below the line y = -1
So its reflection must lie 1 unit above the line,
So its reflection is (-2, -1+1) = (-2, 0)
So the answer is option A.
13) Answer (B)
Put y = 0 in 3x + 2y = 12,
3x = 12
x = 4
So the point is (4,0)
So the answer is option B.
14) Answer (D)
slope of the line perpendicular to the line ax+by+c=0 is, b/a
slope of the line perpendicular to the line 2x+2y=3 is 2/2=1
So the answer is option D.
15) Answer (B)
Let the ratio be m:n
(3, Y) = ($\frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n}$)
3 = $\frac{4m+n}{m+n}$
3m+3n = 4m+n
2n = m
m/n = 2/1
So the answer is option B.
16) Answer (B)
Let A be (x, y)
(2,-1) = ($\frac{x+5}{2} , \frac{y-4}{2}$)
x+5 = 2*2 and y-4 = -1*2
x = 4-5 and y = -2+4
x = -1 and y = 2
A = (x,y) = (-1,2)
So the answer is option B.
17) Answer (C)

From the diagram answer is (-1,-1)
So the answer is option C.
18) Answer (C)
Slope = m = $\frac{y_2-y_1}{x_2-x_1}$ = $\frac{2-1}{-2+3}$ = $1$
Slope of perpendicular line = -1/m = -1/1 = -1
So the answer is option C.
19) Answer (A)
($\frac{2-1+x}{3} , \frac{3-3+y}{3}$) = (1, 2)
($\frac{1+x}{3} , \frac{y}{3}$) = (1, 2)
1+x = 3 and y = 6
x = 2 and y = 6
x-y = 2-6 = -4
So the answer is option A.
20) Answer (D)
Let the ratio is m:n
1 = $\frac{m(-1)+n(3)}{m+n}$
$m+n = -m+3n$
$2m = 2n$
$m:n = 1:1$
So the answer is option D.
21) Answer (C)
(4, 3) lies above the line y=-1
Distance b/w the line & point is 3-(-1) = 4
So its reflection must be 4 units below the line , i.e; (4, -1-4) = (4, -5)
So the answer is option C.
22) Answer (A)
E = mid point of AC = $(\frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2})$ = $(\frac{1+3}{2} , \frac{2+6}{2})$ = $(2, 4)$
B = (2 , 3) & E = ( 2 , 4)
Since x values are same,distance = $y_{2}-y_{1} = 4-3 = 1$
So the answer is option A.
23) Answer (A)
slope m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-2}{1+1}=-4/2=-2$
So the answer is option A.
24) Answer (C)
Mid point = $(\frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2})$
(2, 3) = $(\frac{4+x}{2} , \frac{1+y}{2})$
$\frac{4+x}{2}$ = 2
4+x = 4
x = 0
So the answer is option C.
25) Answer (A)
The point (2, -2) lies on the line y = -2, so reflection is itself
So the answer is option A.
26) Answer (A)
E = mid point of AC = $(\frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2})$ = $(\frac{1+3}{2} , \frac{2+6}{2})$ = $(2, 4)$
B = (2 , 3) & E = ( 2 , 4)
Since x values are same, Equation of BE is x = 2
So the answer is option A.
27) Answer (A)
Slope of a line ax+by+c = 0 is $\frac{-a}{b}$
Slope of the line 4x-3y=5 is m =-4/-3 = 4/3
Slope of a line perpendicular to this line = -1/m = -3/4
So the answer is option A.
28) Answer (D)
Mid point = $(\frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2})$
(2, 3) = $(\frac{4+x}{2} , \frac{1+y}{2})$
$\frac{1+y}{2}$ = 3
1+y = 6
y = 5
So the answer is option D.
29) Answer (C)
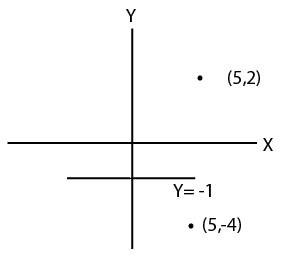
From the diagram reflection of (5 , 2) is (5 , -4)
So the answer is option C.
30) Answer (C)
slope m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{4-2}{1+3}=2/4=1/2$
So the answer is option C.
31) Answer (B)
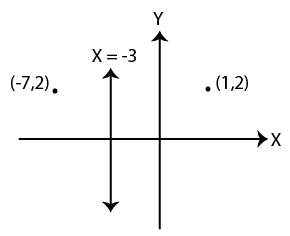
from the diagram answer is (-7 , 2)
So the answer is option B.
32) Answer (B)

from the diagram answer is (-7 , 2)
So the answer is option B.
33) Answer (B)
D = mid point of BC = $(\frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2})$ = $(\frac{2+0}{2} , \frac{3+5}{2})$ = $(1, 4)$
A = (1 , 2) & D = ( 1 , 4)
Since x values are same, Distance = $y_{2}-y_{1}=4-2=2$
So the answer is option B.
34) Answer (D)
slope m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-2}{1-1}=\infty$
So the answer is option D.
35) Answer (C)
Mid-point = $(\frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2})$ = $(\frac{3-3}{2} , \frac{-2-2}{2})$ = $( 0 , -2)$
So the answer is option C.
36) Answer (B)
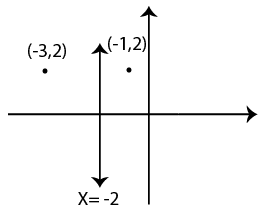
from the diagram answer is (-1 , 2)
So the answer is option B.
37) Answer (C)
slope m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{4+5}{2+1}=9/3=3$
So the answer is option C.
38) Answer (C)
Centroid = $(\frac{x_{1}+x_{2}+x_{3}}{3} , \frac{y_{1}+y_{2}+y_{3}}{3})$ = $(\frac{2-3+1}{3} , \frac{3+2+4}{3})$ = $(\frac{0}{3} , \frac{9}{3})$ = (0, 3)
So the answer is option C.
39) Answer (A)
To find reflection about origin, just change the signs.
reflection of the point (4,2) about origin is (-4, -2)
So the answer is option A.
40) Answer (B)
A(1,2) , B(2,3) and C(3,1)
D = mid point of B and C = $(\frac{2+3}{2} , \frac{3+1}{2})$ = $(\frac{5}{2} , \frac{4}{2})$ = $(5/2 , 2)$
A(1 , 2) , D(5/2 , 2)
Equation of AD is y = 2 ($\because$ y value is same for both points)
So the answer is option B.
Download SSC GD Previous Papers PDF
DOWNLOAD APP FOR SSC FREE MOCKS
We hope this Coordinate Geometry questions for SSC GD will be highly useful for your preparation.





