Geometry Circles Questions for CAT

Geometry Circles questions are important concepts in the Geometry concept of the CAT Quant section. These questions are not very tough; make sure you are aware of all the Important Formulas in CAT Geometry. Solve more questions from CAT Geometry Circles. You can check out these CAT Geometry questions from the CAT Previous year papers. Practice a good number of questions in CAT Geometry Circles so that you can answer these questions with ease in the exam. In this post, we will look into some important CAT Geometry Questions. These are a good source of practice for CAT 2022 preparation; If you want to practice these questions, you can download these Important Circles (Geometry) Questions for CAT (with detailed answers) PDF along with the video solutions below, which is completely Free.

Download Geometry Circles Questions for CAT

Enroll for CAT 2022 Crash Course

Question 1: In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?

a) 17.05

b) 27.85

c) 22.45

d) 32.25

e) 26.25

1) Answer (E)

View Video Solution

Solution:

Let x be the value of third side of the triangle. Now we know that Area = 17.5*9*x/(4*R), where R is circumradius.

Also Area = 0.5*x*3 .

Equating both, we have 3 = 17.5*9 / (2*R)

=> R = 26.25.

Question 2: Two circles, both of radii 1 cm, intersect such that the circumference of each one passes through the centre of the other. What is the area (in sq. cm.) of the intersecting region?

a) $\frac{\pi}{3}-\frac{\sqrt 3}{4}$

b) $\frac{2\pi}{3}+\frac{\sqrt 3}{2}$

c) $\frac{4\pi}{3}-\frac{\sqrt 3}{2}$

d) $\frac{4\pi}{3}+\frac{\sqrt 3}{2}$

e) $\frac{2\pi}{3}-\frac{\sqrt 3}{2}$

2) Answer (E)

View Video Solution

Solution:

The circumferences of the two circle pass through each other’s centers. Hence, O1A = O1B=O1O2 = 1cm

By symmetry, the line joining the two centres would be bisect AB and would be bisected by AB. As the line joining the center to the midpoint of a chord is perpendicular to the chord, O1O2 and AB are perpendicular bisectors of each other. Suppose they intersect at point P.

O1P = Half of O1O2 = 1/2 cm
So, the angle AO1P = 60 degrees as cos 60 = 1/2
By symmetry, BO1P = 60 degrees.
So, angle AO1B= 120 degrees

In the above, the required area is 2 times A(segment ABO2)(blue region). And A(segment ABO2)(blue region) = A(sector O2AO1B)(blue + red) – A(triangleO1AB )(red)

Area of sector = 120°/360° * $\pi * 1^2 $ = $\pi/3$

Area of triangle = 1/2 * b * h = 1/2 * (2* 1 cos 30°) * (1/2) = √3/4

Hence, required area = $\frac{\pi}{3}-\frac{\sqrt 3}{4}$ . Hence so the required area is 2 times the above value which is $\frac{2\pi}{3}-\frac{\sqrt 3}{2}$

Question 3: In the figure below, AB is the chord of a circle with center O. AB is extended to C such that BC = OB. The straight line CO is produced to meet the circle at D. If $\angle{ACD}$ = y degrees and $\angle{AOD}$ = x degrees such that x = ky, then the value of k is

a) 3

b) 2

c) 1

d) None of the above.

3) Answer (A)

View Video Solution

Solution:

Since Angle BOC = Angle BCO = y.

Angle OBC = 180-2y .

Hence Angle ABO =  z = 2y = Angle OAB.

Now since x is exterior angle of triangle AOC .

We have x = z + y = 3y.

Hence option A.

Question 4: What is the distance in cm between two parallel chords of lengths 32 cm and 24 cm in a circle of radius 20 cm?

a) 1 or 7

b) 2 or 14

c) 3 or 21

d) 4 or 28

4) Answer (D)

View Video Solution

Solution:

The distances of the chords from the center are 12 cm and 16 cm respectively.

If the chords lie on the same side of the center, the distance between the chords is 4 cm, if they lie on opposite sides of the center, the distance between them is 28 cm.

Question 5: Two identical circles intersect so that their centres, and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is

a) $\pi$/4

b) $\pi$/2-1

c) $\pi$/5

d) $\sqrt\pi-1$

5) Answer (B)

View Video Solution

Solution:

We know that quad ambn is a square of side 1.

Area of the sector a-mqn is $\frac{90}{360}* \pi *1*1$ = $\frac{\pi }{4}$.

Area of square = 1*1 = 1

Area of common portion = 2 * Area of sector – Area of square

= 2 * $\frac{\pi }{4}$ – 1 =  $\frac{\pi }{2}$ – 1

Question 6: In the following figure, the diameter of the circle is 3 cm. AB and MN are two diameters such that MN is perpendicular to AB. In addition, CG is perpendicular to AB such that AE:EB = 1:2, and DF is perpendicular to MN such that NL:LM = 1:2. The length of DH in cm is

a) $2\sqrt2 – 1$

b) $(2\sqrt2 – 1)/2$

c) $(3\sqrt2 – 1)/2$

d) $(2\sqrt2 – 1)/3$

6) Answer (B)

View Video Solution

Solution:

Let EO = x, So, AE = 1.5 – x
AE : EB = 1:2 => x = 1/2

(1.5-x):(1.5+x) = 1:2.

x=0.5.

So, EO = 0.5
Similarly, OL = 0.5
Now, EOLH is a parallelogram and EO = OL = 0.5
In triangle DOL, DO = radius = 1.5 and OL = 0.5
So, DL = $\sqrt2$
=> DH = $(2\sqrt2 – 1)/2$

Checkout: CAT Free Practice Questions and Videos

Question 7: Consider a circle with unit radius. There are 7 adjacent sectors, S1, S2, S3,….., S7 in the circle such that their total area is (1/8)th of the area of the circle. Further, the area of the $j^{th}$ sector is twice that of the $(j-1)^{th}$ sector, for j=2, …… 7. What is the angle, in radians, subtended by the arc of S1 at the centre of the circle?

a) $\pi/508$

b) $\pi/2040$

c) $\pi/1016$

d) $\pi/1524$

7) Answer (A)

View Video Solution

Solution:

Now area of 1st sector = $\pi * r^2 * \frac{x}{360}$ where x – angle subtended at center

Now the next sector will have 2x as the angle, and similarly angles will be in GP with ratio = 2.

Sum of areas of all 7 sectors = $\frac{127*x* \pi * r^2}{360}$ which is equal to $\frac{\pi * r^2}{8}$

We get x = $\frac{360}{8*127}$

Now if converted in radians we get  x = $\pi/508$.

Question 8: In the following figure, ACB is a right-angled triangle. AD is the altitude. Circles are inscribed within the triangle ACD and triangle BCD. P and Q are the centers of the circles. The distance PQ is

The length of AB is 15 m and AC is 20 m

a) 7 m

b) 4.5 m

c) 10.5 m

d) 6 m

8) Answer (A)

View Video Solution

Solution:

By Pythagoras theorem we get BC = 25 . Let BD = x;Triangle ABD is similar to triangle CBA => AD/15 = x/20 and also triangle ADC is similar to triangle ACB=> AD/20 = (25-x)/15. From the 2 equations, we get x = 9 and DC = 16

We know that AREA = (semi perimeter ) * inradius

For triangle ABD, Area = 1/2 x BD X AD = 1/2 x 12 x 9 = 54 and semi perimeter = (15 + 9 + 12)/2 = 18. On using the above equation we get, inradius, r = 3.

Similarly for triangle ADC we get inradius R = 4 .

PQ = R + r = 7 cm

Question 9: A circle is inscribed in a given square and another circle is circumscribed about the square. What is the ratio of the area of the inscribed circle to that of the circumscribed circle?

a) 2 : 3

b) 3 : 4

c) 1 : 4

d) 1 : 2

9) Answer (D)

View Video Solution

Solution:

As we know that area of the circle is directly proportional to the square of its radius.
Hence $\frac{A_{ic}}{A_{cc}} = \frac{\frac{x^2}{4}}{\frac{x^2}{2}}$
Where $x$ is side of square (say), ic is inscribed circle with radius $\frac{x}{2}$, cc is circumscribed circle with radius $\frac{x}{\sqrt{2}}$
So ratio will be 1:2

Question 10: The figure shows the rectangle ABCD with a semicircle and a circle inscribed inside in it as shown. What is the ratio of the area of the circle to that of the semicircle?

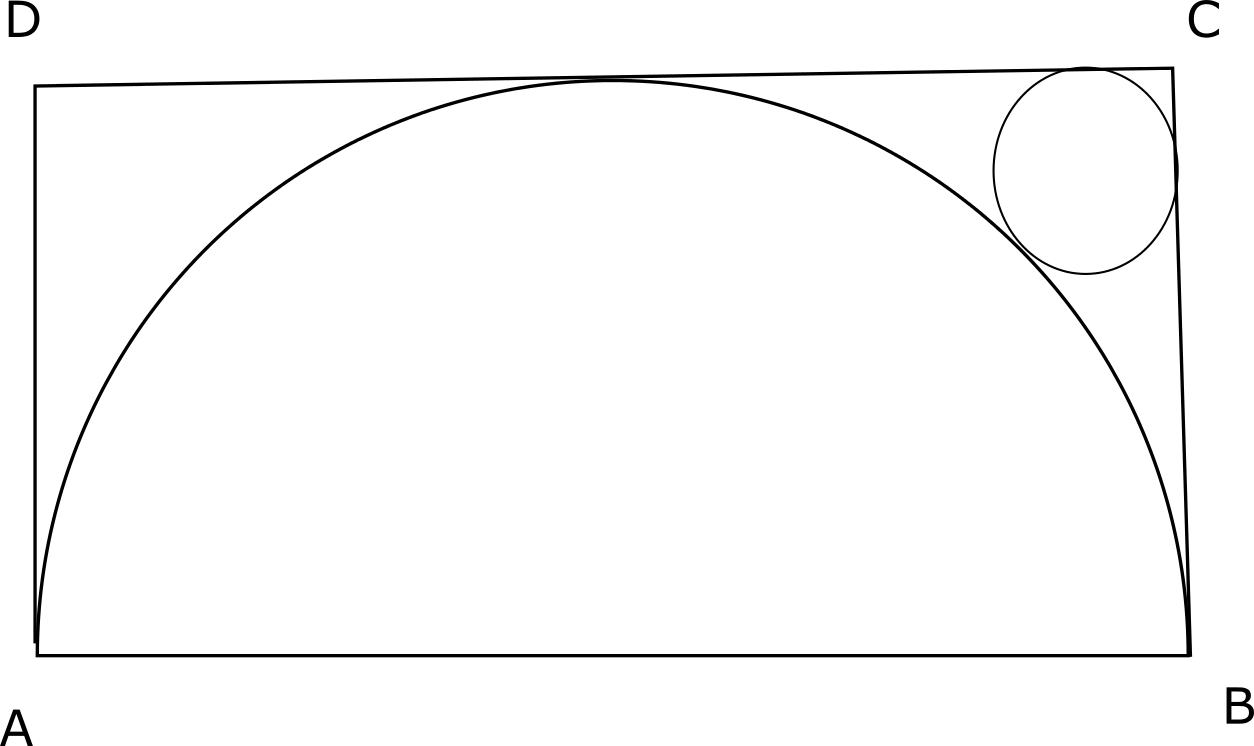
a) $(\sqrt2 -1)^{2}:1$

b) $2(\sqrt{2} -1)^2 :1$

c) $(\sqrt2-1)^2 :2$

d) None of these

10) Answer (D)

View Video Solution

Solution:

Let the center be O and the point at which the semicircle intersects CD be P.

Let the radius of the semicircle be R and the circle be r.

OP = R and OC = R$\sqrt{2}$

OC – OT = CC’ – TC’

$R\sqrt{2} – R – 2r$ = $r\sqrt{2} – r$

=> $R\sqrt{2} – R$ = $r\sqrt{2} + r$

=> r = $\frac{(\sqrt{2}-1)R}{\sqrt{2}+1}$

=> r = $(\sqrt{2}-1)^2$R

Ratio of areas will be $r^2 : \frac{R^2}{2}$ = $2(\sqrt{2}-1)^4$ : 1

Important Geometry Videos | Quant Preparation Videos

Check out the CAT Formula Handbook which includes the most important formulas you must know for CAT.