XAT Geometry Questions [Download PDF]
Download Geometry Questions for XAT PDF. Practice XAT solved Geometry Questions paper tests, and these are the practice question to have a firm grasp on the Geometry topic in the XAT exam. Top 10 very Important Geometry Questions for XAT based on asked questions in previous exam papers. The XAT question papers contain actual questions asked with answers and solutions.
Download Geometry Questions for XAT
Enroll to XAT 2024 Crash Course
Question 1:
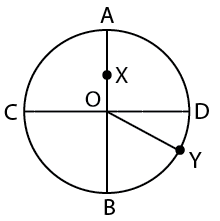
In a circular field, AOB and COD are two mutually perpendicular diameters having length of 4 meters. X is the mid – point of OA. Y is the point on the circumference such that ∠YOD = 30°. Which of the following correctly gives the relation among the three alternate paths from X to Y?
a) XOBY : XODY : XADY :: 5.15 : 4.50 : 5.06
b) XADY : XODY : XOBY :: 6.25 : 5.34 : 4.24
c) XODY : XOBY : XADY :: 4.04 : 5.35 : 5.25
d) XADY : XOBY : XODY :: 5.19 : 5.09 : 4.04
e) XOBY : XADY : XODY :: 5.06 : 5.15 : 4.50
1) Answer (D)
Solution:
XADY = XA + AD + DY = 2/2 + (2 * 3.14 * 2)/4 + (30/360) * (2 * 3.14 * 2) = 5.19
XOBY = XO + OB + BY = 2/2 + 2 + (60/360) * (2 * 3.14 * 2) = 5.09
XODY = XO + OD + DY = 2/2 + 2 + (30/360) * (2 * 3.14 * 2) = 4.04
Hence, option D is the correct answer.
Question 2: Let $S_{1}, S_{2},…$ be the squares such that for each n ≥ 1, the length of the diagonal of $S_{n}$ is equal to the length of the side of $S_{n+1}$. If the length of the side of $S_{3}$ is 4 cm, what is the length of the side of $S_{n}$ ?
a) $2^[{\frac{2n+1}{2}}]$
b) $2.(n-1)$
c) $2^{n-1}$
d) $2^[{\frac{n+1}{2}}]$
e) None of these
2) Answer (D)
Solution:
Length of side of $S_{n + 1}$ = Length of diagonal of $S_n$
=> Length of side of $S_{n + 1}$ = $\sqrt{2}$ (Length of side of $S_{n}$)
=> $\frac{\textrm{Length of side of }S_{n + 1}}{\textrm{Length of side of }S_n} = \sqrt{2}$
=> Sides of $S_1 , S_2 , S_3 , S_4,…….., S_n$ form a G.P. with common ratio, $r = \sqrt{2}$
It is given that, $S_3 = ar^2 = 4$
=> $a (\sqrt{2})^2 = 4$
=> $a = \frac{4}{2} = 2$
$\therefore$ $n^{th}$ term of G.P. = $a (r^{n – 1})$
= $2 (\sqrt{2})^{n – 1}$
=$2^[{\frac{n+1}{2}}]$
Question 3: In the figure below, AB = AC = CD. If ADB = 20°, what is the value of BAD?

a) 40°
b) 60°
c) 70°
d) 120°
e) 140°
3) Answer (D)
Solution:
AB = AC = CD, => $\angle CAD = \angle CDA = 20^{\circ}$
and $\angle ABC = \angle ACB$
In $\triangle$ ACD
=> $\angle ACD + \angle CAD + \angle CDA = 180^{\circ}$
=> $\angle ACD = 180^{\circ} – 20^{\circ} – 20^{\circ} = 140^{\circ}$
=> $\angle ACB = 180^{\circ} – 140^{\circ} = 40^{\circ} = \angle ABC$
Similarly, In $\triangle$ ABC
=> $\angle BAC = 180^{\circ} – 40^{\circ} – 40^{\circ} = 100^{\circ}$
$\therefore \angle BAD = 100^{\circ} + 20^{\circ} = 120^{\circ}$
Question 4: The difference between the area of the circumscribed circle and the area of the inscribed circle of an equilateral triangle is 2156 sq. cm. What is the area of the equilateral triangle?
a) 686√3
b) 1000
c) 961√2
d) 650√3
e) None of the above
4) Answer (A)
Solution:
Let radius of incircle = $r$, => Radius of circumcircle = $2r$
Difference in area = $\pi [(2r)^2 – (r)^2] = 2156$
=> $3 \times \frac{22}{7} \times r^2 = 2156$
=> $r^2 = \frac{2156 \times 7}{66}$
=> $r = \sqrt{\frac{686}{3}}$
Now, height of equilateral triangle = $3 r = \frac{\sqrt{3}}{2} a$ (where $a$ is side of triangle)
=> $3 \times \sqrt{\frac{686}{3}} = \frac{\sqrt{3}}{2} a$
=> $a = 2 \sqrt{686}$
$\therefore$ Area of triangle = $\frac{\sqrt{3}}{4} a^2$
= $\frac{\sqrt{3}}{4} \times 4 \times 686 = 686 \sqrt{3} cm^2$
Question 5: A solid metal cylinder of 10 cm height and 14 cm diameter is melted and re – cast into two cones in the proportion of 3 : 4 (volume), keeping the height 10 cm. What would be the percentage change in the flat surface area before and after?
a) 9%
b) 16%
c) 25%
d) 50%
e) None of the above
5) Answer (D)
Solution:
Volume of Cylinder = $\pi r^2 h = \pi \times 7^2 \times 10 = 490\pi$
Now, The solid metal cylinder is re-cast into two cones in the proportion 3 : 4 i.e. the volumes of cone 1 and cone 2 is
$210 \pi$ and $280 \pi$ respectively.
So, flat Surface area of cylinder before melting = $2 \pi r^2 = 2 \pi \times 7^2 = 98 \pi$
Volume of cone 1 = $\frac{1}{3} \pi r_1^2 h = 210 \pi$
=> $r_1^2 = \frac{210 \times 3}{10} = 63$
Volume of cone 2 = $\frac{1}{3} \pi r_2^2 h = 280 \pi$
=> $r_2^2 = \frac{280 \times 3}{10} = 84$
Flat surface area of cones = $\pi r_1^2 + \pi r_2^2$
= $\pi (63 + 84) = 147 \pi$
$\therefore$ Percentage change in surface area = $\frac{147 \pi – 98 \pi}{98 \pi} \times 100$
= $\frac{1}{2} \times 100 = 50 \%$
Question 6: Two diagonals of a parallelogram intersect each other at coordinates (17.5, 23.5). Two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16). Find the lengths of the diagonals.
a) 15 and 30
b) 15 and 40
c) 17 and 30
d) 17 and 40
e) Multiple solutions are possible
6) Answer (D)
Solution:

Using distance formula,
$CX = \sqrt{(17.5 – 5.5)^2 + (23.5 – 7.5)^2} = \sqrt{12^2 + 16^2}$
= $\sqrt{144 + 256} = \sqrt{400} = 20$
=> $AC = 2 \times CX = 40$
$BX = \sqrt{(17.5 – 13.5)^2 + (23.5 – 16)^2} = \sqrt{4^2 + 7.5^2}$
= $\sqrt{16 + 56.25} = \sqrt{72.25} = 8.5$
=> $BD = 2 \times BX = 17$
Question 7: In quadrilateral PQRS, PQ = 5 units, QR = 17 units, RS = 5 units, and PS = 9 units. The length of the diagonal QS can be:
a) > 10 and < 12
b) > 12 and < 14
c) > 14 and < 16
d) > 16 and < 18
e) cannot be determined
7) Answer (B)
Geometry
Solution:
In a triangle , sum of two sides is greater than the third side and difference of two sides is less than third side.
In $\triangle$ PQS
=> $QS < 9 + 5$ => $QS < 14$ ——Eqn(I)
In $\triangle$ QRS
=> $QS > 17 – 5$ => $QS > 12$ ——Eqn(II)
From eqn(I) & (II)
=> $12 < QS < 14$
Question 8: There are two circles $C_{1}$ and $C_{2}$ of radii 3 and 8 units respectively. The common internal tangent, T, touches the circles at points $P_{1}$ and $P_{2}$ respectively. The line joining the centers of the circles intersects T at X. The distance of X from the center of the smaller circle is 5 units. What is the length of the line segment $P_{1} P_{2}$ ?
a) ≤ 13
b) > 13 and ≤ 14
c) > 14 and ≤ 15
d) > 15 and ≤ 16
e) > 16
8) Answer (C)
Solution:

Given : $OP_1 = 3 , O’P_2 = 8 , OX = 5$ units
To find : $P_1P_2 = ?$
Solution : In $\triangle OP_1X$
=> $(P_1X)^2 = (OP_1)^2 – (OX)^2$
=> $(P_1X)^2 = 5^2 – 3^2 = 25 – 9$
=> $P_1X = \sqrt{16} = 4$
In $\triangle OP_1X$ and $\triangle O’P_2X$
$\angle OXP_1 = O’XP_2$ (Vertically opposite angles)
$\angle OP_1X = O’P_2X = 90$
=> $\triangle OP_1X \sim \triangle O’P_2X$
=> $\frac{XP_1}{XP_2} = \frac{OP_1}{O’P_2}$
=> $XP_2 = 4 \times \frac{8}{3} = 10.66$
$\therefore P_1P_2 = P_1X + XP_2 = 4 + 10.66 = 14.66$ units
Question 9: There are two squares S 1 and S 2 with areas 8 and 9 units, respectively. S 1 is inscribed within S 2 , with one corner of S 1 on each side of S 2 . The corners of the smaller square divides the sides of
the bigger square into two segments, one of length ‘a’ and the other of length ‘b’, where, b > a. A possible value of ‘b/a’, is:
a) ≥ 5 and < 8
b) ≥ 8 and < 11
c) ≥ 11 and < 14
d) ≥ 14 and < 17
e) > 17
9) Answer (D)
Solution:

Area of $S_1 = 8$ sq. units
=> Side of $S_1 = PS = \sqrt{8} = 2 \sqrt{2}$ units
Similarly, Side of $S_2 = CD = \sqrt{9} = 3$ units
=> $a + b = 3$
In $\triangle$ PDS
=> $b^2 + a^2 = 8$
=> $b^2 + (3 – b)^2 = 8$
=> $b^2 + 9 + b^2 – 6b = 8$
=> $2b^2 – 6b + 1 = 0$
=> $b = \frac{6 \pm \sqrt{36 – 8}}{4} = \frac{6 \pm \sqrt{28}}{4}$
=> $b = \frac{3 + \sqrt{7}}{2}$ $(\because b > a)$
=> $a = 3 – \frac{3 + \sqrt{7}}{2} = \frac{3 – \sqrt{7}}{2}$
$\therefore \frac{b}{a} = \frac{\frac{3 + \sqrt{7}}{2}}{\frac{3 – \sqrt{7}}{2}}$
= $\frac{3 + \sqrt{7}}{3 – \sqrt{7}} \approx 15.9$
Question 10: A spherical metal of radius 10 cm is molten and made into 1000 smaller spheres of equal sizes. In this process the surface area of the metal is increased by:
a) 1000 times
b) 100 times
c) 10 times
d) No change
e) None of the above
10) Answer (E)
Solution:
Radius of larger sphere = $R = 10$ cm
Let radius of each of the smaller spheres = $r$ cm
=> $\frac{4}{3} \pi R^3 = 1000 \times \frac{4}{3} \pi r^3$
=> $10^3 = 1000 r^3$
=> $r = \sqrt[3]{1} = 1$ cm
Initial surface area of sphere = $4 \pi R^2 = 4 \pi \times 100 = 400 \pi$
Final surface area of 1000 spheres = $1000 \times 4 \pi r^2 = 1000 \times 4 \pi = 4000 \pi$
$\therefore$ Increase in surface area = $4000 \pi – 400 \pi = 3600 \pi$
=> $\frac{3600 \pi}{400 \pi} = 9$ times







