Venn Diagram Questions for IIFT
Download important IIFT Venn Diagram Questions PDF based on previously asked questions in IIFT and other MBA exams. Practice Venn Diagram Questions and answers for IIFT and other exams.
Download Venn Diagram Questions for IIFT
Get 5 IIFT mock tests for Rs. 299. Enroll here
Download IIFT Previous Papers PDF
Take IIFT Mock Tests (With Solutions)
Question 1: A survey was conducted of 100 people to find out whether they had read recent issues of Golmal, a monthly magazine. The summarized information regarding readership in 3 months is given below:Only September: 18;September but not August: 23;September and July: 8;September:28;July: 48;July and August: 10;none of the three months: 24What is the number of surveyed people who have read exactly two consecutive issues (out of the three)?
a) 7
b) 9
c) 12
d) 14
e) 17
Instructions
Help Distress (HD) is an NGO involved in providing assistance to people suffering from natural disasters. Currently, it has 37 volunteers. They are involved in three projects: Tsunami Relief (TR) in Tamil Nadu, Flood Relief (FR) in Maharashtra, and Earthquake Relief (ER) in Gujarat. Each volunteer working with Help Distress has to be involved in at least one relief work project.
- A Maximum number of volunteers are involved in the FR project. Among them, the number of volunteers involved in FR project alone is equal to the volunteers having additional involvement in the ER project.
- The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects.
- 17 volunteers are involved in the TR project.
- The number of volunteers involved in the TR project alone is one less than the number ofvolunteers involved in ER project alone.
- Ten volunteers involved in the TR project are also involved in at least one more project.
Question 2: Based on the information given above, the minimum number of volunteers involved in both FR and TR projects, but not in the ER project is:
a) 1
b) 3
c) 4
d) 5
Question 3: Which of the following additional information would enable to find the exact number of volunteers involved in various projects?
a) Twenty volunteers are involved in FR.
b) Four volunteers are involved in all the three projects.
c) Twenty three volunteers are involved in exactly one project.
d) No need for any additional information.
Question 4: After some time, the volunteers who were involved in all the three projects were asked to withdraw from one project. As a result, one of the volunteers opted out of the TR project, and one opted out of the ER project, while the remaining ones involved in all the three projects opted out of the FR project. Which of the following statements, then, necessarily follows?
a) The lowest number of volunteers is now in TR project.
b) More volunteers are now in FR project as compared to ER project.
c) More volunteers are now in TR project as compared to ER project.
d) None of the above.
Question 5: After the withdrawal of volunteers, as indicated in the previous question, some new volunteers joined the NGO. Each one of them was allotted only one project in a manner such that, the number of volunteers working in one project alone for each of the three projects became identical. At that point, it was also found that the number of volunteers involved in FR and ER projects was the same as the number of volunteers involved in TR and ER projects. Which of the projects now has the highest number of volunteers?
a) ER
b) FR
c) TR
d) Cannot be determined
Question 6: Shyam visited Ram during his brief vacation. In the mornings they both would go for yoga. In the evenings they would play tennis. To have more fun, they indulge only in one activity per day, i.e. either they went for yoga or played tennis each day. There were days when they were lazy and stayed home all day long. There were 24 mornings when they did nothing, 14 evenings when they stayed at home, and a total of 22 days when they did yoga or played tennis. For how many days Shyam stayed with Ram?
a) 32
b) 24
c) 30
d) None of these
Question 7: In a locality, two-thirds of the people have cable TV, one-fifth have VCR, and one-tenth have both. What is the fraction of people having atleast one among cable -TV and VCR?
a) $\frac{19}{30}$
b) $\frac{2}{3}$
c) $\frac{17}{30}$
d) $\frac{23}{30}$
Question 8: There are 240 second year students in a B – School. The Finance area offers 3 electives in the second year. These are Financial Derivatives, Behavioural Finance, and Security Analysis. Four students have taken all the three electives, and 48 students have taken Financial Derivatives. There are twice as many students who study Financial Derivatives and Security Analysis but not Behavioural Finance, as those who study both Financial Derivatives and Behavioural Finance but not Security Analysis, and 4 times as many who study all the three. 124 students study Security Analysis. There are 59 students who could not muster courage to take up any of these subjects. The group of students who study both Financial Derivatives and Security Analysis but not Behavioural Finance, is exactly the same as the group made up of students who study both Behavioural Finance and Security Analysis. How many students study Behavioural Finance only?
a) 29
b) 30
c) 32
d) 35
e) None of the above
Question 9: 290 students of MBA (International Business) in a reputed Business School have to study foreign language in Trimesters IV and V. Suppose the following information are given .
i. 120 students study Spanish
ii. 100 students study Mandarin
iii. At least 80 students, who study a foreign language, study neither Spanish nor Mandarin
Then the number of students who study Spanish but not Mandarin could be any number from
a) 80 to 170
b) 80 to 100
c) 50 to 80
d) 20 to 110
Question 10: Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
Get Complete MBA Test Series for Rs. 799
Answers & Solutions:
1) Answer (B)

Let the areas be labelled as shown in the diagram above.
The number of people corresponding to “none of the three months” is 24. So, H is 24.
Only September is 18. So, G = 18
September but not August is 23. So, G + D = 23.
Hence, D = 23 – 18 = 5.
We know that September and July is 8. So, D + E = 8
This implies E = 3.
September = 28. So, D + E + F + G = 28.
So, F = 28 – 5 – 3 – 18 = 2.
July and August = 10.
So, B + E = 10.
E = 3. So, B = 7.
July = 48.
So, A + B + D + E = 48
A = 48 – 7 – 5 – 3 = 33.
There are 100 people in total. So, C = 100 – A – B – D – E – F – G – H = 100 – 33 – 7 – 5 – 3 – 2 – 18 – 24 = 8
So, number of people who read exactly two consecutive issues = (July & August) + (August & September) = B + F = 7 + 2 = 9
2) Answer (C)
Total number of volunteers are 37
=> 2x+y+x+y+x+y+z+10-z-x+2x-1=37
=> 5x+2y+9=37
=> 5x+2y=28
Also we know that 3x + 2y = 20.
We get x=4, => y=4
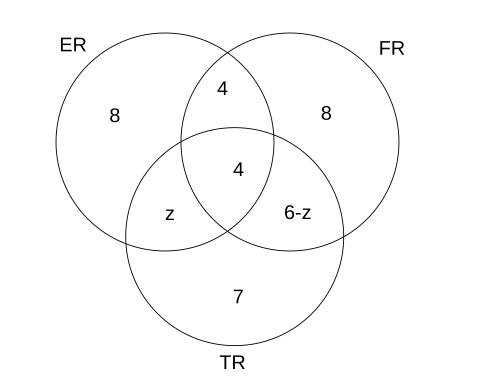
We need to find the minimum value of 6-z, and it is given FR get the most number of volunteers, We get that z cannot be more than 2 because if it is 3 or above ER will have the maximum number of volunteers.
3) Answer (A)
We can get the information mentioned in options B and C using the data given in the passage.
But, we need the information in option A to find the exact number of volunteers in various projects.
Hence, option A is the answer.
4) Answer (B)
So we can see that even if volunteers are withdrawn , the number of volunteers in FR are more as in, total if we calculate comes out to be more. Hence option B.
5) Answer (A)
Consider p volunteers be added to TR project and q be added to each of FR and ER projects.
Then, 7 + p = 8 + q => p = q + 1
Also, Number of volunteers working on TR = 7 + q + 1 + 4 + 5 = 17 + q
Number of volunteers working on FR = 17 + q
Number of volunteers working on ER = 18 + q.
So if we take any values we get ER greater than both FR and TR.
Take IIFT Mock Tests (With Solutions)
6) Answer (C)
Let the number of lazy days=x
They played tennis for 24-x days
They did yoga for 14-x days
So, they did yoga or played tennis for 24-x+14-x = 38-2x days
38-2x=22
x = 8
Number of lazy days=8
Number of days where they played yoga or tennis = 22
Number of Shyam stayed with Ram = 22+8=30
7) Answer (D)

Let the distribution of people having cable TV and VCR be as given in the diagram above.
Hence, $a+c =\frac{2}{3}$
$b+c=\frac{1}{5}$
and $c=\frac{1}{10}$
We need to find $a+b+c=?$
This equals $(a+b)+(b+c)-c = \frac{2}{3}+\frac{1}{5}-\frac{1}{10}$
Which equals $\frac{20+6-3}{30}=\frac{23}{30}$
8) Answer (A)

Given : $e = 4$
$FD = 48$, => $a + b + d + e = 48$
$d = 2b$ and $d = 4e$
$SA = 124$, => $d + e + f + g = 124$
$d = e + f$ and $h = 59$
To find : $c = ?$
Solution : $d = 4e = 4 \times 4 = 16$
=> $b = \frac{d}{2} = \frac{16}{2} = 8$
=> $f = d – e = 16 – 4 = 12$
=> $a = 48 – b – d – e = 48 – 8 – 16 – 4 = 20$
=> $g = 124 – d – e – f = 124 – 16 – 4 – 12 = 92$
Now, we know that, $a + b + c + d + e + f + g + h = 240$
=> $20 + 8 + c + 16 + 4 + 12 + 92 + 59 = 240$
=> $c + 211 = 240$
=> $c = 240 – 211 = 29$
9) Answer (D)

It’s given that 120 students study Spanish : A + B = 120 …(1)
Also 100 students study Mandarin : B + C = 100 …(2)
At least 80 students will not opt for any of these two languages i.e.
Spanish + Mandarin $\leq$ (290-80)
Spanish + Mandarin $\leq$ 210
A + B + C $\leq$ 210
Case 2: When B is minimum and A is maximum.
Solving for boundary condition A + B + C = 210 …(3)
Solving equations (1)+(2)-(3)
B = 10
i.e. A = 120 – B = 120 – 10 =110 {Maximum possible value of A}
Case 2: When B is maximum and A is minimum.
Since B+C = 100 so, Maximum value B can attain is 100. Hence, the minimum value of A = 120 – B = 120 – 100 = 20 {Minimum possible value of A}
So we can say that the number of students who study Spanish but not Mandarin will be A [20 ,110].
10) Answer: 52
Let us draw a Venn diagram using the information present in the question.
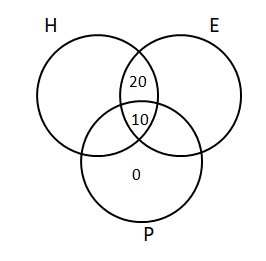
It is given that the number of students studying H equals that studying E.
Let ‘x’ be the total number of students who studied H, and H and P but mot E.We can also say that the same will be the number of students who studied E, and E and P but not H.Therefore,
x + 20 + 10 + x = 74
x = 22
Hence, the number of students studying H = 22 + 10+ 20 = 52
IIFT Previous year question papers PDF
We hope this Venn Diagram questions and answers for IIFT PDF will be helpful to you.







![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)