Mensuration Questions for SSC CGL Set-3 PDF
Download SSC CGL Mensuration questions with answers PDF based on previous papers very useful for SSC CGL exams. Very important Geometry questions for SSC exams.
Download Mensuaration Questions for SSC CGL Set-3 PDF
Get 790+ mocks for Rs. 100 – Coupon GOVTJOB
Question 1: The circumference of a circle is 88 cm. Find its radius (in cm).
a) 28
b) 15
c) 14
d) 30
Question 2: The volume of a hemisphere is 19404 cm3. Find its diameter (in cm).
a) 42
b) 21
c) 84
d) 63
Question 3: If the perimeter of a semicircle is 36 cm, then find its area (in $cm^{2}$)
a) 154
b) 35
c) 77
d) 70
Question 4: The lengths of the two diagonals of a rhombus are 7 cm and 24 cm. Find the length of its perimeter (in cm).
a) 25
b) 100
c) 75
d) 50
Question 5: Find the total surface area (in $cm^{2}$) of a right circular cone of diameter 21 cm and slant height 11 cm.
a) 467.5
b) 384
c) 724
d) 709.5
SSC CGL Previous Papers Download PDF
Question 6: Calculate the area (in $cm^{2}$) of a circle of radius 17.5 cm.
a) 1925
b) 962.5
c) 809.5
d) 1619
Question 7: The area of an equilateral triangle is 25√3 $cm^{2}$. Find its side (in cm).
a) 10
b) 5
c) 20
d) 30
Question 8: Find the total surface area $(in cm^2)$ of a cuboid of length, breadth and height of 10.5 cm, 8 cm and 9 cm respectively.
a) 607
b) 767
c) 769
d) 501
Question 9: The length of the diagonal and the breadth of a rectangle is 26 cm and 10 cm respectively. Calculate its area $(in cm^2)$
a) 480
b) 96
c) 240
d) 192
Question 10: Find the total surface area (in cm²) of a right circular cylinder of diameter 42 cm and height 14 cm.
a) 4488
b) 4250
c) 4010
d) 4620
18000+ Questions – Free SSC Study Material
Answers & Solutions:
1) Answer (C)
Let radius of circle = $r$ cm
=> Circumference = $2\pi r=88$
=> $2\times\frac{22}{7}\times r=88$
=> $r=88\times\frac{7}{44}$
=> $r=2\times7=14$ cm
=> Ans – (C)
2) Answer (A)
Let radius of hemisphere = $r$ cm
Volume of hemisphere = $\frac{2}{3}\times\pi r^3$
=> $\frac{2}{3}\times\frac{22}{7}\times(r)^3=19404$
=> $(r)^3=19404\times\frac{21}{44}$
=> $(r)^3=441\times21$
=> $r=\sqrt[3]{21\times21\times21}=21$ cm
$\therefore$ Diameter = $2\times21=42$ cm
=> Ans – (A)
3) Answer (C)
Let radius of semi circle = $r$ cm
=> Perimeter of semi circle = $\pi r+2r=36$
=> $r(\frac{22}{7}+2)=36$
=> $r(\frac{22+14}{7})=36$
=> $r=36\times\frac{7}{36}=7$ cm
$\therefore$ Area of semi-circle = $\frac{1}{2} \pi r^2$
= $\frac{1}{2}\times\frac{22}{7}\times(7)^2$
= $11\times7=77$ $cm^2$
=> Ans – (C)
4) Answer (D)
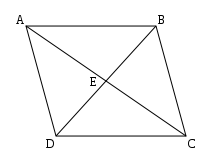
Given : ABCD is a rhombus and AC = 24 cm and BD = 7 cm
To find : Perimeter of ABCD
Solution : Diagonals of a rhombus bisect each other at right angle.
=> BE = $\frac{7}{2}=3.5$ cm and AE = $\frac{24}{2}=12$ cm
Thus, in right $\triangle$ AEB,
=> $(AB)^2=(AE)^2+(BE)^2$
=> $(AB)^2=(12)^2+(3.5)^2$
=> $(AB)^2=144+12.25=156.25$
=> $AB=\sqrt{156.25}=12.5$ cm
$\therefore$ Perimeter of rhombus ABCD = $4\times12.5=50$ cm
=> Ans – (D)
5) Answer (D)
Radius of cone, $r=\frac{21}{2}=10.5$ cm and slant height, $l=11$ cm
Total surface area of cone = $\pi r(l+r)$
= $\frac{22}{7}\times10.5\times(10.5+11)$
= $33\times21.5=709.5$ $cm^2$
=> Ans – (D)
6) Answer (B)
Radius of circle = $r=17.5$ cm
=> Area = $\pi r^2$
= $\frac{22}{7}\times17.5\times17.5$
= $22\times2.5\times17.5=962.5$ $cm^2$
=> Ans – (B)
7) Answer (A)
Let side of equilateral triangle = $s$ cm
=> Area = $\frac{\sqrt3}{4} s^2=25\sqrt3$
=> $\frac{s^2}{4}=25$
=> $s^2=25\times4=100$
=> $s=\sqrt{100}=10$ cm
=> Ans – (A)
8) Answer (D)
Length, $l=10.5$ cm, breadth, $b=8$ cm and height, $h=9$ cm
Total surface area of cuboid = $2(lb+bh+hl)$
= $2[(10.5\times8)+(8\times9)+(9\times10.5)]$
= $2\times(84+72+94.5)$
= $2\times250.5=501$ $cm^2$
=> Ans – (D)
9) Answer (C)
Let the length of rectangle = $l$ cm and breadth, $b=10$ cm
=> Diagonal, $d^2=l^2+b^2$
=> $l^2=(26)^2-(10)^2$
=> $l^2=676-100=576$
=> $l=\sqrt{576}=24$ cm
$\therefore$ Area = $24\times10=240$ $cm^2$
=> Ans – (C)
10) Answer (D)
Height of cylinder, $h=14$ cm and radius, $r=\frac{42}{2}=21$ cm
Total surface area of cylinder = $2\pi r(r+h)$
= $2\times\frac{22}{7}\times21\times(21+14)$
= $132\times35=4620$ $cm^2$
=> Ans – (D)
We hope this Mensuration Questions blog will definitely help at the time of your preparation. Download the cracku app for daily test.





