Trigonometry Questions for RRB NTPC Set-2 PDF
Download RRB NTPC Trigonometry Questions and Answers PDF. Top 15 RRB NTPC Maths questions based on asked questions in previous exam papers very important for the Railway NTPC exam.
Download Trigonometry Questions for RRB NTPC Set-2 PDF
Take a free mock test for RRB NTPC
Download RRB NTPC Previous Papers PDF
Question 1: Find cosecθ, if Cotθ = 40/9 ?
a) 9/41
b) 41/9
c) 41/40
d) 9/40
Question 2: Find the area of a triangle, whose inradius is 2 cm and ex-radii are 4cm, 8cm, 4 cm ?
a) 16 sq.cm
b) 17 sq.cm
c) 18 sq.cm
d) 19 sq.cm
Question 3: $1+Tan^2A$ = ?
a) $Cosec^2A$
b) $Sin^2A$
c) $Sec^2A$
d) $Cos^2A$
RRB NTPC Previous Papers [Download PDF]
Question 4: Find secθ, if sinθ = 21/29 ?
a) 21/20
b) 29/21
c) 20/21
d) 29/20
Question 5: Find cosθ-secθ, if cotθ = 15/8 ?
a) -64/255
b) 64/255
c) -64/289
d) 64/289
Question 6: Find the angle of elevation of the Sun if the length of shadow of a pole of height $70\sqrt3 cm$ is 70 cm ?
a) 90°
b) 60°
c) 45°
d) 30°
Question 7: Find $sec\theta-tan\theta$, if $sec\theta+tan\theta=2$ ?
a) 1/2
b) -2
c) 1
d) -1
Question 8: Find $cosec\theta$, if $cot\theta = 12/5$ ?
a) 5/13
b) 13/5
c) 12/13
d) 13/12
Question 9: Find $\frac{1-cos\frac{\theta}{2}}{sin\frac{\theta}{2}}$ = ?
a) $tan\frac{\theta}{4}$
b) $cot\frac{\theta}{2}$
c) $tan\frac{\theta}{2}$
d) $cot\frac{\theta}{4}$
Question 10: If $\tan A = \frac{5}{12}$, find the value of $\cosec A$. (Angle A is an acute angle)
a) 1.2
b) 2.6
c) $\frac{24}{5}$
d) 2.4
Question 11: If tan 330° = x, then the value of x is
a) $\frac{-1}{\sqrt{3}}$
b) ${-\sqrt{3}}$
c) $\frac{-1}{2}$
d) $\frac{-1}{\sqrt{2}}$
Download General Science Notes PDF
Question 12: In which of the following quadrilaterals only one pair of opposite angles is supplementary?
a) Isosceles Trapezium
b) Parallelogram
c) Cyclic quadrilateral
d) Rectangle
Question 13: If √$(1 – cos^2A)$ = x, then the value of x is
a) cosecA
b) sinA
c) tanA
d) secA
Question 14: If √$(sec^2A-1)/secA$ = x, then the value of x is
a) cosecA
b) cosA
c) sinA
d) tanA
Question 15: What is the value of $(sinA-2sin^3A)/(2cos^3A-cosA)$?
a) cotA
b) cosecA
c) secA
d) tanA
RRB NTPC Previous Papers (Download PDF)
Answers & Solutions:
1) Answer (B)
Cotθ = $\frac{adj}{opp}$ = 40/9
Cosecθ = $\frac{hyp}{opp}$ = 41/9 ($\because 40^2+9^2 = 41^2$)
So the answer is option B.
2) Answer (A)
If $ r$ is the inradius and $r_1,r_2,r_3$ are the radii of excircles, then area of triangle = $\sqrt{rr_1r_2r_3} = \sqrt{2*4*8*4} = \sqrt{256} = 16$
So the answer is option A.
3) Answer (C)
$1+Tan^2A$ = $Sec^2A$ ($\because Sec^2A-Tan^2A = 1$)
or
$1+Tan^2A$ = $1+\frac{Sin^2A}{Cos^2A}$ = $\frac{Cos^2A+Sin^2A}{Cos^2A}$ = $\frac{1}{Cos^2A}$ = $Sec^2A$
So the answer is option C.
4) Answer (D)
Sinθ = $\frac{opp}{hyp}$ = 21/29
Cosθ = $\frac{adj}{hyp}$ = 20/29 ($\because 20^2+21^2 = 29^2$)
secθ = 29/20
So the answer is option D.
5) Answer (A)
Cotθ = $\frac{adj}{opp}$ = 15/8
Cosθ = $\frac{adj}{hyp}$ = 15/17 ($\because 15^2+8^2 = 17^2$)
cosθ-secθ = 15/17 – 17/15 = (225-289)/(255) = -64/255
So the answer is option A.
6) Answer (B)
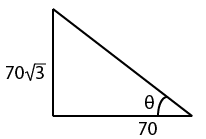
From the diagram, Tanθ = $\frac{70\sqrt3}{70} = \sqrt3$ = Tan60°
==> θ = 60°
So the answer is option B.
7) Answer (A)
We Know That, $(sec^2(\theta)-tan^2(\theta)) = 1$
Applying square on both sides,
$(sec^2(\theta)-tan^2(\theta))^2 = 1$
$[sec\theta-tan\theta][sec\theta+tan\theta] = 1$
$[sec\theta-tan\theta][2] = 1$
$[sec\theta-tan\theta] = 1/2$
So the answer is option A.
8) Answer (B)
$cot\theta = 12/5$
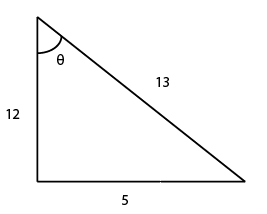
from the diagram,
$Cosec\theta$ = $\frac{ hypotenuse}{ opposite side} = \frac{13}{5}$
So the answer is option B.
9) Answer (A)
$\frac{1-cos\frac{\theta}{2}}{sin\frac{\theta}{2}}$
= $\frac{2sin^2\frac{\theta}{4}}{2sin\frac{\theta}{4}cos\frac{\theta}{4}}$
= $\frac{sin\frac{\theta}{4}}{cos\frac{\theta}{4}}$
= $tan\frac{\theta}{4}$
So the answer is option A.
10) Answer (B)
Given, $\tan A = \frac{5}{12}$.
Also, A is an cute angle.
We can consider a right triangle with the legs 5x and 12x; and
Hypotenuse = $\sqrt{(5x)^2 + (12x)^2}$ = 13x.
$\cosec A = \frac{13}{5} = 2.6$
Hence, option B is the correct answer.
11) Answer (A)
Expression : tan 330° = x
= $tan(360-30)$
= $-tan(30)$
= $\frac{-1}{\sqrt{3}}$
=> Ans – (A)
12) Answer (C)
In rectangle, all angles are 90° and in a parallelogram, adjacent angles are supplementary while in a cyclic quadrilateral only one pair of opposite angles is supplementary.
=> Ans – (C)
13) Answer (B)
Expression : $\sqrt{1-cos^2A}$
$\because (sin^2A+cos^2A=1)$
= $\sqrt{sin^2A}=sinA$
=> Ans – (B)
14) Answer (C)
Expression : $\frac{\sqrt{sec^2A-1}}{secA}$
$\because$ $(sec^2A-tan^2A=1)$
= $\frac{\sqrt{tan^2A}}{secA} = \frac{tanA}{secA}$
= $(\frac{sinA}{cosA})\div(\frac{1}{cosA})$
= $(\frac{sinA}{cosA})\times(cosA) = sinA$
=> Ans – (C)
15) Answer (D)
Expression : $(sinA-2sin^3A)/(2cos^3A-cosA)$
= $\frac{sinA}{cosA} \times \frac{1-2sin^2A}{2cos^2A-1}$
$\because$ $(sin^2A+cos^2A=1)$
= $tanA \times \frac{(sin^2A+cos^2A)-2sin^2A}{2cos^2A-(sin^2A+cos^2A)}$
= $tanA \times \frac{cos^2A-sin^2A}{cos^2A-sin^2A}$
= $tanA \times 1 = tanA$
=> Ans – (D)
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Trigonometry Questions set-2 pdf for RRB NTPC Exam will be highly useful for your Preparation.





