Trigonometry for SSC CGL:
Trigonometry is an extension of Geometry. It deals with the properties of angles of a triangle (Right angled triangle). We can split even non-right angled triangles into 2 right-angled triangles. Hence, the scope and application of Trigonometry for SSC CGL is enormous.
SSC has consistently asked around 10 questions from trigonometry in the tier 2 exam. Combined with geometry and mensuration, these topics hold the lion’s share in this section. Hence, it is quite essential to prepare well for this section.
100 SSC CGL (latest pattern mocks) – Rs. 199
SSC CGL Free Study Material – 18000 Questions
Aspirants can prepare for SSC CGL online to enhance their scores.
Since geometry forms the bedrock of Trigonometry for SSC CGL, aspirants can read geometry for SSC CGL to get an idea. Remember, one must have a decent grasp of geometry to understand the basics of trigonometry.
Trigonometry for SSC CGL is one of the most dreaded sections by banking aspirants.
Since they are alien to geometry and allied topics, some amount of effort is needed on their side as they have to start preparing from scratch.
Banking aspirants should not avoid geometry and other such topics as they form a sizable chunk of the question paper.
Aspirants can take mock tests for SSC CGL to gauge their level of preparedness. After covering the basics and practising enough, aspirants must take previous year papers of SSC CGL to get acquainted with the test.
SSC even repeats some questions from the previous year papers. Hence, practising previous year papers becomes all the more important.
How to prepare Trigonometry for SSC CGL Exam
Trigonometry for SSC CGL can be broadly divided into 2 sub-categories based on the questions.
1.Pure identity-based questions
2.Application based questions
Pure identity-based questions:
One can solve these questions only if he/she is thorough with the identities.
Download SSC CGL Maths Formulas PDF
However, it is not necessary to by heart tonnes of formulae. Study the basic Pythagorean identities.
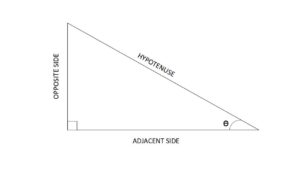
$$\sin\theta = \frac{opposite side}{hypotenuse}$$
$$\cos\theta = \frac{adjacent side}{hypotenuse}$$
$$\tan\theta = \frac{opposite side}{adjacent side}$$
$$tan\theta =\frac{sin\theta}{cos\theta}$$
$$cosec\theta = \frac{1}{sin\theta}$$
$$sec\theta = \frac{1}{cos\theta}$$
$$cot\theta = \frac{1}{tan\theta}$$
$$sin^{2}\theta + cos^{2}\theta = 1$$
$$tan^{2}\theta + 1 = sec^{2}\theta$$
$$cot^{2}\theta + 1 = cosec^{2}\theta$$
$$cos (A-B)= cos A cos B + sinA sin B$$
$$cos (A+B)= cos A cos B – sinA sin B$$
$$sin (A+B) = sin A cos B + cos A sin B$$
$$sin (A-B) = sin A cos B – cos A sin B$$
$$sin2A = 2 sin A cos A$$
The values of angles and their corresponding sin and cos values are very important. One can derive the other values from this table.
| 0o | 30o | 45o | 60o | 90o | |
| Sin | $$0$$ | $$\frac{1}{2}$$ | $$\frac{1}{\sqrt{2}}$$ | $$\frac{\sqrt{3}}{2}$$ | $$1$$ |
| Cos | $$1$$ | $$\frac{\sqrt{3}}{2}$$ | $$\frac{1}{\sqrt{2}}$$ | $$\frac{1}{2}$$ | $$0$$ |
| Tan | $$0$$ | $$\frac{1}{\sqrt{3}}$$ | $$1$$ | $$\sqrt{3}$$ | $$Undefined$$ |
Apart from these, study other basic identities.
$$sin(-\theta)=-sin\theta$$
$$cos(-\theta)=cos\theta$$
Most of the questions can be solved using these basic identities.
Use mnemonics such as All Silver Tea Cups to remember the polarity of various functions in various quadrants.
Here, SSC asks questions based on the application of the basic identities. Usually, these questions are of a hybrid type. SSC blends Geometry and trigonometry topics in these questions.
Download SSC CGL 2018 Syllabus PDF
Application based questions:
SSC asks questions on common topics like ladder slipping against a wall, moving towards/away from the pole, the angle of depression/elevation, towers, etc.
These questions are comparatively easier and interesting to solve than the pure identity-based questions. However, one must have a reasonable grasp on geometry to answer these questions.
Tips to solve problems on Trigonometry for SSC CGL:
Don’t go on a mugging spree:
By-heart only the basic identities. You can derive the other identities from them. Don’t mug up hundreds of formulae. Keep your list as short as possible.
Focus on areas that matter the most. Also, be thorough with the table of values.
Think laterally:
Plugging in the values solves most of the questions easily. Solve questions using the options. Don’t be confined to solving the questions only using the identities. Remember, Street smartness gets rewarded too.
Also, make constructions to solve certain problems. Try to solve them without using the identities. Doing so will enhance your ability to connect the dots.
SSC CGL Solved Previous papers
You can read our blog on quantitative aptitude for SSC CGL to get an overview of the entire section.
Read about Reasoning tips for SSC CGL exam.






[…] Trigonometry […]