Contents
Geometry for SSC CGL exam
Geometry is one of the most important, scoring, and, at the same time, most dreaded topics of SSC CGL exam. Quantitative Ability (QA) forms about 25% of the SSC CGL paper in both Tier I and Tier II. In Quant, Geometry for SSC CGL forms around 20% of the quant section in both these paper. Hence the importance of Geometry for SSC CGL 2018 is self-explanatory and needs no illustrious introduction. You can do your SSC CGL preparation online at your pace and comfort.
Even though Geometry Questions for SSC CGL are very important, students often overlook it because of the vastness of the syllabus. Moreover, Geometry for SSC CGL 2018 is mere a slight extension of the concepts we have learnt till Class X. Therefore, if approached in a systematic manner, this topic can be easily mastered in a matter of months.
100 SSC CGL (latest pattern mocks) – Rs. 199
SSC CGL Free Study Material – 18000 Questions
The other mistake that most of the students make is not attempting Previous years papers for SSC CGL and enough Mock tests for SSC CGL before appearing in the final exams. Remember, the skill set that you will develop by practising questions will only help up to a certain. Therefore, coming up with different test taking strategies and fine-tuning them by taking mock tests will help you maximize your score.
How to prepare Geometry for SSC CGL Exam:
The questions from Geometry can be classified into the following six broad figure types-
(i) Parallel Lines
The questions from this subsection are the easiest of all. In addition to it, there are very few properties that one needs to remember to be able to solve questions based on parallel lines.
Consider the following figure:
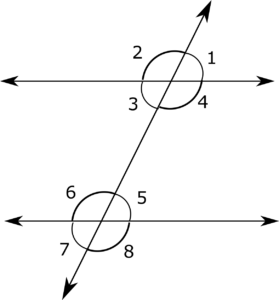
Here line 1 and line 2 are parallel to each other, and line three intersect them forming eight different angles as labelled in the figure.
Here,
$\angle 1 = \angle 5$, $\angle 2 = \angle 6$, $\angle 3 = \angle 7$, and $\angle 4 = \angle 8$ and these angles are called as pair of Corresponding angles.
Similarly, $\angle 3 = \angle 5$, $\angle 4 = \angle 6$, $\angle 1 = \angle 7$, and $\angle 2 = \angle 8$ and these angles are called as pair of Alternate angles.
$\angle 1 = \angle 3$, $\angle 2 = \angle 4$, $\angle 6 = \angle 8$, and $\angle 5 = \angle 7$ and these angles are called pair of Opposite angles.
Sum of interior angles on the same side of the transversal = Sum of exterior angles on the same side of transversal = $180^{\circ}$
=> $\angle 1 + \angle 8 = \angle 2 + \angle 7 = \angle 3 + \angle 6 = \angle 4 + \angle 5 = 180^{\circ}$
Most of the questions based on parallel lines are based on these theorems or combination of these theorems.
Download SSC CGL Maths Formulas PDF
(ii) Triangle
Questions based on Triangles and Circles are most frequently asked in Geometry for SSC CGL.
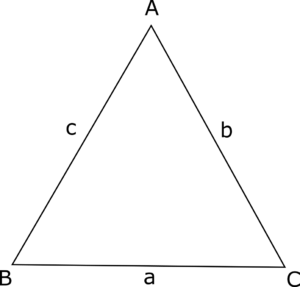
Some of the most commonly used properties of Triangles are-
- Sum of the interior angles of a triangle = $180^{\circ}$
- Area of triangle = $\frac{1}{2} \times h \times b$, where h = length of the height and b = length of the base
- Area of triangle = $\frac{1}{2} \times a \times b \times sin (\Theta)$, where a and b are two sides of the triangle, and $\Theta$ is the angle formed between these sides
- Area of triangle [Heron’s Formula]: $A = \sqrt{s(s-a)(s-b)(s-c)}$, where a, b, and c are the sides of the triangle and s = semiperimeter and $s = \frac{a+b+c}{2}$
- Area of an Equilateral Triangle = $\frac{\sqrt{3}a^2}{4}$, where ‘a’ is the side of the Equilateral Triangle.
- Pythagoras Theorem: In a right angled triangle ABC, right angled at B then,
$AC^2 = \sqrt{AB^2 + BC^2}$ - Incircle: Incircle is the circle that is perfectly inscribed in a triangle.
- Radius of incircle = $\frac{\text{Area of the triangle}}{\text{Semiperimeter of the triangle}}$
- Congruency of Triangles
- Similarity of Triangles
- Properties related to Median, Angle Bisector, Centroid, Incentre, Circumcentre, etc.
Download SSC CGL Important Questions PDF
(iii) Circle
As mentioned earlier, questions based on circles are frequently asked in Geometry for SSC CGL exam.
Some of the most frequently used properties of Circles are:
- Area of Circle = $\pi r^2$, where ‘r’ is the radius of the circle
- Perimeter of the circle = $2 \pi r$, where ‘r’ is the radius of the circle
- Length of an arc = $\frac{\Theta}{360} \times 2 \pi r $, where $\Theta$ is the angle subtended by the arc on the centre of the circle
- Area of a segment = $\frac{\Theta}{360} \times \pi r^2 $, where $\Theta$ is the angle subtended by the segment on the centre of the circle
- The perpendicular from the centre of a circle to a chord bisects the chord
- Perpendicular Bisector of two chords intersect at the centre
- Angle subtended by a chord at the centre is double the angle subtended by the chord at any point on the circle
- Angle in the same segment are equal
- The sum of opposite angles in a cyclic quadrilateral = $180^{\circ}$
- Angle inscribed in a semicircle is always $90^{\circ}$
- Equal chords are equidistant from the centre
- Equal chords subtend equal angles at the centre
- A tangent is always perpendicular to the radius of the circle
- Two tangents drawn from a point on a circle are equal in length
Many questions based on Circles also involve properties of triangles. Thus, it is very important for an aspirant to be thorough with all the subtopics of Geometry for SSC CGL.
(iv) Quadrilateral
A quadrilateral is a four-sided closed figure which has the sum of its interior angle as $180^{\circ}$.
The most common quadrilateral figures are Parallelogram, Rectangle, Square, Rhombus, and Trapezium.
Download SSC CGL 2018 Syllabus PDF
Parallelogram:
A parallelogram is a quadrilateral which is formed by two pairs of parallel lines.
Thus, all the parallel line properties that we just studied applies to this figure. Further, in a parallelogram-
- The diagonal bisects the figure into two congruent triangles.
- The diagonals bisect each other.
- Area of a parallelogram = Base X Height
Rectangle:
Square is a specific parallelogram where the consecutive sides are perpendicular to each other.
In a rectangle-
- Area = Length X Breadth
- Perimeter = 2 (Length + Breadth)
- Diagonals are equal and bisect each other
- Opposite sides are equal
- Line segments joining the midpoints of each side forms a rhombus
SSC CGL Solved Previous papers
Square:
Square is a specific rectangle where all sides are equal.
In a square-
- Area = Side$^2$
- Perimeter = 4 X Side
- Diagonals are equal and bisect each other perpendicularly
- Diagonals are angle bisector
Rhombus:
A rhombus is a parallelogram where all sides are equal.
In a Rhombus-
- All sides are equal
- Diagonals are NOT equal
- Diagonals intersect perpendicularly
- Area = $\frac{1}{2} \times \text{product of the diagonals}$
- Perimeter = 4 X Side
- Line segment joining the midpoints of each side forms a rectangle
Trapezium:
A trapezium is a quadrilateral in which one pair of opposite sides are parallel.
The area of a Trapezium is-
$Area =\frac{1}{2} \times \text{Height} \times \text{Sum of the parallel side}$
(v) Mensuration
This involves questions based on Volumes and Surface Areas of 3D Figures such as Cubes, Cuboids, Cones, Spheres, Hemisphere, Cylinders, Frustum, etc.
Mensuration questions are very easy and can be attempted with very high accuracy. As a result, remembering just a set of few formulas, students can attempt all such questions to maximize his/her score.
(vi) Heights and Distance
Heights and Distance is one such variety which is ever-present in all SSC CGL papers. Every SSC CGL paper has at least one question from this topic. By using the basic trigonometric ratios of $sin(\Theta)$, $cos(\Theta)$, $tan(\Theta)$ and the Pythagoras Theorem, most of the questions can be solved. Thus, it is one of those topics where you can attempt all the questions by understanding few properties.
[Note: This is not an exhaustive list of properties and theorems asked in SSC CGL examination. These are mentioned just to give you a fair idea of the syllabus of Geometry for SSC CGL]
Practice questions for SSC CGL Geometry
Once you are well versed with all the properties required to solve Geometry questions for SSC CGL, the next step is to solve as many questions as possible in the days leading up to the examination.
A lot of practice will help you in identifying the properties that might apply to a certain figure. Thus, you should make sure that you are thorough with all the theorems and properties so that they are at your disposal when required.
A good way to kick start your preparation is by taking Free Daily Tests for SSC CGL and Sectional Tests which will expose you to a wide variety of questions.
Mocks and Analysis- SSC Geometry
As I have mentioned earlier, one of the most crucial aspects of your preparation is taking and analysing a lot of mocks which most of the students overlook. Thus, even though they have a good knowledge of the subject, they are not able to maximize their scores in the test.
So, keep taking mocks at regular intervals and analyse them. This will help you in assessing your strengths and weaknesses. Thus, you will have a better idea of the kind of question you are good at and the kind of questions that you should probably attempt towards the end. Take a free SSC CGL mock test now.
Also, check out our excellent blogs on trigonometry for SSC CGL and how to prepare Quantitative aptitude for SSC exam






[…] Geometry […]
[…] aptitude section covers topics such as unitary methods, number systems, geometry, trigonometry, mensuration, algebra etc. Banking aspirants must prepare geometry, number systems […]