Top CAT DILR Questions PDF [Most Important With solutions]

Download DILR Questions for CAT PDF

Enroll for CAT 2022 Online Course

Instructions

DIRECTIONS for the following three questions: Answer the questions on the basis of the information given below.

Five friends meet every morning at Sree Sagar restaurant for an idli-vada breakfast. Each consumes a different number of idlis and vadas. The number of idlis consumed are 1, 4, 5, 6, and 8, while the number of vadas consumed are 0, 1, 2, 4, and 6. Below are some more facts about who eats what and how much.

i. The number of vadas eaten by Ignesh is three times the number of vadas consumed by the person who eats four idlis.

ii. Three persons, including the one who eats four vadas eat without chutney.

iii. Sandeep does not take any chutney.

iv. The one who eats one idli a day does not eat any vadas or chutney. Further, he is not Mukesh.

v. Daljit eats idli with chutney and also eats vada.

vi. Mukesh, who does not take chutney, eats half as many vadas as the person who eats twice as many idlis as he does.

vii. Bimal eats two more idlis than Ignesh, but Ignesh eats two more vadas than Bimal.

Question 1: Which one of the following statements is true?

a) Daljit eats 5 idlis

b) Ignesh eats 8 idlis

c) Bimal eats 1 idli.

d) Bimal eats 6 idlis.

1) Answer (A)

View Video Solution

Solution:

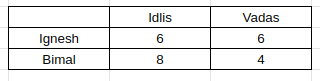
Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.

Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.

Using (vii), Bimal eats 2 more idlis than Ignesh.

Possibilities:

Bimal – 8, Ignesh – 6

Bimal – 6, Ignesh – 4

But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.

Hence we take Bimal – 8 and Ignesh – 6.

Also, we get that Bimal eats 6 – 2 = 4 vadas.

So far, we get the following information.

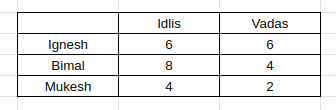
Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.

So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get

Daljit also eats Vada as per info (v), so we get the following

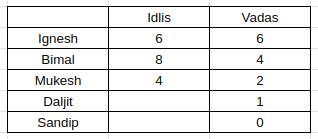
(iv) gives us the information that the one who eats 1idli does not have vada.

Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).

Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.

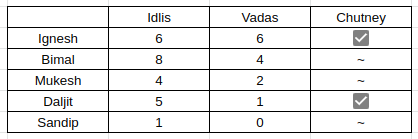
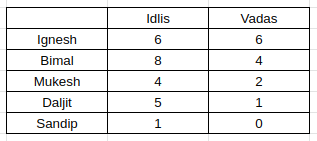
Option A, stating that Daljit eats 5 idlis, is right.

Question 2: Which of the following statements is true?

a) Sandeep eats 2 vadas.

b) Mukesh eats 4 vadas.

c) Ignesh eats 6 vadas.

d) Bimal eats 2 vadas.

2) Answer (C)

View Video Solution

Solution:

Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.

Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.

Using (vii), Bimal eats 2 more idlis than Ignesh.

Possibilities:

Bimal – 8, Ignesh – 6

Bimal – 6, Ignesh – 4

But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.

Hence we take Bimal – 8 and Ignesh – 6.

Also, we get that Bimal eats 6 – 2 = 4 vadas.

So far, we get the following information.

Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.

So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get

Daljit also eats Vada as per info (v), so we get the following

(iv) gives us the information that the one who eats 1idli does not have vada.

Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).

Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.

Hence, Ignesh eats 6 Vadas.

Question 3: Which of the following statements is true?

a) Mukesh eats 8 idlis and 4 vadas but no chutney.

b) The person who eats 5 idlis and 1 vada does not take chutney.

c) The person who eats equal number of vadas and idlis also takes chutney.

d) The person who eats 4 idlis and 2 vadas also takes chutney.

3) Answer (C)

View Video Solution

Solution:

Considering (i), Ignesh has to eat 6 vadas, since 6 is the only multiple of 3.

Also, using the same information, we can say that a person consumes 2 vadas and 4 idlis.

Using (vii), Bimal eats 2 more idlis than Ignesh.

Possibilities:

Bimal – 8, Ignesh – 6

Bimal – 6, Ignesh – 4

But Ignesh cannot have 4 idlis because the person who eats 4 idlis eats 2 vadas.

Hence we take Bimal – 8 and Ignesh – 6.

Also, we get that Bimal eats 6 – 2 = 4 vadas.

So far, we get the following information.

Using (vi), there is a person who eats twice as many idlis as Mukesh. The only pair satisfying is 8, 4.

So, Mukesh eats 4 idlis. Plus the person who eats 4 idlis eats 2 vadas. Hence, we get

Daljit also eats Vada as per info (v), so we get the following

(iv) gives us the information that the one who eats 1idli does not have vada.

Considering the persons who had chutney and those who didn’t, 3 persons do not have chutney. Bimal is one of them(the one eating 4 vadas).

Mukesh is the second one to not take chutney(last hint). Also, Sandip does not take chutney. Hence, we get this information as well.

Hence, Ignesh eating 6 vadas and 6 idlis eat Chutney.

Download CAT Previous Papers PDF

Instructions

There were seven elective courses – E1 to E7 – running in a specific term in a college. Each of the 300 students enrolled had chosen just one elective from among these seven. However, before the start of the term, E7 was withdrawn as the instructor concerned had left the college. The students who had opted for E7 were allowed to join any of the remaining electives. Also, the students who had chosen other electives were given one chance to change their choice. The table below captures the movement of the students from one elective to another during this process. Movement from one elective to the same elective simply means no movement. Some numbers in the table got accidentally erased; however, it is known that these were either 0 or 1.

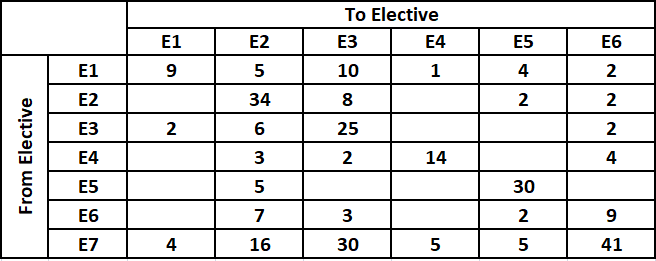
Further, the following are known:
1. Before the change process there were 6 more students in E1 than in E4, but after the reshuffle, the number of students in E4 was 3 more than that in E1.
2. The number of students in E2 increased by 30 after the change process.
3. Before the change process, E4 had 2 more students than E6, while E2 had 10 more students than E3.

Question 4: How many elective courses among E1 to E6 had a decrease in their enrollments after the change process?

a) 4

b) 1

c) 2

d) 3

4) Answer (C)

View Video Solution

Solution:

From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.

It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 – 30 = 46.

It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 – 10 = 36.

Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle =  9 + 5 + 10 + 1 + 4 + 2 = 31.

It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 – 6 = 25.

Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle =  25 – 2 = 23.

All the students from E7 moved to one of electives among E1 to E6.
Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.

Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.

Hence, the the number of students who were enrolled in E7 before reshuffle = 300 – (46+36+31+25+23+101) = 38.

For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.

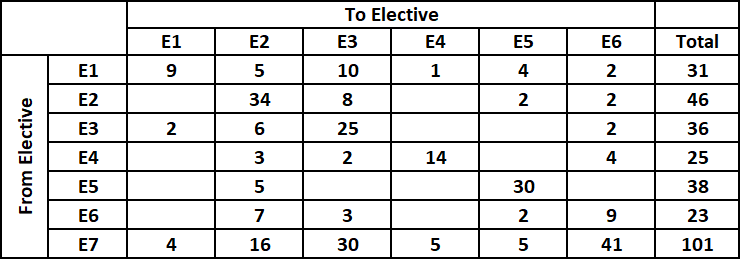
For elective E2,

Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46

i.e. Number of students who moved from to E1 =  Number of students who moved from to E4 = 0

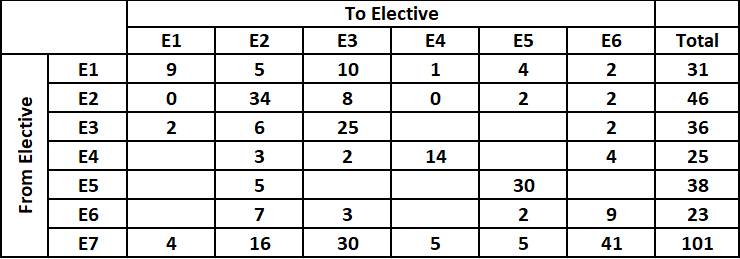
For elective E4,

Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25

i.e. Number of students who moved from to E1 =  Number of students who moved from to E5 = 1     {As the remaining blanks can be filled by either 0 or 1}

For elective E6,

Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23

i.e. Number of students who moved from to E1 =  Number of students who moved from to E4 = 1     {As the remaining blanks can be filled by either 0 or 1}

It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1.
As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 +  E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}

Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4  = 17 + E5 to E1.

Hence, it is possible only when  E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.

Remaining blank places can be filled easily as we know the total sum of each row.

Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.

Form the table we can see that the number of students who enrolled for E1 and E4 decreased from 31 and 25 to 18 and 21 respectively.

Therefore, option C is the correct answer.

Question 5: After the change process, which of the following is the correct sequence of number of students in the six electives E 1 to E6?

a) 19, 76, 79, 21, 45, 60

b) 19, 76, 78, 22, 45, 60

c) 18, 76, 79, 23, 43, 61

d) 18, 76, 79, 21, 45, 61

5) Answer (D)

View Video Solution

Solution:

From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.

It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 – 30 = 46.

It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 – 10 = 36.

Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle =  9 + 5 + 10 + 1 + 4 + 2 = 31.

It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 – 6 = 25.

Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle =  25 – 2 = 23.

All the students from E7 moved to one of electives among E1 to E6.
Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.

Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.

Hence, the the number of students who were enrolled in E7 before reshuffle = 300 – (46+36+31+25+23+101) = 38.

For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.

For elective E2,

Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46

i.e. Number of students who moved from to E1 =  Number of students who moved from to E4 = 0

For elective E4,

Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25

i.e. Number of students who moved from to E1 =  Number of students who moved from to E5 = 1     {As the remaining blanks can be filled by either 0 or 1}

For elective E6,

Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23

i.e. Number of students who moved from to E1 =  Number of students who moved from to E4 = 1     {As the remaining blanks can be filled by either 0 or 1}

It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1.
As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 +  E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}

Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4  = 17 + E5 to E1.

Hence, it is possible only when  E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.

Remaining blank places can be filled easily as we know the total sum of each row.

Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.

Form the table, we can see that after the reshuffle the number of students in electives E1 to E6 are 18, 76, 79, 21, 45 and 61 in that order.

Therefore, option D is the correct answer.

Checkout: CAT Free Practice Questions and Videos

Question 6: After the change process, which course among E1 to E6 had the largest change in its enrollment as a percentage of its original enrollment?

a) E1

b) E2

c) E3

d) E6

6) Answer (D)

View Video Solution

Solution:

From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.

It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 – 30 = 46.

It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 – 10 = 36.

Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle =  9 + 5 + 10 + 1 + 4 + 2 = 31.

It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 – 6 = 25.

Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle =  25 – 2 = 23.

All the students from E7 moved to one of electives among E1 to E6.
Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.

Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.

Hence, the the number of students who were enrolled in E7 before reshuffle = 300 – (46+36+31+25+23+101) = 38.

For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.

For elective E2,

Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46

i.e. Number of students who moved from to E1 =  Number of students who moved from to E4 = 0

For elective E4,

Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25

i.e. Number of students who moved from to E1 =  Number of students who moved from to E5 = 1     {As the remaining blanks can be filled by either 0 or 1}

For elective E6,

Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23

i.e. Number of students who moved from to E1 =  Number of students who moved from to E4 = 1     {As the remaining blanks can be filled by either 0 or 1}

It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1.
As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 +  E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}

Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4  = 17 + E5 to E1.

Hence, it is possible only when  E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.

Remaining blank places can be filled easily as we know the total sum of each row.

Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.

We are asked the largest change in its enrollment as a percentage of its original enrollment for all 6 electives but as we can see there are only 4 electives. Hence, we will check only for E1, E2, E3 and E6.

The percentage change in the number of students for E1 = $\dfrac{18-31}{31}\times 100$ $\approx$ 42 %

The percentage change in the number of students for E2 = $\dfrac{76-46}{46}\times 100$ $\approx$ 65 %

The percentage change in the number of students for E3 = $\dfrac{79-36}{36}\times 100$ $\approx$ 119 %

The percentage change in the number of students for E6 = $\dfrac{61-23}{23}\times 100$ $\approx$ 165 %

We can see that the percent change in the number of student for E6 is the largest. Therefore, option D is the correct answer.

Question 7: Later, the college imposed a condition that if after the change of electives, the enrollment in any elective (other than E7) dropped to less than 20 students, all the students who had left that course will be required to re-enroll for that elective.
Which of the following is a correct sequence of electives in decreasing order of their final enrollments?

a) E2, E3, E6, E5, E1, E4

b) E3, E2, E6, E5, E4, E1

c) E2, E5, E3, E1, E4, E6

d) E2, E3, E5, E6, E1, E3

7) Answer (A)

View Video Solution

Solution:

From the table we can say that number of students who opted for E2 after reshuffle = 5 + 34 + 6 + 3 + 5 + 7 + 16 = 76.

It is given us that the number of students in E2 increased by 30 after the change process. Hence, we can say that the number of students who were enrolled in E2 before reshuffle = 76 – 30 = 46.

It is given that before the change process there were 10 more students in E2 than in E3. Therefore, the number of students who were enrolled in E3 before reshuffle = 46 – 10 = 36.

Number of students who moved from E1 to all other electives are known. Therefore, the number of students who were enrolled in E1 before reshuffle =  9 + 5 + 10 + 1 + 4 + 2 = 31.

It is given that before the change process there were 6 more students in E1 than in E4. Therefore, the number of students who were enrolled in E4 before reshuffle = 31 – 6 = 25.

Also, it is given that E4 had 2 more students than E6 before reshuffle. Therefore, the number of students who were enrolled in E6 before reshuffle =  25 – 2 = 23.

All the students from E7 moved to one of electives among E1 to E6.  Therefore, the number of students who were enrolled in E7 before reshuffle = 4 + 16 + 30 + 5 + 5 + 41 = 101.

Except E5 we know the number of students who were enrolled in all electives. We also know that there were total 300 students who opted for exactly 1 elective.

Hence, the the number of students who were enrolled in E7 before reshuffle = 300 – (46+36+31+25+23+101) = 38.

For each elective, the number of students who were enrolled before reshuffle will be same as sum of the number of students who moved from that elective to another elective including no movement cases.

For elective E2,

Number of students who moved to E1 + 34 + 8 + Number of students who moved to E4 + 2 + 2 = 46

i.e. Number of students who moved from to E1 =  Number of students who moved from to E4 = 0

For elective E4,

Number of students who moved to E1 + 3 + 2 + 14 + Number of students who moved to E5 + 4 = 25

i.e. Number of students who moved from to E1 =  Number of students who moved from to E5 = 1     {As the remaining blanks can be filled by either 0 or 1}

For elective E6,

Number of students who moved to E1 + 7 + 3 + Number of students who moved to E4 + 2 + 9 = 23

i.e. Number of students who moved from to E1 =  Number of students who moved from to E4 = 1     {As the remaining blanks can be filled by either 0 or 1}

It is given that after the reshuffle, the number of students in E4 was 3 more than that in E1. As of now the number of students enrolled in E4 after reshuffle = 1 + 0 + E3 to E4 + 14 +  E5 to E4 + 1 + 5 = 21 + {E3 to E4} + {E5 to E4}

Also, the number of students enrolled in E1 after reshuffle = 9 + 0 + 2 + 1 + E5 to E1 + 1 + 4  = 17 + E5 to E1.

Hence, it is possible only when  E5 to E1 = 1 and E3 to E4 = E5 to E4 = 0.

Remaining blank places can be filled easily as we know the total sum of each row.

Therefore, the number of students who moved from E3 to E5 = the number of students who moved from E5 to E3 = the number of students who moved from E5 to E6 = 1.

We can see from the table that number of students enrolled in E1 dropped to 18. Hence, all the students who moved from E1 to any other elective will have to re-enroll in E1.

We can see that the number of students who enrolled for E1 prior to reshuffle = 31. Out of these 31 students, 9 students didn’t move to any other elective whereas remaining 22 students moved to other electives. Hence, all these 22 students have to re-enroll in E1.

Therefore, the total number of students in E1 post re-enrollment = 18 + 22 = 40 which is shown in the table.

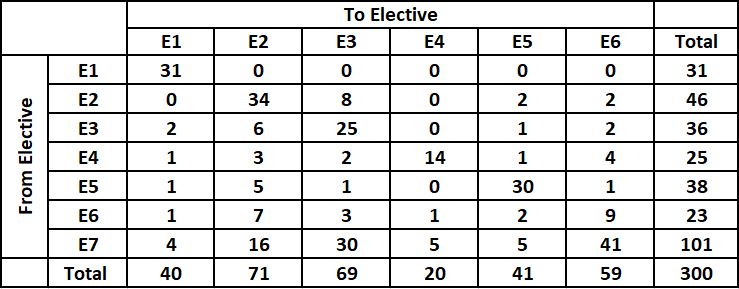
Therefore, the sequence of electives in decreasing order of their final enrollments = E2, E3, E6, E5, E1, E4.

Hence, option A is the correct answer.

Download CAT 2022 Detailed Syllabus PDF

Instructions

A high security research lab requires the researchers to set a pass key sequence based on the scan of the five fingers of their left hands. When an employee first joins the lab, her fingers are scanned in an order of her choice, and then when she wants to re-enter the facility, she has to scan the five fingers in the same sequence.
The lab authorities are considering some relaxations of the scan order requirements, since it is observed that some employees often get locked-out because they forget the sequence.

Question 8: The lab has decided to allow a variation in the sequence of scans of the five fingers so that at most two scans (out of five) are out of place. For example, if the original sequence is Thumb (T), index finger (I), middle finger (M), ring finger (R) and little finger (L) then TLMRI is also allowed, but TMRLI is not.
How many different sequences of scans are allowed for any given person’s original scan?

Question 9: The lab has decided to allow variations of the original sequence so that input of the scanned sequence of five fingers is allowed to vary from the original sequence by one place for any of the fingers. Thus, for example, if TIMRL is the original sequence, then ITRML is also allowed, but LIMRT is not.
How many different sequences are allowed for any given person’s original scan?

a) 7

b) 5

c) 8

d) 13

9) Answer (C)

View Video Solution

Solution:

Input of the scanned sequence of five fingers is allowed to vary from the original sequence by one place for any of the fingers. This can be achieved only when two consecutive fingers are interchanged. Let the original sequence be TIMRL
Case 1: Only a set of two consecutive numbers are interchanged.
They can be selected in 5-1 = 4 ways
Case 2: Two sets of two consecutive numbers are interchanged.
(i) TI are interchanged, => (MR, RL) => 2 ways
(ii) IM are interchanged => (RL) => 1 way
Total no of ways possible = 4 + 2 + 1 = 7

Including the original sequence, we get the total number of allowed combinations as 8

Question 10: The lab has now decided to require six scans in the pass key sequence, where exactly one finger is scanned twice, and the other fingers are scanned exactly once, which can be done in any order. For example, a possible sequence is TIMTRL.
Suppose the lab allows a variation of the original sequence (of six inputs) where at most two scans (out of six) are out of place, as long as the finger originally scanned twice is scanned twice and other fingers are scanned once.
How many different sequences of scans are allowed for any given person’s original scan?

Question 11: The lab has now decided to require six scans in the pass key sequence, where exactly one finger is scanned twice, and the other fingers are scanned exactly once, which can be done in any order. For example, a possible sequence is TIMTRL.
Suppose the lab allows a variation of the original sequence (of six inputs) so that input in the form of scanned sequence of six fingers is allowed to vary from the original sequence by one place for any of the fingers, as long as the finger originally scanned twice is scanned twice and other fingers are scanned once.
How many different sequences of scans are allowed if the original scan sequence is LRLTIM?

a) 8

b) 11

c) 13

d) 14

11) Answer (C)

View Video Solution

Solution:

1. If original sequence is given.

2. If either of LR, RL, LT, TI, IM is interchanged => 5 ways.

3. If LR and LT and IM interchanged. The sequence will look like: RLTLMI

4. If LR and LT are interchanged.

5. If LR and TI are interchanged.

6. If LR and IM are interchanged.

7. If RL and TI are interchanged.

8. If RL and IM  are interchanged.

9. If LT and IM are interchanged.

Total 13 ways possible.

Take 3 Free CAT Mocks Here

Instructions

Adriana, Bandita, Chitra, and Daisy are four female students, and Amit, Barun, Chetan, and Deb are four male students. Each of them studies in one of three institutes – X, Y, and Z. Each student majors in one subject among Marketing, Operations, and Finance, and minors in a different one among these three subjects. The following facts are known about the eight students:

1. Three students are from X, three are from Y, and the remaining two students, both female, are from Z.
2. Both the male students from Y minor in Finance, while the female student from Y majors in Operations.
3. Only one male student majors in Operations, while three female students minor in Marketing.
4. One female and two male students major in Finance.
5. Adriana and Deb are from the same institute. Daisy and Amit are from the same institute.
6. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.
7. Daisy minors in Operations.

Question 12: Who are the students from the institute Z?

a) Chitra and Daisy

b) Adriana and Bandita

c) Bandita and Chitra

d) Adriana and Daisy

12) Answer (C)

View Video Solution

Solution:

There are 8 students in total – 4 male and 4 female. There are 3 institutes X, Y, and Z.
3 students are from institute X, 3 students are from institute Y, and 2 students are from institute Z. No student majors and minors in the same subject.

It has been given that both the students from institute Z are female. Also, it has been given that both the male students from institute Y minor in Finance. Therefore, the third student from institute Y should be female. Institute X should also have 2 male and 1 female student.

Both the male students from Y minor in Finance, while the female student from Y majors in Operations. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.

It has been given that one female student and 2 male students major in finance. We know that the male student from Y minors in finance. Therefore, he cannot major in finance. Therefore, both the male students from X should major in finance.

Daisy and Amit are from the same institute. Therefore, Daisy cannot be from institute Z (since Amit is a male student and both the students from Z are female). Daisy minors in operations. The girl from institute Y majors in Operations. Therefore, Daisy cannot be from institute Y as well. Daisy and Amit should be from institute X. 3 female students minor in marketing. Therefore, all girls except Daisy should minor in marketing.

Adriana and Deb are from the same institute. Therefore, both of them should be from institute Y. Bandita and Chitra should be from institute Z.

Only one male student majors in Operations. We know that Barun is the student. Two male students major in Finance. We know that Amit and Chetan major in finance. Therefore, Deb should major in Marketing.

Bandita and Chitra are from institute Z. Therefore, option C is the right answer.

Question 13: Which subject does Deb minor in?

a) Operations

b) Finance

c) Marketing

d) Cannot be determined uniquely from the given information

13) Answer (B)

View Video Solution

Solution:

There are 8 students in total – 4 male and 4 female. There are 3 institutes X, Y, and Z.
3 students are from institute X, 3 students are from institute Y, and 2 students are from institute Z. No student majors and minors in the same subject.

It has been given that both the students from institute Z are female. Also, it has been given that both the male students from institute Y minor in Finance. Therefore, the third student from institute Y should be female. Institute X should also have 2 male and 1 female student.

Both the male students from Y minor in Finance, while the female student from Y majors in Operations. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.

It has been given that one female student and 2 male students major in finance. We know that the male student from Y minors in finance. Therefore, he cannot major in finance. Therefore, both the male students from X should major in finance.

Daisy and Amit are from the same institute. Therefore, Daisy cannot be from institute Z (since Amit is a male student and both the students from Z are female). Daisy minors in operations. The girl from institute Y majors in Operations. Therefore, Daisy cannot be from institute Y as well. Daisy and Amit should be from institute X. 3 female students minor in marketing. Therefore, all girls except Daisy should minor in marketing.

Adriana and Deb are from the same institute. Therefore, both of them should be from institute Y. Bandita and Chitra should be from institute Z.

Only one male student majors in Operations. We know that Barun is the student. Two male students major in Finance. We know that Amit and Chetan major in finance. Therefore, Deb should major in Marketing.

Deb minors in Finance. Therefore, option B is the right answer.

Question 14: Which subject does Amit major in?

a) Marketing

b) Operations

c) Cannot be determined uniquely from the given information

d) Finance

14) Answer (D)

View Video Solution

Solution:

There are 8 students in total – 4 male and 4 female. There are 3 institutes X, Y, and Z.
3 students are from institute X, 3 students are from institute Y, and 2 students are from institute Z. No student majors and minors in the same subject.

It has been given that both the students from institute Z are female. Also, it has been given that both the male students from institute Y minor in Finance. Therefore, the third student from institute Y should be female. Institute X should also have 2 male and 1 female student.

Both the male students from Y minor in Finance, while the female student from Y majors in Operations. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.

It has been given that one female student and 2 male students major in finance. We know that the male student from Y minors in finance. Therefore, he cannot major in finance. Therefore, both the male students from X should major in finance.

Daisy and Amit are from the same institute. Therefore, Daisy cannot be from institute Z (since Amit is a male student and both the students from Z are female). Daisy minors in operations. The girl from institute Y majors in Operations. Therefore, Daisy cannot be from institute Y as well. Daisy and Amit should be from institute X. 3 female students minor in marketing. Therefore, all girls except Daisy should minor in marketing.

Adriana and Deb are from the same institute. Therefore, both of them should be from institute Y. Bandita and Chitra should be from institute Z.

Only one male student majors in Operations. We know that Barun is the student. Two male students major in Finance. We know that Amit and Chetan major in finance. Therefore, Deb should major in Marketing.

Amit majors in finance. Therefore, option D is the right answer.

Question 15: If Chitra majors in Finance, which subject does Bandita major in?

a) Finance

b) Cannot be determined uniquely from the given information

c) Operations

d) Marketing

15) Answer (C)

View Video Solution

Solution:

There are 8 students in total – 4 male and 4 female. There are 3 institutes X, Y, and Z.
3 students are from institute X, 3 students are from institute Y, and 2 students are from institute Z. No student majors and minors in the same subject.

It has been given that both the students from institute Z are female. Also, it has been given that both the male students from institute Y minor in Finance. Therefore, the third student from institute Y should be female. Institute X should also have 2 male and 1 female student.

Both the male students from Y minor in Finance, while the female student from Y majors in Operations. Barun is from Y and majors in Operations. Chetan is from X and majors in Finance.

It has been given that one female student and 2 male students major in finance. We know that the male student from Y minors in finance. Therefore, he cannot major in finance. Therefore, both the male students from X should major in finance.

Daisy and Amit are from the same institute. Therefore, Daisy cannot be from institute Z (since Amit is a male student and both the students from Z are female). Daisy minors in operations. The girl from institute Y majors in Operations. Therefore, Daisy cannot be from institute Y as well. Daisy and Amit should be from institute X. 3 female students minor in marketing. Therefore, all girls except Daisy should minor in marketing.

Adriana and Deb are from the same institute. Therefore, both of them should be from institute Y. Bandita and Chitra should be from institute Z.

Only one male student majors in Operations. We know that Barun is the student. Two male students major in Finance. We know that Amit and Chetan major in finance. Therefore, Deb should major in Marketing.

If Chitra majors in finance, Bandita cannot major in finance (only one female student majors in finance). She cannot major in marketing as well (since she has a minor degree in marketing). Therefore, Bandita should major in operations and hence, option C is the right answer.

Get Upto 50% Scholarship on CAT 2022 course

Instructions

Directions for the following four questions: Answer the questions on the basis of the information given below.

Twenty one participants from four continents (Africa, Americas, Australasia, and Europe) attended a United Nations conference. Each participant was an expert in one of four fields, labour, health, population studies, and refugee relocation. The following five facts about the participants are given.

(a) The number of labour experts in the camp was exactly half the number of experts in each of the three other categories.

(b) Africa did not send any labour expert. Otherwise, every continent, including Africa, sent at least one expert for each category.

(c) None of the continents sent more than three experts in any category.

(d) If there had been one less Australasian expert, then the Americas would have had twice as many experts as each of the other continents.

(e) Mike and Alfanso are leading experts of population studies who attended the conference. They are from Australasia.

Question 16: Which of the following combinations is NOT possible?

a) 2 experts in population studies from the Americas and 2 health experts from Africa attended the conference.

b) 2 experts in population studies from the Americas and 1 health expert from Africa attended the conference.

c) 3 experts in refugee relocation from the Americas and 1 health expert from Africa attended the conference.

d) Africa and America each had 1 expert in population studies attending the conference.

16) Answer (D)

View Video Solution

Solution:

According to given conditions, the possible solutions are as given in the tables below:

From the above tables we can see that there was no possible case in which Africa and America had 1 expert each in population studies. Thus, statement D is false.

Question 17: If Ramos is the lone American expert in population studies, which of the following is NOT true about the numbers of experts in the conference from the four continents?

a) There is one expert in health from Africa.

b) There is one expert in refugee relocation from Africa.

c) There are two experts in health from the Americas.

d) There are three experts in refugee relocation from the Americas.

17) Answer (C)

View Video Solution

Solution:

From the first condition a, assume the number of experts in labour = x, then the number of experts in each of the other three categories =2x
Now, x+2x+2x+2x+2x = 21  => x = 3 and 2x = 6
So the number of experts in labour = 3 and the number of experts in each of the three categories = 6
From condition d, if the number of experts of Astralaisa = y, then the number of experts of Americas = 2(y-1), the number of experts of Europe = y-1, the number of experts of Africa= y-1
Now, y+y-1+y-1+2(y-1)=21  => 5y-4=21  => y=5
Hence the table can be filled as follows:

Using condition b, the number of labour experts of Africa = 0 and the number of labour experts of the rest of the continents will be 1 each.
Consider the column of Europe, since Europe sent at least 1 in each category, each category will have 1 expert. (Since the total sum is 4)
From the condition e, the population studies of Australasia will contain 2 experts. So all the other categories will have to take at 1 expert because the total sum is 5 and no value can be 0. The table can be filled as follows:

Now, according to the condition c, the possible solutions are as given in the tables below:

From the tables we can see that when there is only 1 population expert from America, there are 3 American Health Experts. Hence option C is not true.

Question 18: Alex, an American expert in refugee relocation, was the first keynote speaker in the conference. What can be inferred about the number of American experts in refugee relocation in the conference, excluding Alex?
i. At least one
ii. At most two

a) Only i and not ii

b) Only ii and not I

c) Both i and ii

d) Neither i nor ii

18) Answer (C)

View Video Solution

Solution:

According to given conditions, the possible solutions are as given in the tables below:

If an American expert in refugee relocation, was the first keynote speaker in the conference. Then apart from him there is atleast 1 and atmost 2 american expert in refugee relocation. Hence option C.

Question 19: Which of the following numbers cannot be determined from the information given?

a) Number of labour experts from the Americas.

b) Number of health experts from Europe.

c) Number of health experts from Australasia.

d) Number of experts in refugee relocation from Africa.

19) Answer (D)

View Video Solution

Solution:

According to given conditions, the possible solutions are as given in the tables below:

We can see that there are 2 possibilities for number of experts in refugee relocation from Africa.Hence it cannot be determined.

CAT Data Interpretation Questions PDF

Instructions

Two traders, Chetan and Michael, were involved in the buying and selling Of MCS shares over five trading days. At the beginning of the first day, the MCS share was priced at Rs 100, while at the end of the fifth day it was priced at Rs 110. At the end of each day, the MCS share price either went up by Rs 10, or else, it came down by Rs 10. Both Chetan and Michael took buying and selling decisions at the end of each trading day. The beginning price of MCS share on a given day was the same as the ending price of the previous day. Chetan and Michael started with the same number of shares and amount of cash, and had enough of both. Below are some additional facts about how Chetan and Michael traded over the five trading days.

• Each day if the price went up, Chetan sold 10 shares of MCS at the closing price. On the other hand, each day if the price went down, he bought 10 shares at the closing price.

• If on any day, the closing price was above Rs 110, then Michael sold 10 shares of MCS, while if it was below Rs 90, he bought 10 shares, all at the closing price.

Question 20: If Chetan sold 10 shares of MCS on three consecutive days, while Michael sold 10 shares only once during the five days, what was the price of MCS at the end of day 3?

a) Rs 90

b) Rs 100

c) Rs 110

d) Rs 120

e) Rs 130

20) Answer (C)

View Video Solution

Solution:

The above table includes the values of the share price at the end of each day. Chetan and Michael column shows the number of shares at the end of 5th day with Chetan and Michael respectively. (-10 means he has sold 10 shares, +10 means he has bought 10 shares)

there are 10 different possible cases according to the initial and final share price.

The question asks about the case where Chetan has sold 3 times and Michael sells only once.

Starting with Michael, for exactly one sell, the price should touch 120 only once as Michael sells the share only at price greater than 110.

if the price touches 120 twice or more, Michael will sell the share more than once which is not a desirable case.

Also, chetan has to sell thrice consecutively which is only possible if the share price is 90 at one instance and rises to 120 in straight 3 days.

This is only possible in case 2. Hence the price on 3rd day’s end in case 2 is 110.

Question 21: If Michael ended up with Rs 100 less cash than Chetan at the end of day 5, what was the difference in the number of shares possessed by Michael and Chetan (at the end of day 5)?

a) Michael had 10 less shares than Chetan.

b) Michael had 10 more shares than Chetan.

c) Chetan had 10 more shares than Michael.

d) Chetan had 20 more shares than Michael.

e) Both had the same number of shares.

21) Answer (E)

View Video Solution

Solution:

The above table includes the values of the share price at the end of each day. Chetan and Michael column shows the number of shares at the end of 5th day with Chetan and Michael respectively. (-10 means he has sold 10 shares, +10 means he has bought 10 shares)

there are 10 different possible cases according to the initial and final share price.

Please note that Chetan will always be having -10 shares(10 shares sold) and 1300 as cash.

This is because Chetan buys for every fall in price and sells for every rise in price. But the fluctuation in share price is constant as it starts from 100 and closes at 110 on day 5. So, in total chetan will always sell 10 shares in all 5 days combined.

As chetan has sold 10 shares , he’ll get 110*10 =1100 cash because of it in every case. Also chetan earns Rs. 200 in every case because of buying at low and selling at high. So total cash chetan will always have after 5 days = 1100+200 =1300.

The question asks about the case where Michael ended up with Rs 100 less cash than Chetan at the end of day 5.

So we have to look for the case where Michael has 1200 cash which is only possible when Michael has -10 number of shares in the end of day 5 and also has made profit of Rs. 100.

This is possible in case 7 as Michael has sold the shares at rs 120 but did not sell those shares as price never went below 90.

In the end Michael will have -10 shares at a price 110 which is Rs. 10 less than the price he sold at.

So he makes profit of 100 rs through it and will have the cash of 1100 through the sold shares.
Their difference in 7th case is 1300-1200=100

Also, in this case they have same number of shares sold at the end of the 5th day. So E is the answer.

Question 22: If Chetan ended up with Rs 1300 more cash than Michael at the end of day 5, what was the price of MCS share at the end of day 4?

a) Rs 90

b) Rs 100

c) Rs 110

d) Rs 120

e) Not uniquely determinable

22) Answer (B)

View Video Solution

Solution:

The above table includes the values of the share price at the end of each day. Chetan and Michael column shows the number of shares at the end of 5th day with Chetan and Michael respectively. (-10 means he has sold 10 shares, +10 means he has bought 10 shares)

there are 10 different possible cases according to the initial and final share price.

Please note that Chetan will always be having -10 shares(10 shares sold) and 1300 as cash.

This is because Chetan buys for every fall in price and sells for every rise in price. But the fluctuation in share price is constant as it starts from 100 and closes at 110 on day 5. So, in total Chetan will always sell 10 shares in all 5 days combined.

As Chetan has sold 10 shares, he’ll get 110*10 =1100 cash because of it in every case. Also, Chetan earns Rs. 200 in every case because of buying at low and selling at high. So total cash Chetan will always have after 5 days = 1100+200 =1300.

The question asks about the case where Michael ended up with Rs 1300 cash less than Chetan.

As Chetan will have exactly 1300 cash in every case; we have to look for the cases where Michael does not make any profit and also does not have any sold shares at the end of 5 days.

This is possible in 4 cases ie. 3,4,5 and 9.

In each of these cases, the price fluctuates in the range 90-110 which does not allow Michael to buy or sell any shares.

Also, in all these cases the price of MCS is 100 at the end of day 4.

So the answer is 100.

Question 23: What could have been the maximum possible increase in combined cash balance of Chetan and Michael at the end of the fifth day?

a) Rs 3700

b) Rs 4000

c) Rs 4700

d) Rs 5000

e) Rs 6000

23) Answer (D)

View Video Solution

Solution:

The above table includes the values of the share price at the end of each day. Chetan and Michael column shows the number of shares at the end of 5th day with Chetan and Michael respectively. (-10 means he has sold 10 shares, +10 means he has bought 10 shares)

there are 10 different possible cases according to the initial and final share price.

Please note that Chetan will always be having -10 shares(10 shares sold) and 1300 as cash.

This is because Chetan buys for every fall in price and sells for every rise in price. But the fluctuation in share price is constant as it starts from 100 and closes at 110 on day 5. So, in total Chetan will always sell 10 shares in all 5 days combined.

As Chetan has sold 10 shares, he’ll get 110*10 =1100 cash because of it in every case. Also, Chetan earns Rs. 200 in every case because of buying at low and selling at high. So total cash Chetan will always have after 5 days = 1100+200 =1300.

The question asks about the case where there has been the maximum possible increase in the combined cash balance of Chetan and Michael at the end of the fifth day.

As we know chetan has 1300 cash in all the cases , so we have to maximize the case where Michael has the most cash.

Also, if we see clearly, the profit made by selling and buying is in hundreds while the cash received by selling the shares is much far in terms of cash.
As 10 shares sold give = 10*110 = 1100 cash. So we have to look at the case where Michael has sold most shares which is case 8.

In case 8 the price rises from 100 to 110 ->120 ->130 ->120 ->110

in this case 110(0 new shares)->120(Michael sold 10 shares)->130(Michael sold 10 shares)120(Michael sold 10 shares)->110(Michael does nothing) = 30 shares sold in total

Cash =  20 shares at 120 and 10 shares at 130 =  120*20+130*10 = 2400+1300 =3700

As Chetan has 1300 cash and Michael has 3700 cash;
total cash they have is : 3700+1300 =5000

Question 24: If Michael ended up with 20 more shares than Chetan at the end of day 5, what was the price of the share at the end of day 3?

a) Rs 90

b) Rs 100

c) Rs 110

d) Rs 120

e) Rs 130

24) Answer (A)

View Video Solution

Solution:

The above table includes the values of the share price at the end of each day. Chetan and Michael column shows the number of shares at the end of 5th day with Chetan and Michael respectively. (-10 means he has sold 10 shares, +10 means he has bought 10 shares)

there are 10 different possible cases according to the initial and final share price.

Please note that Chetan will always be having -10 shares(10 shares sold) and 1300 as cash.

To have 20 more shares than Chetan, Michael has to buy 10 shares which is case 1.

In case 1, the share price at the end of day 3 is 90.

Download CAT Maths formulas PDF

Instructions

Answer the following questions based on the information given below:

In a sports event, six teams (A, B, C, D, E and F) are competing against each other Matches are scheduled in two stages. Each team plays three matches in Stage – I and two matches in Stage – II. No team plays against the same team more than once in the event. No ties are permitted in any of the matches. The observations after the completion of Stage – I and Stage – II are as given below.

Stage-I:

• One team won all the three matches.

• Two teams lost all the matches.

• D lost to A but won against C and F.

• E lost to B but won against C and F.

• B lost at least one match.

• F did not play against the top team of Stage-I.

Stage-II:

• The leader of Stage-I lost the next two matches

• Of the two teams at the bottom after Stage-I, one team won both matches, while the other lost both matches.

• One more team lost both matches in Stage-II.

Question 25: The two teams that defeated the leader of Stage-I are:

a) B & F

b) E & F

c) B & D

d) E & D

e) F & D

25) Answer (B)

View Video Solution

Solution:

There are a total of $^6 C_2$ matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.

From the information given, we can conclude that the following matches were held in first stage:

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)

One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.

From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).

Thus, the stage 1 matches are

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)

Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)

As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:

Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)

Hence, the two teams that won against stage 1 leader A are E and F.

Question 26: The only team(s) that won both matches in Stage-II is (are):

a) B

b) E & F

c) A, E & F

d) B, E & F

e) B & F

26) Answer (D)

View Video Solution

Solution:

There are a total of $^6 C_2$ matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.

From the information given, we can conclude that the following matches were held in first stage:

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)

One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.

From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).

Thus, the stage 1 matches are

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)

Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)

As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:

Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)

Hence, the teams that won both of their stage 2 matches are B, E and F.

Question 27: The teams that won exactly two matches in the event are:

a) A, D & F

b) D & E

c) E & F

d) D, E & F

e) D & F

27) Answer (E)

View Video Solution

Solution:

There are a total of $^6 C_2$ matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.

From the information given, we can conclude that the following matches were held in first stage:

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)

One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.

From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).

Thus, the stage 1 matches are

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)

Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)

As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:

Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)

Hence, the wins by each team are A (3), B(4), C(0), D(2), E(4), F(2). Hence, D and F won exactly 2 matches.

Question 28: The team(s) with the most wins in the event is (are):

a) A

b) A & C

c) F

d) E

e) B & E

28) Answer (E)

View Video Solution

Solution:

There are a total of $^6 C_2$ matches => 15 matches. The first 9 matches are held in the first stage and remaining 6 in the second stage.

From the information given, we can conclude that the following matches were held in first stage:

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won)

One team won all matches. As B, C, D E and F have lost at least one match each, A won all three matches. As A, B, D, E have won at least one match, C and F lost both matches.

From the matches already deduced, we can see that A needs to play 2 more matches, B two more matches and C and F one match each. As C and F lose all matches in stage 1, they cannot play against each other. F did not play against the leader i.e. A. Hence, the remaining matches are A-B (A won), A-C (A won), B-F (B won).

Thus, the stage 1 matches are

Stage 1: D-A (A won), D-C (D won), D-F (D won), E-B (B won), E-C (E won), E-F (E won), A-B (A won), A-C (A won), B-F (B won)

Thus Stage 2 matches are D-B, D-E, E-A, F-A, B-C and C-F (all matches – stage 1 matches)

As A lost both matches, F and E must have won the match vs A. As F won against A, F won both its matches and C lost both its matches. One more team lost both its matches. As B, E and F have won at least one match and A and C have been discussed previously, D must have lost both matches. Hence, stage 2 results are:

Stage 2: D-B (B won), D-E (E won), E-A (E won), F-A (F won), B-C (B won) and C-F (F won)

Hence, the wins by each team are A(3), B(4), C(0), D(2), E(4), F(2). Hence, most wins are by B and E.

Enroll to CAT 2022 Complete Course

Instructions

In the table below is the listing of players, seeded from highest (#1) to lowest (#32), who are due to play in an Association of Tennis Players (ATP) tournament for women. This tournament has four knockout rounds before the final, i.e., first round, second round, quarterfinals, and semi-finals. In the first round, the highest seeded player plays the lowest seeded player (seed # 32) which is designated match No. 1 of first round; the 2nd seeded player plays the 31st seeded player which is designated match No. 2 of the first round, and so on. Thus, for instance, match No. 16 of first round is to be played between 16th seeded player and the 17th seeded player. In the second round, the winner of match No. 1 of first round plays the winner of match No. 16 of first round and is designated match No. 1 of second round. Similarly, the winner of match No. 2 of first round plays the winner of match No. 15 of first round, and is designated match No. 2 of second round. Thus, for instance, match No. 8 of the second round is to be played between the winner of match No. 8 of first round and the winner of match No. 9 of first round. The same pattern is followed for later rounds as well.

<img “=”” alt=”” class=”img-responsive” src=”https://cracku.in/media/questionGroup/DI_4_5.png”/>

Question 29: If there are no upsets (a lower seeded player beating a higher seeded player) in the first round, and only match Nos. 6, 7, and 8 of the second round result in upsets, then who would meet Lindsay Davenport in quarter finals, in case Davenport reaches quarter finals?

a) Justine Henin

b) Nadia Petrova

c) Patty Schnyder

d) Venus Williams

29) Answer (D)

View Video Solution

Solution:

There are no upsets in 1st round, so top 16 players go to the 2nd round.

In second round, nth player would play (17-n)th player. Now, match Nos. 6, 7, and 8 of the second round result in upsets.

So the people in the quarter finals would be 1,2,3,4,5,11,10,9.

So in quarterfinal 2nd seeeded player would play (9-2) = 7th position player.

Here no. 10 is in the 7th position and No. 10 player is venus williams.

Hence option D.

Question 30: If Elena Dementieva and Serena Williams lose in the second round, while Justine Henin and Nadia Petrova make it to the semi-finals, then who would play Maria Sharapova in the quarterfinals, in the event Sharapova reaches quarterfinals?

a) Dinara Safina

b) Justine Henin

c) Nadia Petrova

d) Patty Schnyder

30) Answer (C)

View Video Solution

Solution:

If Elena Dementieva and Serena Williams lose in the second round, Nadia petrova  and patty schnyder will go through.

Hence ,in the quarter finals, following seed no. players will be in  quarter finals: 1,2,3,4,5,11,7,9.

So, now Maria Sharapova is ranked is 1 so she’ll play 9th seed player who is Nadia Petrova.

Hence option C.

Question 31: If, in the first round, all even numbered matches (and none of the odd numbered ones) result in upsets, and there are no upsets in the second round, then who could be the lowest seeded player facing Maria Sharapova in semi-finals?

a) Anastasia Myskina

b) Flavia Pennetta

c) Nadia Petrova

d) Svetlana Kuznetsova

31) Answer (A)

View Video Solution

Solution:

According to given condition, players of following ranking will go to the 2nd round 1,31,3,29,5,27,7,25,9,23,11,21,13,19,15,17.

Out of these players going to 3rd round / quarter finals are 1,15,3,13,5,11,7,9.

If maria (no.1) goes to semifinal she’ll face any on eout of the 13/5 th no. player in semis.

13th seed player is the lowest so Anastasia Myskina.

Question 32: If the top eight seeds make it to the quarterfinals, then who, amongst the players listed below, would definitely not play against Maria Sharapova in the final, in case Sharapova reaches the final?

a) Amelie Mauresmo

b) Elena Dementieva

c) Kim Clijsters

d) Lindsay Davenport

32) Answer (C)

View Video Solution

Solution:

If the top eight seeds make it to the quarterfinals then one out of Kim Clijsters or svetana kuznetsova will compete with maria sharapoava in semis.

So now if maria reaches semis, she’ll beat any one out of the two and both will definitely not play against Maria Sharapova in the final, if she reaches.

Download CAT Previous Papers PDF (1990-2021)

Instructions

The following questions relate to a game to be played by you and your friend. The game consists of a 4 x 4 board (see below) where each cell contains a positive integer. You and your friend make moves alternately. A move by any of the players consists of splitting the current board configuration into two equal halves and retaining one of them. In your moves you are allowed to split the board only vertically and to decide to retain either the left or the right half. Your friend, in his/her moves, can split the board only horizontally and can retain either the lower or the upper half. After two moves by each player a single cell will remain which can no longer be split and the number in that cell will be treated as the gain (in rupees) of the person who has started the game. A sample game is shown below. So your gain is Re.1. With the same initial board configuration as above and assuming that you have to make the first move, answer the following questions.
Initial Board

After your move (retain left)

After your friends move (retain upper)

After your move (retain right)

After your friends move (retain lower)

Question 33: If you choose (retain right) (retain left) in your turns, the best move sequence for your friend to reduce your gain to a minimum will be

a) (retain upper)(retain lower)

b) (retain lower) (retain upper)

c) (retain upper) (retain upper)

d) (retain lower) (retain lower)

33) Answer (C)

View Video Solution

Solution:

After my first move of retaining right board will be like

Now second person will force me to retain with the lowest value possible i.e. 2 or 3
So if he retains lower half and i retain with left one (as mentioned) then he can only force me to pick 3.
Or if he retains upper half and i retain with left one(as mentioned) then he can retain upper half so i will be having minimized profit of 2.
Hence second person will have moves as “Retain (upper half) and retain (upper half)”

Question 34: If both of you select your moves intelligently then at the end of the game your gain will be

a) Rs.4

b) Rs.3

c) Rs.2

d) None of these

34) Answer (B)

View Video Solution

Solution:

After second move i will be having from a quarter cell of board to make a move.

Since left quarters have cells with values 1, Hence i will choose to retain right in my first move so that second person can force my profit to be either 2 or 3 not 1.

So now after my first move of retaining right, we have two quarters

Now intelligently he will make a move to retain with lower half so that at fourth move i can retain with choices of 2 and 3 not 2 and 4.

Question 35: If your first move is (retain right), then whatever moves your friend may select you can always force a gain of no less than

a) Rs.3

b) Rs.6

c) Rs.4

d) None of these

35) Answer (A)

View Video Solution

Solution:

After retaining right in first move, second person will have 2 quarters to choose in which minimum value is 2 and 3.
If he retains upper half, i will retain right as to maximize my profit of either 4 or 7.
If he retains lower half, i will retain left as to maximize my profit of either 3 or 8.
Hence whatever he retains, i won’t have a profit less than 3.

Instructions

Ten players, as listed in the table below, participated in a rifle shooting competition comprising of 10 rounds. Each round had 6 participants. Players numbered 1 through 6 participated in Round 1, players 2 through 7 in Round 2,…, players 5 through 10 in Round 5, players 6 through 10 and 1 in Round 6, players 7 through 10, 1 and 2 in Round 7 and so on. The top three performances in each round were awarded 7, 3 and 1 points respectively. There were no ties in any of the 10 rounds. The table below gives the total number of points obtained by the 10 players after Round 6 and Round 10.

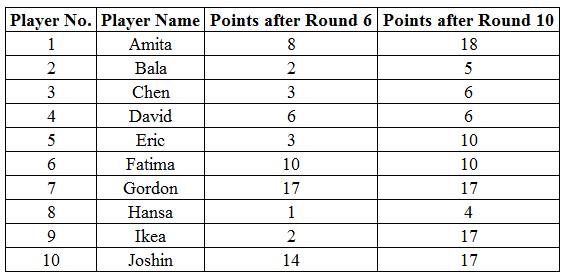
The following information is known about Rounds 1 through 6:
1. Gordon did not score consecutively in any two rounds.
2. Eric and Fatima both scored in a round.
The following information is known about Rounds 7 through 10:
1. Only two players scored in three consecutive rounds. One of them was Chen. No other player scored in any two consecutive rounds.
2. Joshin scored in Round 7, while Amita scored in Round 10.
3. No player scored in all the four rounds.

Question 36: What were the scores of Chen, David, and Eric respectively after Round 3?

a) 3, 6, 3

b) 3, 3, 3

c) 3, 3, 0

d) 3, 0, 3

36) Answer (B)

View Video Solution

Solution:

From the condition given in the premise, we can make the following table:

The information known about Rounds 1 through 6:
1. Gordon(G) did not score consecutively in any two rounds.
2. Eric(E) and Fatima(F) both scored in a round.

By observing the table:

1. Jordan(J) scored 7 points in both the rounds 5th & 6th.

2. Amita (A) scored 1,7 points then she scored 7 in the first round.

3. Bala (B) scored 1 point in both the rounds 1st and 2nd.

4. Ikea (I) scored 1 point in the round 4th and 5th.

5. Gordon(G- 7,7,3 ) did not score consecutively in any two rounds so it scored in 2^nd, 4^th and 6^th rounds respectively.

We can make the following table from the details given in the question.

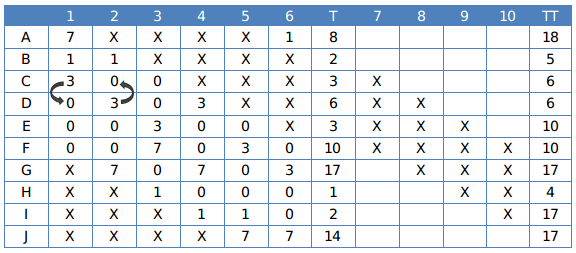
T: Total after the sixth round and TT: Total after the 10th round.

1. Only two players scored in three consecutive rounds. One of them was Chen. So He scored 1 point in the rounds 8th, 9th and 10th.

2. Ikea scored 15 points (1,7,7) in three rounds respectively.

3. Eric scored 7 in round 10.

4. Amita will score 3 in round 10, and 7 in round 7.

We can make the following table:

Hence option B is correct.

Question 37: Which three players were in the last three positions after Round 4?

a) Bala, Ikea, Joshin

b) Bala, Hansa, Ikea

c) Bala, Chen, Gordon

d) Hansa, Ikea, Joshin

37) Answer (D)

View Video Solution

Solution:

From the condition given in the premise, we can make the following table:

The information known about Rounds 1 through 6:
1. Gordon(G) did not score consecutively in any two rounds.
2. Eric(E) and Fatima(F) both scored in a round.

By observing the table:

1. Jordan(J) scored 7 points in both the rounds 5th & 6th.

2. Amita (A) scored 1,7 points then she scored 7 in the first round.

3. Bala (B) scored 1 point in both the rounds 1st and 2nd.

4. Ikea (I) scored 1 point in the round 4th and 5th.

5. Gordon(G- 7,7,3 ) did not score consecutively in any two rounds so it scored in 2^nd, 4^th and 6^th rounds respectively.

We can make the following table from the details given in the question.

T: Total after the sixth round and TT: Total after the 10th round.

1. Only two players scored in three consecutive rounds. One of them was Chen. So He scored 1 point in the rounds 8th, 9th and 10th.

2. Ikea scored 15 points (1,7,7) in three rounds respectively.

3. Eric scored 7 in round 10.

4. Amita will score 3 in round 10, and 7 in round 7.

We can make the following table:

Hence option D is correct.

Question 38: Which player scored points in maximum number of rounds?

a) Joshin

b) Chen

c) Amita

d) Ikea

38) Answer (D)

View Video Solution

Solution:

From the condition given in the premise, we can make the following table:

The information known about Rounds 1 through 6:
1. Gordon(G) did not score consecutively in any two rounds.
2. Eric(E) and Fatima(F) both scored in a round.

By observing the table:

1. Jordan(J) scored 7 points in both the rounds 5th & 6th.

2. Amita (A) scored 1,7 points then she scored 7 in the first round.

3. Bala (B) scored 1 point in both the rounds 1st and 2nd.

4. Ikea (I) scored 1 point in the round 4th and 5th.

5. Gordon(G- 7,7,3 ) did not score consecutively in any two rounds so it scored in 2^nd, 4^th and 6^th rounds respectively.

We can make the following table from the details given in the question.

T: Total after the sixth round and TT: Total after the 10th round.

1. Only two players scored in three consecutive rounds. One of them was Chen. So He scored 1 point in the rounds 8th, 9th and 10th.

2. Ikea scored 15 points (1,7,7) in three rounds respectively.

3. Eric scored 7 in round 10.

4. Amita will score 3 in round 10, and 7 in round 7.

We can make the following table:

Hence option D is correct.

Question 39: Which players scored points in the last round?

a) Amita, Eric, Joshin

b) Amita, Chen, David

c) Amita, Bala, Chen

d) Amita, Chen, Eric

39) Answer (D)

View Video Solution

Solution:

From the condition given in the premise, we can make the following table:

The information known about Rounds 1 through 6:
1. Gordon(G) did not score consecutively in any two rounds.
2. Eric(E) and Fatima(F) both scored in a round.

By observing the table:

1. Jordan(J) scored 7 points in both the rounds 5th & 6th.

2. Amita (A) scored 1,7 points then she scored 7 in the first round.

3. Bala (B) scored 1 point in both the rounds 1st and 2nd.

4. Ikea (I) scored 1 point in the round 4th and 5th.

5. Gordon(G- 7,7,3 ) did not score consecutively in any two rounds so it scored in 2^nd, 4^th and 6^th rounds respectively.

We can make the following table from the details given in the question.

T: Total after the sixth round and  TT: Total after the 10th round.

1. Only two players scored in three consecutive rounds. One of them was Chen. So He scored 1 point in the rounds 8th, 9th and 10th.

2. Ikea scored 15 points (1,7,7) in three rounds respectively.

3. Eric scored 7 in round 10.

4. Amita will score 3 in round 10, and 7 in round 7.

We can make the following table:

Hence option D is correct.

Take 3 Free CAT Mocks Here

Instructions

The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each. Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:

1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.

Question 40: What were the bids by Arun, Bankim, Charu and Dipak, respectively in the first round?

a) Hi, Lo, Lo, Hi

b) Hi, Lo, Lo, Lo

c) Hi, Hi, Lo, Lo

d) Lo, Lo, Lo, Hi

40) Answer (A)

View Video Solution

Solution:

Let ‘H’ represents Hi and ‘L’ represents Lo.

Given if they bid

Case 1: HHHH then all players gets -1 points.

Case 2: HHHL => H gets +1 and L gets -3.

Case 3: HHLL => H gets +2 and L gets -2.

Case 4: HLLL => H gets +3 and L gets -1.

Case 5: LLLL => every player gets +1.

From the given information we can draw the following table:

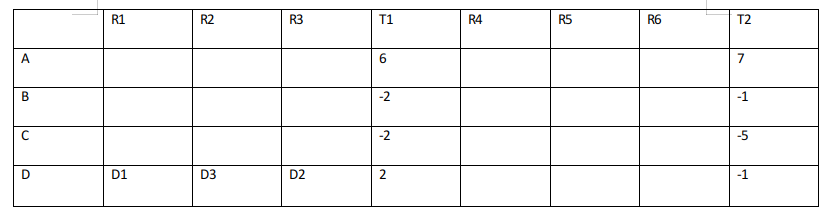
**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.

**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.

From point 3, D1>D2>D3

D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :

Case D1: 3,2,-3

In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.

Case D2: 2,1,-1

In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.

Case D3: 3,1,-2

In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.

.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.

Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.

Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.

Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.

With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.

Given In exactly two out of the six rounds, Arun was the only player who bid Hi.

Let R.x, R.y, R.z represent R4, R5, R6 in any order.

Let A bid H in R.x=> B,C,D bid L.

The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2

For B, R.x+R.y+R.z=1 => R.y+R.z=2

For C, R.x+R.y+R.z=-3 => R.y+R.z=-2

For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2

(R.y, R.z) for A can be (-3,1) or (-1,-1)

Case A1:

If for A, (R.y, R.z)=(-3,1)

Since for both C,D: R.y+R.z=-2

We can’t get any combination such that the total points of B,C,D are obtained.

Case A2:

If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1), (-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively while A must have bid (L, H)

Hence this case is valid.

The final table looks like:

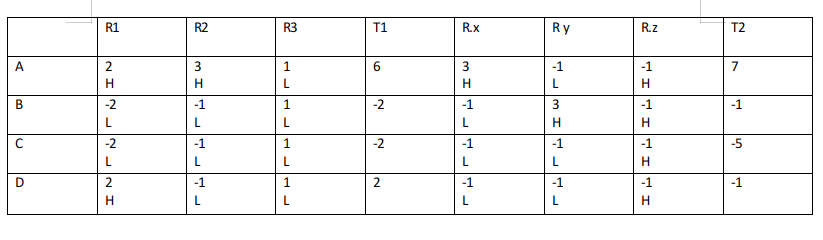
The bids by Arun, Bankim, Charu and Dipak, respectively in the first round are HLLH.

Hence Option A is correct.

Question 41: In how many rounds did Arun bid Hi?

Question 42: In how many rounds did Bankim bid Lo?

Question 43: In how many rounds did all four players make identical bids?

Question 44: In how many rounds did Dipak gain exactly 1 point?

Question 45: In which of the following rounds, was Arun DEFINITELY the only player to bid Hi?

a) Second

b) Third

c) Fourth

d) First

45) Answer (A)

View Video Solution

Solution:

Let ‘H’ represents Hi and ‘L’ represents Lo.

Given if they bid

Case 1: HHHH then all players gets -1 points.

Case 2: HHHL => H gets +1 and L gets -3.

Case 3: HHLL => H gets +2 and L gets -2.

Case 4: HLLL => H gets +3 and L gets -1.

Case 5: LLLL => every player gets +1.

From the given information we can draw the following table:

**T1 is the cumulative of points till Round 3 and T2 is sum of points till round 6.

**Arun, Bankim, Charu, and Dipak are represented by A, B, C, D respectively.

From point 3, D1>D2>D3

D scored 2 points till round R3 and D1>D3>D2 the possible scenarios are :

Case D1: 3,2,-3

In this case the points of A in R1, R3, R2 will be -1,2/-2, 1 in any
possible combination the sum will not be 6. So, this case is invalid.

Case D2: 2,1,-1

In this case the points of A in R1, R3, R2 will be 2/-2, 1/-3, -1/3
so, if the points in R1, R3, R2 are 2,1,3 the case is valid and no other
cases are possible.

Case D3: 3,1,-2

In this case the points of A in R1, R3, R2 will be -1, 1/-3/1, 2/-2
in any possible combination the sum will not be 6. So, this case is
invalid.

.’. Points of A,D in (R1,R2,R3) are (2,3,1) and (2,-1,1) respectively.

Since A got +3 in R2, he is only the one to bid h in R2 and points of B and C in round 2 are -1,-1 i.e they bid L, L.

Since A and D got 2 points each in R1, C and B must have got -2, -2 i.e they bid L, L.

Since A and D got 1 point in R3, C and B must also have got 1 in R3 i.e they bid L, L.

With this data, the table now looks like:

No information is given about the individual scores in R4, R5, R6.

Given In exactly two out of the six rounds, Arun was the only player who bid Hi.

Let R.x, R.y, R.z represent R4, R5, R6 in any order.

Let A bid H in R.x=> B,C,D bid L.

The table now looks like:

For A, R.x+R.y+R.z=1 => R.y+R.z=-2

For B, R.x+R.y+R.z=1 => R.y+R.z=2

For C, R.x+R.y+R.z=-3 => R.y+R.z=-2

For D, R.x+R.y+R.z=-3.=> R.y+R.z=-2

(R.y, R.z) for A can be (-3,1) or (-1,-1)

Case A1:

If for A, (R.y, R.z)=(-3,1)

Since for both C,D: R.y+R.z=-2

We can’t get any combination such that the total points of B,C,D are obtained.

Case A2:

If for A, (R.y, R.z)=(-1,-1).the (R.y, R.z) of B,C,D can be (3,-1),
(-1,-1), (-1,-1) and they must have bid (H,H), (L,H), (L,H) respectively
while A must have bid (L, H)

Hence this case is valid.

The final table looks like:

R2 is correct answer.

Top DILR Sets | LRDI Preparation Videos