Time, Speed and Distance Questions for NMAT

Time, Speed and Distance Questions for NMAT:

Download Time, Speed and Distance Questions for NMAT PDF. Top 10 very important Time, Speed and Distance Questions for NMAT based on asked questions in previous exam papers.

Download Time, Speed and Distance Questions for NMAT

Get 5 NMAT Mocks for Rs. 499

Take NMAT mock test

Question 1: Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is

a) 5

b) 3

c) 2

d) 4

Question 2: The distance from B to C is thrice that from A to B. Two trains travel from A to C via B. The speed of train 2 is double that of train 1 while traveling from A to B and their speeds are interchanged while traveling from B to C. The ratio of the time taken by train 1 to that taken by train 2 in travelling from A to C is

a) 5:7

b) 4:1

c) 1:4

d) 7:5

Question 3: One can use three different transports which move at 10, 20, and 30 kmph, respectively to reach from A to B. Amal took each mode of transport for $\frac{1}{3}^{rd}$ of his total journey time, while Bimal took each mode of transport for $\frac{1}{3}^{rd}$ of the total distance. The percentage by which Bimal’s travel time exceeds Amal’s travel time is nearest to

a) 22

b) 20

c) 19

d) 21

Question 4: A man and a woman 81 miles apart from each other, start travelling towards each other at the same time. If the man covers 5 miles per hour to the women’s 4 mile per hour, how far will the woman have travelled when they meet?

a) 27

b) 36

c) 45

d) None of these

Question 5: A train starts from Delhi at 6 : 00 AM and reaches Ambala Cantt at 10 AM. The other train starts from Ambala Cantt at 8 AM and reaches Delhi at 11:30 AM. If the distance between Delhi and Ambala Cantt. is 200 km, then at what time did the two trains meet each other ?

a) 8 : 56 AM

b) 8 : 46 AM

c) 7 : 56 AM

d) 8 : 30 AM

Question 6: A man leaves his home and walks at a speed of 12 km per hour, reaching the railway station 10 minutes after the train had departed. If instead he had walked at a speed of 15 km per hour, he would have reached the station 10 minutes before the train’s departure. The distance (in km) from his home to the railway station is

Question 7: Prasoon has to travel from Hyderabad to Bangalore and return back to Hyderabad. He traveled $\frac{2}{5}^{th}$ of his journey towards Bangalore with the speed of 60 km/kr and the remaining distance was covered in 80km/hr. While returning back he traveled back in a speed such that the time taken to travel from Hyderabad to Bangalore is the same as the time taken to travel from Bangalore to Hyderabad. What is his average return speed?

a) 64.57 km/hr

b) 65.75 km/hr

c) 70.58 km/r

d) 74.31 km/hr

Question 8: Leaving home at the same time, Amal reaches the office at 10:15 am if he travels at 8 km/hr, and at 9:40 am if he travels at 15 km/hr. Leaving home at 9.10 am, at what speed, in km/hr, must he travel so as to reach office exactly at 10 am?

a) 13

b) 12

c) 14

d) 11

Question 9: A 150 m long train is approaching a crossing that is 1.5 km away at 108 kmph. Another train, 200 m long and moving at 72 kmph, is 1 km from the crossing. In the meantime, a bike that is 600 m away approaches the crossing on the road perpendicular to it. If S is the speed of the bike (in m/s), which of the following options correctly represents the values that S can take such that the bike avoids a collision with the trains?

a)  $ S \geq 12 $ or $ S \leq \frac{200}{19}$

b)  $ S \geq 12 $ or $ S \leq 10$

c)  $ S \geq 11 $ or $ S \leq \frac{120}{11}$

d)  $ S \geq 11 $ or $ S \leq 9$

Question 10: A boat takes 1 hour less to travel 120km downstream
than to travel the same distance upstream. If the speed of the
stream is 10km/hr, then find the speed of the boat?

Join 7K MBA Aspirants Telegram Group

Download Highly Rated CAT preparation App

Answers & Solutions:

1) Answer (B)

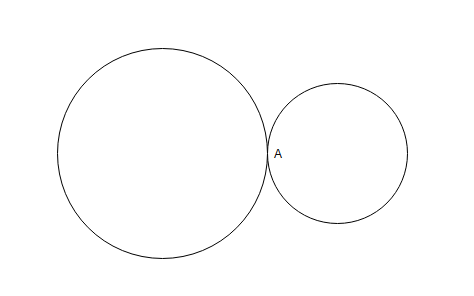
To complete one round Ram takes 100m/15kmph and Rahim takes 20m/5kmph

They meet for the first time after L.C.M of (100m/15kmph , 20m/5kmph) = 100m/5kmph=20m/kmph.

Distance traveled by Ram =20m/kmph * 15kmph =300m.

So, he must have ran 300/100=3 rounds.

Note:

CAT gave both 2 and 3 as correct answers because of the word ‘before‘.

2) Answer (A)

Let the distance from A to B be “x”, then the distance from B to C will be 3x. Now the speed of Train 2 is double of Train 1. Let the speed of Train 1 be “v”, then the speed of Train 2 will be “2v” while travelling from A to B.

Time taken by Train 1 = (x/v)

Time taken by Train 2 = (x/2v)

Now from B to C distance is “3x” and the speed of Train 2 is (v) and the speed of Train 1 is (2v).

Time taken by Train 1 = 3x/2v

Time taken by Train 2 = 3x/v

Total time taken by Train 1 = x/v(1+(3/2)) = (5/2)(x/v)

Total time taken by Train 2 = x/v(3+(1/2))= (7/2)(x/v)

Ratio of time taken = $\frac{5}{\frac{2}{\frac{7}{2}}}=\frac{5}{7}$

3) Answer (A)

Assume the total distance between A and B as d and time taken by Amal = t

Since Amal travelled $\frac{1}{3}^{rd}$ of his total journey time in different speeds
d = $\ \frac{\ t}{3}\times\ 10+\ \frac{\ t}{3}\times\ 20+\frac{\ t}{3}\times\ 30\ \ =\ 20t$

$\text{Total time taken by Bimal} = \ \frac{d_1}{s_1}+\frac{d_2}{s_2}+\frac{d_3}{s_3}$

$=\ \frac{20t}{3}\times\ \frac{1}{10}+\frac{20t}{3}\times\ \frac{1}{20}+\frac{20t}{3}\times\ \frac{1}{30}\ \ =\frac{20t\left(6+3+2\right)}{3\ \times30}\ =\frac{11}{9}t$

Hence, the ratio of time taken by Bimal to time taken by Amal = $\frac{\frac{11t}{9}}{t}=\frac{11}{9}$
Therefore, Bimal will exceed Amal’s time by $\ \ \ \frac{\ \ \frac{\ 11t}{9}-t}{t}\times\ 100 = 22.22%$

4) Answer (B)

Time taken to meet = $\ \frac{\ Dis\tan ce\ between\ them\ }{Relative\ speed}$

Relative Speed = 5 +4 = 9 miles per hour.
Time take to cover 81 miles = $\ \frac{\ 81\ }{9}$ = 9 hours.
Woman travelled in 9 hours = 9*4 = 36 miles.

5) Answer (A)

Let t be the start time

A starts at t, while B starts at (t-2)

Total distance covered = 200 km

As they are travelling in the opposite direction,

Relative distance covered i,e 200=((200/4)*t )+((400/7)*(t-2))

t=176min i.e 2hrs 56min from start (6 am)

Therefore they meet at 8.56 am.

A is the correct answer.

6) Answer: 20

We see that the man saves 20 minutes by changing his speed from 12 Km/hr to 15 Km/hr.

Let d be the distance

Hence,

$\frac{d}{12} – \frac{d}{15} = \frac{1}{3}$

$\frac{d}{60} = \frac{1}{3}$

d = 20 Km.

7) Answer (C)

Let the distance between Hyderabad and Bangalore be $x$. and return speed be $y$km/hr

Distance covered with speed of 60km/hr = $\frac{2x}{5}$. Time taken = $\frac{2x}{5\left(60\right)}=\frac{x}{150}$

Distance covered with speed of 80km/hr = $\frac{3x}{5}$. Time taken = $\frac{3x}{5\left(80\right)}=\frac{3x}{400}$

The time taken for return journey = $\frac{x}{y}$

Upon equating time, we get

$\frac{x}{150}+\frac{3x}{400}=\frac{x}{y}$

$\frac{8x}{1200}+\frac{9x}{1200}=\frac{x}{y}$

$\frac{17x}{1200}=\frac{x}{y}$ or $y=\frac{1200}{7}=70.58\ \frac{km}{hr}$

8) Answer (B)

The difference in the time take to traverse the same distance $’d’$ at two different speeds is 35 minutes. Equating this: $\frac{d}{8}-\frac{d}{15}\ =\ \frac{35}{60}$

On solving, we obtain $d = 10 kms$. Let $x kmph$ be the speed at which Amal needs to travel to reach the office in 50 minutes; then

$\frac{10}{x}=\frac{50}{60}\ or\ x\ =\ 12\ kmph$.Hence, Option B is the correct answer.

9) Answer (B)

The speed of the trains in m/s: $T_1$ = 30 m/s and $T_2$=20 m/s respectively.

An initial representation of the positions of the trains and the bike is shown below:

Time taken by the Train T1 to reach the junction = 1500/30 = 50 seconds

Time taken by the Train T1 to completely cross the junction = (1500+150)/30 = 55 seconds

Time taken by the Train T2 to reach the junction = 1000/20 = 50 seconds

Time takne by the Train T2 to completely cross the junction = (1000 + 200)/20 = 60 seconds.

Hence the bike should not cross the junction between 50 seconds and 60 seconds.

=> 50  $\leq$ Time taken by the bike to reach the junction $\leq$ 60

=> $ S \geq 600/50 $ or  $ S \leq 600/ 60$

=> $ S \geq 12 $ or $ S \leq 10$

10) Answer: 50

Assume the speed of
boat with respect to
water = v

Then, 120/(v-10) –
120/(v+10) = 1

=> v^2-100 = 2400

=> v=50 km/hr

Get 5 NMAT Mocks for Rs. 499

We hope this Time, Speed and Distance Questions for NMAT pdf for NMAT exam will be highly useful for your Preparation.