SSC GD Constable Maths Question Paper PDF
SSC GD Constable maths previous year Question paper download PDF based on last years SSC exams. 40 Very important mathematics previous questions for GD Constable.
DOWNLOAD SSC GD Reasoning Previous Papers PDF
GET 20 SSC GD MOCK FOR JUST RS. 117
Question 1: A 270 meters long train running at the speed of 120 kmph crosses another train running in opposite direction at the speed of 80 kmph in 9 seconds. What is the length of the other train ?
a) 240 meters
b) 320 meters
c) 260 meters
d) 230 meters
Question 2: Raviraj invested an amount of Rs.10,000 at compound interest rate of 10 p.e.p.a. For a period of three years. How much amount will Raviraj et after three years ?
a) Rs.13,210
b) Rs.13,310
c) Rs.12,100
d) Rs.11,000
Question 3: Twice the square of a number is the cube of 18. The number is
a) 54
b) 108
c) 162
d) 324
Question 4: The average salary of a group of 27 is Rs. 3,700. If the salary of one more person is added, the average is increased to Rs.3750. What is the salary of the new person ?
a) Rs.5010
b) Rs.5200
c) Rs.5100
d) Rs.5000
Question 5: What should come in place of both the question marks (?) in the following equation. $\frac{16}{?}=\frac{?}{42.25}$
a) 2.6
b) 260
c) .26
d) 26
Download SSC GD FREE PREVIOUS PAPERS
Question 6: An amount of money is to be distributed among P, Q and R in the ratio of 5:9:17 respectively. If the total of the shares of P and Q is Rs.7,000. What is R’s share in it
a) Rs.4,500
b) Rs.2,500
c) Rs.8,500
d) Rs.6,000
Question 7: One-fourth of three-fifth of a number is 42. What is 40% of that number ?
a) 140
b) 116
c) 128
d) 112
Question 8: By how much is 10% of 24.2 more than 10% of 24.02 ?
a) 1.8
b) 0.018
c) 0.18
d) 18
Question 9: Ramesh bought a calculator with 20% discount on the tag price. He obtained 10% profit by selling it for Rs.440. What was the tag price ?
a) Rs.500
b) Rs.400
c) Rs.480
d) Rs.360
Question 10: The sum of two numbers is 22 and their difference is 14. Find the product of numbers.
a) 72
b) 82
c) 62
d) 27
DOWNLOAD APP TO ACESS DIRECTLY ON MOBILE
Question 11: If m = 9 and n = $\frac{1}{3}\ $m, then $\ \sqrt{(m)^{2}-(n)^{2}=?}$
a) $2\sqrt2$
b) $6\sqrt2$
c) $4\sqrt2$
d) $5\sqrt2$
Question 12: The ratio between the ages of x and y at present is 3:4. Five years hence, the ratio of their ages will be 4:5; what is the present age of y in years ?
a) 15
b) 20
c) 25
d) 30
Question 13: What would come in place of (\$) mark in the following equation ?
* 2 $ 20 ÷ 156 = 145
a) 6
b) 2
c) 4
d) 0
Question 14: $2\frac{1}{5}x^{2}\ $= 2750, find the value of x ?
a) 25
b) $25\sqrt{3}$
c) $25\sqrt{2}$
d) 20
Question 15: $\frac{75\times75-26\times26}{101}=?$
a) 59
b) 39
c) 29
d) 49
FREE SSC PRACTICE SET (DAILY TEST)
Question 16: $\angle ABC\ $is an isosceles triangle and $\ \overline{AB}\ $=$ \overline{AC}\ $= 2a unit $\ \overline{BC}\ $= a unit, Draw $ \overline{AD}\ \bot\ \overline{BC},\ $and find the length of $\ \overline{AD}$
a) $\sqrt{15}\ $a unit
b) $\frac{\sqrt{15}}{2}\ $a unit
c) $\sqrt{17}\ $a unit
d) $\frac{\sqrt{17}}{2}\ $a unit
Question 17: All sides of a quadrilateral ABCD touch a circle. If AB = 6 cm. BC = 7.5 cm. CD = 3 cm, then DA is
a) 3.5 cm
b) 4.5 cm
c) 2.5 cm
d) 1.5 cm
Question 18: In a right angled triangle, the product of two sides is equal to half of the square of the third side i.e., hypotenuse. One of the acute angles must be
a) $60^\circ$
b) $30^\circ$
c) $45^\circ$
d) $15^\circ$
Question 19: If two concentric circles are of radii 5 cm and 3 cm, then the length of the chord of the larger circle which touches the smaller circle is
a) 6 cm
b) 7 cm
c) 10 cm
d) 8 cm
Question 20: Inside a square ABCD, $\ \triangle BEC\ $is an equilateral triangle. If CE and BD interesect at O, then $\ \angle BOC\ $ is equal to
a) $60^\circ$
b) $75^\circ$
c) $90^\circ$
d) $120^\circ$
Question 21: A point D is taken from the side BC of a right angled triangle ABC, where AB is hypotenuse. Then,
a) $AB^{2}+CD^{2}=BC^{2}+AD^{2}$
b) $CD^{2}+BD^{2}=2AD^{2}$
c) $AB^{2}+AC^{2}=2AD^{2}$
d) $AB^{2}+AD^{2}=BD^{2}$
Question 22: Let C be a point on a straight line AB. Circles are drawn with diameters AC and AB. Let P be any point on the circumference of the circle with diameter AB. If AP meets the other circle at Q, then
a) QC // PB
b) QC is never parallel to PB
c) QC =$\ \frac{1}{2}\ $PB
d) QC // PB and QC = $\ \frac{1}{2}\ $PB
Question 23: An isosceles triangle ABC is right angled at B.D is a point inside the triangle ABC. P and Q are the feet of the perpendiculars drawn from D on the sides AB and Ac respectively of $\ \triangle ABC.\ $If AP = a cm, AQ = b cm and $\ \angle BAD$= 15$^\circ$, sin $\ 75^\circ$=
a) $\frac{2b}{\sqrt{3a}}$
b) $\frac{a}{2b}$
c) $\frac{\sqrt{3a}}{2b}$
d) $\frac{2a}{\sqrt{3b}}$
Question 24: Each interior angle of a regular octagon in radians is
a) $\frac{\pi}{4}$
b) $\frac{3\pi}{4}$
c) $\frac{2\pi}{3}$
d) $\frac{1}{3}\pi$
Question 25: Find the value of $\ \sqrt{30+\sqrt{30}+…}$
a) 5
b) 3
c) 6
d) 7
Instructions
Select the related word/number from the given alternatives.
Question 26: Brain : Nerves : : Computer ?
a) Calculator
b) Keyboard
c) Mouse
d) CPU
Question 27: Silkworm : Silk Saree : : Cobra 😕
a) Antidote
b) Poison
c) Death
d) Fear
Instructions
Find the odd word from the given alternatives.
Question 28:
a) Cover
b) Enclose
c) Bag
d) Annex
Question 29: a: Illusion
b: Delusion
c: Identification
d: Hallucination
a) A
b) B
c) C
d) D
Question 30: Arrange the following words according to dictionary:
1: Inadequate
2: Institution
3: Inhospitable
4: Improvement
a) 4, 2, 3, 5, 1
b) 4, 1, 3, 5, 2
c) 4, 1, 5, 3, 2
d) 4, 1, 5, 2, 3
1500+ Free SSC Questions and Answers
Question 31: Identify the correct answer containing letters which will most appropriately fill in the blanks.
a b a – a b – b – b a –
a) a, a, a, b
b) b, a, b, a
c) b, a, a, b
d) a, b, b, b
Instructions
Select the missing letter/number from the given responses.
Question 32: ?, 187, 2057, 22627
a) 25
b) 27
c) 15
d) 17
Question 33: C, F, I, L, ?, R, U, X
a) A
b) T
c) M
d) O
Question 34: Nikhil was facing East. He walked 6 km forward and then after turning to his right walked 2 km. Again he turned to his right and walked 6 k. After this, he turned back. Which direction he was facing at that time ?
a) East
b) West
c) North
d) North-South
Question 35: Six boys are standing in such a manner that they form a circle facing the centre. Anand is to the left of Ravi. Shankar is in between Ajay and Vivek. Ishwar is between Anand and Ajay. Who is to the left of Vivek ?
a) Ravi
b) Ishwar
c) Ajay
d) Shankar
Question 36: From the given alternatives, select the word which cannot be formed using the letters of the given word.
CONSIDERATION
a) CONSIDER
b) CONCERN
c) NATIN
d) RATION
Question 37: If EARN is written as GCTP, how NEAR can be written in that code ?
a) CTGP
b) GPTC
c) PGCT
d) PCGT
Question 38: If AMPLIFY is written as YFILPMA In a certain code, how would NATIONAL be written in that code ?
a) LANONATI
b) LANOITAN
c) LANTANIO
d) LANTION
Question 39: The population of a developing country is increasing year by year. Find out the current year population, from the following information:
Year 2004 2005 2006 2007 2008 2009
Pop. in lakhs 30 60 120 210 230 ?
a) 390
b) 450
c) 480
d) 510
Question 40: Gokul travelled 16 kms west ward, then he turned left and travelled 10 kms. Then he turned left and travelled 16 kms. How far was Gokul from the starting point ?
a) 16 kms
b) 26 kms
c) 10 kms
d) 6 gkms
Answers & Solutions:
1) Answer (D)
Relative speed = (120 + 80) kmph (or) 200 kmph, Relative time = 9 seconds, Relative distance = (270 + x) meters
Let x be the length of other train.
We know that,
Distance = speed x time
270 + x = 200 x $\frac{5}{18}$ x 9
270 + x = 100 x 5
x = 500 – 270 (or) 230 meters.
Hence, option D is the correct answer.
2) Answer (B)
Principal sum = Rs. 10,000
Rate of interest = 10% and time period = 3 years
Amount after compound interest = $P(1+\frac{r}{100})^T$
= $10,000(1+\frac{10}{100})^3$
= $10,000\times(\frac{11}{10})^3$
= $10\times1331=Rs.$ $13,310$
=> Ans – (A)
3) Answer (A)
Let the number be $x$
According to ques,
=> $2\times(x)^2=(18)^3$
=> $(x)^2=(18)^2\times\frac{18}{2}$
=> $x=\sqrt{(18)^2\times9}$
=> $x=18\times3=54$
=> Ans – (A)
4) Answer (C)
Average salary of 27 people = Rs. 3700
=> Total salary of 27 people = $3700\times27=Rs.$ $99,900$
Let the salary of new person = Rs. $x$
According to ques,
=> $\frac{99,900+x}{28}=3750$
=> $99,900+x=3750\times28$
=> $x=1,05,000-99,900=5100$
$\therefore$ Salary of the new person = Rs. 5100
=> Ans – (C)
5) Answer (D)
$\frac{16}{x}=\frac{x}{42.25}$
==> $x^{2}=\frac{16\times4225}{100}$
==> $x=\frac{4\times65}{10}$
$\therefore x = 26$
6) Answer (C)
Let the amount distributed among P, Q and R be 5x, 9x and 17x respectively
Total shares of P and Q is 7,000 (given) i.e
$\Rightarrow$ 5x + 9x = 7,000
$\Rightarrow$ 14x = 7,000 (or) x = 500
$\therefore$ R’s share = 17(500) = 8,500
Hence, option C is the correct answer.
7) Answer (D)
Let the number be $x$
According to ques,
=> $\frac{1}{4}\times\frac{3}{5}\times(x)=42$
=> $x=42\times\frac{20}{3}$
=> $x=280$
$\therefore$ 40% of the number = $\frac{40}{100}\times280=112$
=> Ans – (D)
8) Answer (B)
To find : $10\%$ of $24.2-10\%$ of $24.02$
=> $(\frac{10}{100}\times24.2)-(\frac{10}{100}\times24.02)$
=> $2.42-2.402=0.018$
=> Ans – (B)
9) Answer (A)
Let tag price = Rs. $100x$
Discount % = 20%
=> Calculator’s selling price = Cost price for Ramesh = $100x-(\frac{20}{100}\times100x)$
= $100x-20x=Rs.$ $80x$
Profit = $\frac{10}{100}\times80x=Rs.$ $8x$
Also, selling price = $(80x+8x)=440$
=> $x=\frac{440}{88}=5$
$\therefore$ Tag price = $100\times5=Rs.$ $500$
=> Ans – (A)
10) Answer (A)
Let, the two numbers be x and y
Given, sum of two numbers (x + y) = 22 ……… (1)
Difference of two numbers (x – y) = 14 ………. (2)
By adding the above two equations we get,
2x = 36 (or) x = 18
By subtracting the above two equations we get,
2y = 8 (or) y = 4
Product of two numbers (x $\times$ y) = 18 x 4 = 72
Hence, option A is the correct answer.
11) Answer (B)
Given : $m=9$ and $n=\frac{1}{3}m$
=> $n=\frac{1}{3}\times9=3$
To find : $\sqrt{(m)^{2}-(n)^{2}}$
= $\sqrt{(9)^2-(3)^2}$
= $\sqrt{81-9}=\sqrt{72}=6\sqrt2$
=> Ans – (B)
12) Answer (B)
Let the present ages of x and y be 3a,4a respectively
After 5 years, their ages will be 3a+5 and 4a+5
$\frac{3a+5}{4a+5} = \frac{4}{5}$
==> 5(3a+5) = 4(4a+5)
==> 15a+25 = 16a+20
==> a=5
Present age of x = 3*5=15 years
Present age of y = 4*5=20 years
13) Answer (A)
14) Answer (C)
$2\frac{1}{5}x^{2}=2750$
==> $\frac{11}{5}x^{2}=2750$
==> $x^{2}= \frac{2750\times5}{11}$
==> $x^{2}= 1250$
==> $x = \sqrt{1250}=\sqrt{625\times2}$
==> $x = 25\sqrt{2}$
15) Answer (D)
$\frac{75\times75-26\times26}{101}$ = $ \frac{75^{2}-26^{2}}{101}$
==>$ \frac{(75+26)(75-26)}{101}$ ( $\because a^{2}-b^{2}=(a+b)(a-b)$)
= $\frac{101\times49}{101} = 49$
16) Answer (B)
Given that AB=BC=2a units and BC=a units
AD$\bot$BC $\Rightarrow$ ‘D’ is midpoint of BC
BD=DC=$\frac{a}{2}$
Here \triangle ABD is a right angled triangle where AB is hypotenuse
$AB^{2}$=$BD^{2}+AD^{2}$
$\Rightarrow AD^{2}$=$AB^{2}-BD^{2}$
$\Rightarrow AD$= $\sqrt{2a^{2}-\frac{a}{2}}$
= $\sqrt{4a^{2}-\frac{a^2}{4}}$
= $\sqrt{\frac{15a^{2}}{4}}$ = $\frac{\sqrt{15}a}{2}$ units
17) Answer (D)
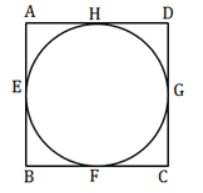
Given : AB = 6 cm. BC = 7.5 cm. CD = 3 cm
To find : DA = ?
Solution : Tangents from the same point to a circle are equal in length.
=> $AE=AH$, $BE=BF$, $CG=CF$ and $DG=DH$
Adding above equations, we get :
=> $(AE+BE)+(CG+DG)=(BF+CF)+(AH+DH)$
=> $AB+CD=BC+DA$
=> $6+3=7.5+DA$
=> $DA=9-7.5=1.5$ cm
=> Ans – (D)
18) Answer (C)
Let the sides of the triangle ABC(right angled at B) be ‘a’,’b’,’c’ and c is hypotenuse
Given that $a\times b=$ $\frac{c^{2}}{2}$ $\Rightarrow$ $ c^{2}$=2ab
We know that $c^{2}$=$a^{2}+b^{2}$
Substituting $c^{2}$ value in above equation
2ab$=a^{2}+b^{2}$
$\Rightarrow$ $a^{2}-2ab+b^{2}=0$
$\Rightarrow$ $(a-b)^{2}=0$
$\Rightarrow a=b$
In a triangle, if two sides are equal then the opposite angles must be equal
We know that $\angle A+\angle B+\angle C=180^\circ$
Here $\angle A$=$\angle C$
$90^\circ+2\angle A$=$180^\circ$
$\therefore \angle A$=$\angle C$=$45^\circ$
19) Answer (D)
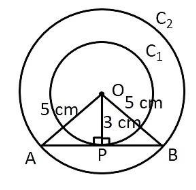
Given : $C_1$ and $C_2$ be the two concentric circles having radius $r_1=3$ cm and $r_2=5$ cm respectively.
To find : AB = ?
Solution : AB is the the tangent to the circle $C_1$, hence $\angle$ OPB = $90^\circ$
Also, the perpendicular from the centre of a circle to a chord bisects the chord.
Thus, in $\triangle$ OPB,
=> $(PB)^2=(OB)^2-(OP)^2$
=> $(PB)^2=(5)^2-(3)^2$
=> $(PB)^2=25-9=16$
=> $PB=\sqrt{16}=4$ cm
$\therefore$ AB = $2\times4=8$ cm
=> Ans – (D)
20) Answer (B)
In square ABCD, $\triangle$ BEC is an equilateral triangle
Each angle of an equilateral triangle is 60$^\circ$
$\Rightarrow$ $\angle$ OCB $= 60^\circ$
$\angle$ DBC $= \frac{90^\circ}{2} = 45^\circ$ ($\because$ BD is diagonal of ABCD)
In $\triangle$ OBC,
$\angle$ OBC+$\angle$ OCB+$\angle$ BOC $= 180^\circ$
$60^\circ+45^\circ+\angle BOC = 180^\circ$
$\therefore \angle BOC = 75^\circ$
21) Answer (A)
$\triangle$ ABC is a right angled triangle right angled at C
$\Rightarrow$ $AB^{2} = AC^2+BC^2$ ( From Pythagoras theorem )
$\Rightarrow$ $AC^2 = AB^2-BC^2$
From $\triangle ACD$, $AD^2 = AC^2+CD^2$
Substituting $AC^2 = AB^2-BC^2$ in above equation
$AD^2 = AB^2-BC^2+CD^2$
$\Rightarrow$ $AB^{2}+CD^{2}=BC^{2}+AD^{2}$
SSC GD Important Questions & Answers PDF
22) Answer (A)
In $\triangle$ AQC,
$\angle$ AQC $= 90^\circ$ ($\because$ Angle in a semi circle is $90^\circ$)
and in $\triangle$ APB,
$\angle$ APB $= 90^\circ$ ($\because$ Angle in a semi circle is $90^\circ$)
Comparing two triangles $\triangle$ APB and $\triangle$ AQC,
$\angle$ QAC $= \angle PAB$
$\angle$ AQC $= \angle APB$
$\therefore \triangle APB = \triangle AQC$
$\therefore$ QC // PB
Since we cannot prove that C is exactly midpoint of AB, QC $= \frac{1}{2}$PB cannot be proved
23) Answer (C)
$\triangle$ ABC is a right angled isosceles triangle right angled at B
Here $\angle A = \angle C$
$90^\circ+2\angle A = 180^\circ$
$\therefore \angle A = \angle C = 45^\circ$
Given $\angle BAD = 15^\circ$
From $\triangle$ ABC, $\angle BAC = \angle BAD+\angle DAQ$
$\Rightarrow 45^\circ = 15^\circ+\angle DAQ$
$\therefore \angle DAQ = 30^\circ$
From $\triangle DAQ, \angle AQD = 90^\circ$ and $\angle DAQ = 30^\circ$
$\angle AQD+\angle DAQ+\angle ADQ = 180^\circ$
$90^\circ+30^\circ+\angle ADQ = 180^\circ$
$\Rightarrow \angle ADQ = 60^\circ$
$From \triangle ADQ$,
sin $60^\circ = \frac{AQ}{AD}$
$\frac{\sqrt{3}}{2} = \frac{b}{AD}$ ( $\because$ sin $60^\circ = \frac{\sqrt{3}}{2})$
AD = $\frac{2b}{\sqrt{3}}$
In $\triangle APD, \angle APD = 90^\circ$ and $\angle PAD = 15^\circ$
$\angle APD+\angle PAD+\angle ADP = 180^\circ$
$90^\circ+15^\circ+\angle ADP = 180^\circ$
$\Rightarrow \angle ADP = 75^\circ$
From $\triangle$ APD,
sin $75^\circ = \frac{AP}{AD}$
Substituting AD = $\frac{2b}{\sqrt{3}}$ in above equation
$\Rightarrow$ sin $75^\circ = \frac{a}{(\frac{2b}{\sqrt{3}})}$
$\therefore$ sin $75^\circ = \frac{\sqrt{3}a}{2b}$
24) Answer (B)
Each angle of a regular Octagon = $\frac{1}{8}(2n-4)$right angle where n=no. of sides
= $\frac{1}{8}(2\times8-4)\times90^\circ$
= $\frac{12\times90^\circ}{8}$=$135^\circ$
$180^\circ$=$\prod$
$135^\circ$=$\frac{\prod}{180}\times135^\circ$=$\frac{3\prod}{4}$
25) Answer (C)
Let X=$ \sqrt{30+\sqrt{30}+…}$
Above equation can be written as
X=$\Rightarrow\sqrt{30+X}$
Squaring on both sides
$X^{2}$=30+X
$X^{2}$-X-30=0
$X^{2}$-6X+5X-30=0
X(X-6)+5(X-6)=0
(X-6)(X+5)=0
X=-5,6
Taking positive value
X=6
26) Answer (D)
Nerves helps the brain to function in the same way CPU helps the computer to function.
Hence, option D is the correct answer.
27) Answer (B)
Silkworm produces silk whereas cobra produces poison.
Hence, option B is the correct answer.
28) Answer (C)
29) Answer (C)
All the given words are synonyms except ‘Identification’
Hence, option C is the correct answer.
30) Answer (C)
31) Answer (C)
The pattern followed here is,
a b a b a b a b a b a b (repeating ‘ab’ for 6 times). Option C exactly fits in the blanks.
Hence, option C is the correct answer.
32) Answer (D)
Every number is multiplied by 11.
17 x 11 = 187,
187 x 11 = 2057,
2057 x 11 = 22627.
Hence, option D is the correct answer.
33) Answer (D)
The pattern followed here is,
C + 2 = F,
F + 2 = I,
I + 2 = L,
L + 2 = O………
Hence, option D is the correct answer.
34) Answer (A)

Nikhil faces East finally after turning back.
Hence, option A is the correct answer.
35) Answer (A)
Anand is to the left of Ravi. Ishwar is between Anand and Ajay. From this conditions arrangement will be,
_Zt4XYwr.PNG)
Shankar is in between Ajay and Vivek. Final arrangement will be,
.PNG)
From the above arrangement,
Ravi is to the left of vivek.
Hence, option A is the correct answer.
36) Answer (B)
37) Answer (C)
The pattern followed here is,
E + 2 = G ; A + 2 = C ; R + 2 = T ; N + 2 = P i.e (n + 2)
NEAR is coded as,
N + 2 = P ; E + 2 = G ; A + 2 = C ; R + 2 = T
NEAR – PGCT
Hence, option C is the correct answer.
38) Answer (B)
The positions of alphabets in the given word are reversed.
Hence, the code for NATIONAL will be LANOITAN
Hence, option B is the correct answer.
39) Answer (C)
40) Answer (C)
From the given information,

Gokul was 10 kms far from his starting point.
Hence, option C is the correct answer.
Download SSC GD Previous Papers PDF
DOWNLOAD APP FOR SSC FREE MOCKS
We hope this Quant questions for SSC GD will be highly useful for your preparation.





