SSC CGL TIER-1 9th March 2020 shift -3 Quantitative aptitude questions with detailed solutions.
SSC CGL Previous Year Quant Paper: A study plan for cracking the SSC CGL Exam must include the daily task of practising Previous Year Question Papers. Students can attempt all four sections (General Intelligence & Reasoning, General Awareness & GK, Quantitative Aptitude and English Language & Comprehension) and build an innovative preparation strategy to clear this exam with a high score. Here you can download SSC CGL TIER-1: 9th March 2020 Shift -3 Quantitative aptitude questions with detailed solutions.
Download SSC CGL Previous Year Quant Questions with Solutions
Watch Video Explanation :
Question 1: The value of $\frac{3(1 – 2 \sin^{2}x)}{\cos^{2}x – \sin^{2}x}$ is:
a) 4
b) 3
c) 1
d) 2
Question 2: The perimeter of a square plot is the same as that of a rectangular plot with sides 35 m and 15 m. The side of the square plot is:
a) 25 m
b) 20 m
c) 100 m
d) 50 m
Question 3: The value of $515\times485$ is:
a) 249775
b) 250225
c) 20825
d) 200825
Question 4: The following table shows the number of students enrolled in different streams in a particular college.

The ratio of the number of girls studying Arts to the number of girls studying in all other streams is:
a) 1 : 3
b) 2 : 1
c) 1 : 2
d) 3 : 1
Question 5: The compound interest on a certain sum at the end of two years is Rs.408. The simple interest on the same sum for the same time is Rs.400. The rate of interest per annum is:
a) 2%
b) 80%
c) 40%
d) 8%
Question 6: A car dealer purchased an old car for Rs.1,08,500 and spent some amount on its maintenance. He sold it for Rs.1,56,250, there by earning a profit of 25%. How much money did he spend on the maintenance of the car?
a) Rs. 16,500
b) Rs. 20,625
c) Rs. 8,687.5
d) Rs. 47,750
Question 7: The following table gives the frequency of vowels used in the page of a book.

As per the given data, which vowels occur less than 80 times?
a) a, e, i
b) a, i, o, u
c) a, o, u
d) a, e
Question 8: Eight persons can finish a work in 20 days. After 5 days they were requested to complete the work in the next 8 days. How many more persons should join the group to fulfil the requirement?
a) 23
b) 15
c) 7
d) 12
Question 9: The following table shows the income(in rupees) for a particular month, together with their source, in respect of 5 employees (A, B, C, D and E).
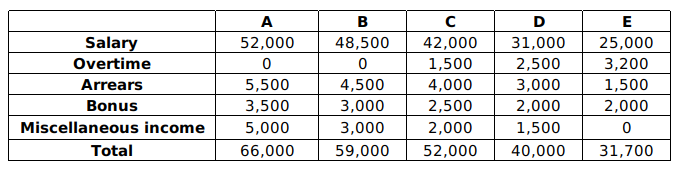
For employee D, the income from overtime is what percentage of his total income?
a) 5%
b) 7.5%
c) 6.25%
d) 22.5%
Question 10: Ina class, the average score of thirty students on a test is 69. Later on it was found that the score of one student was wrongly read as 88 instead of 58. The actual average score is:
a) 58
b) 88
c) 69
d) 68
Question 11: PAQ is a tangent to circle with centre O, at a point A on it. AB is a chord such that $\angle BAQ = x^\circ(x < 90)$. C is a point on the major arc AB such that $\angle ACB = y^\circ$. If $\angle ABO = 32^\circ$, then the value of $x + y$ is:
a) 98
b) 112
c) 110
d) 116
Question 12: The smallest number which may replace * in the number 1190*6 to make the number divisible by 9 is:
a) 1
b) 9
c) 3
d) 0
Question 13: The value of $(26-13\times2)\div2+1$ is:
a) $0$
b) $1$
c) $\frac{26}{3}$
d) $14$
Question 14: The value of $\cos 10^\circ \cos 30^\circ \cos 50^\circ \cos 70^\circ \cos 90^\circ$ is:
a) 3
b) 0
c) 5
d) 1
Download SSC CHSL Previous Papers PDF
Download SSC CGL Previous Papers PDF
Question 15: A cell phone was marked at 20% above the cost price and a discount of 10% was given on its marked price. What is the profit percentage?
a) 10%
b) 8%
c) 11%
d) 9%
Question 16: The value of $(\cosec 30^\circ – \tan 45^\circ) \cot 60^\circ \tan 30^\circ$ is:
a) $\frac{1}{3}$
b) $1$
c) $3$
d) $\frac{1}{\sqrt{3}}$
Question 17: If $x+3y+2=0$ then value of $x^{3}+27y^{3}+8-18xy$ is:
a) -2
b) 2
c) 1
d) 0
Take a free SSC CGL Tier-1 mock test
Take a free SSC CHSL Tier-1 mock test
Question 18: As per data shown in the following table, what is the percentage of students who got less than 50 marks?

a) 74%
b) 48%
c) 72%
d) 38%
Question 19: In the triangle, If $AB = AC$ and $\angle ABC = 72^\circ$, then $\angle BAC$ is:
a) $36^\circ$
b) $30^\circ$
c) $54^\circ$
d) $18^\circ$
Question 20: In a circle, AB is a the diameter and CD is a chord. AB and CD produced meet at a point P, outside the circle. If PD = 15.3 cm, CD = 11.9 cm and AP = 30.6 cm,then the radius of the circle is is:
a) 8 cm
b) 8.5 cm
c) 9cm
d) 7.5 cm
Question 21: From an external point P, a tangent PQ is drawn to a circle, with the centre O, touching the circle at Q. If the distance of P from the centre is 13 cm and length of the tangent PQ is 12 cm, then the radius of the circle is:
a) 3cm
b) 5 cm
c) 10 cm
d) 12.5 cm
Question 22: If $p+q=7$ and $pq=5$, then the value of $p^{3}+q^{3}$ is:
a) 34
b) 238
c) 448
d) 64
Question 23: If an amount of Rs.990 is divided among A, B and C in the ratio of 3 : 4 : 2, then B will get:
a) Rs. 247.5
b) Rs. 440
c) Rs. 110
d) Rs. 350
Question 24: The price of cooking oil increased by 25%. Find by how much percentage a family must reduce its consumption in order to maintain the same budget?
a) 70%
b) 80%
c) 30%
d) 20%
Question 25: The distance between two stations A and B is 575 km. A train starts from station ‘A’ at 3:00 p.m. and moves towards station ‘B’ at an average speed of 50 km/h. Another train starts from station ‘B’ at 3:30 p.m. and moves towards station ‘A’ at an average speed of 60 km/h. How far from station ‘A’ will the trains meet ?
a) 275 km
b) 325 km
c) 300 km
d) 225 km
Take a free SSC CGL Tier-1 mock test
Take a free SSC CHSL Tier-1 mock test
Answers & Solutions:
1) Answer (B)
$\frac{3(1-2sin^{2}x)}{cos^{2}x-sin^{2}x}$
= $\frac{3(1-2sin^{2}x)}{1-sin^{2}x-sin^{2}x}$
($\because sin^{2}x + cos^{2}x = 1$)
= $\frac{3(1-2sin^{2}x)}{1-2sin^{2}x}$ = 3
2) Answer (A)
The perimeter of a rectangular plot = 2(length + breadth) = 2(35 + 15) = 100 m
The perimeter of a square plot = perimeter of a rectangular plot
The perimeter of a square plot = 100 m
100 = 4 $\times$ side
side = 100/4 = 25 m
3) Answer (A)
$515\times485$
= $(500 + 15)\times(500 – 15)$
= $(500)^2 – (15)^2$
($\because (a – b)(a + b) = a^2 – b^2$)
= 250000 = 225 = 249775
4) Answer (C)
Number of girls studying Arts = 45
Number of girls studying in all other streams = 18 + 42 + 30 = 90
The ratio of the number of girls studying Arts to the number of girls studying in all other streams = 45 : 90 = 1 : 2
5) Answer (A)
Difference of interest = 408 – 400 = 8
In the 2nd year, extra interest counts on the interest of the 1st year so.
Interest = $\frac{prt}{100}
8 = $\frac{400 \times r \times 1}{100}$
r = 2%
6) Answer (A)
Total cost price of old car = 1,08,500 + maintenance money
Selling price = 1,56,250
Profit = 25%
Total cost price = $\frac{156250}{125} \times 100 = 125000
1,08,500 + maintenance money = 125000
Maintenance money = 125000 – 108500 = Rs. 16,500
7) Answer (C)
Vowels occur less than 80 times = a, o, u
8) Answer (C)
Total work = number of persons $\times time = 8 \times 20 = 160$
Work done in 5 days = 8 $times 5 = 40$
Remaining Work = 160 – 40 = 120
According to question,
Number of man $\times$ time = 120
Number of man $\times$ 8 = 120
Number of man = 120/8 = 15
Number of persons should join the group = 15 – 8 = 7
9) Answer (C)
Total income of employee D = 40000
Income from overtime of employee D = 2500
Required percentage = $\frac{2500}{40000} \times 100 = 6.25%
10) Answer (D)
When data read wrongly then total score of thirty students on a test = 69 $\times$ 30 = 2070
(Average = sum of all terms/number of terms)
Difference in data = 88 – 58 = 30
Actual score = 2070 – 30 = 2040
Actual average score = 2040/30 = 68
11) Answer (D)
Download SSC CGL Previous Papers PDF
Download SSC CHSL Previous Papers PDF
12) Answer (A)
By the divisibility rule, if sum of all digits of a number is divisible by 9 the number will be divisible by 9.
Number =1190*6
Sum of the digits = 1 + 1+ 9 + 0 + * + 6 = 17 + *
For the smallest number, we took the minimum value of the ‘*’.
so, value of * = 1
Sum of all digit = 17 + 1 = 18
$\therefore$ the value of * will be 1.
13) Answer (B)
$(26-13\times2)\div2+1$
= $(26- 26)\div2+1$ = 0 + 1 = 1
14) Answer (B)
$cos10^{0}cos30^{0}cos50^{0}cos70^{0}cos90^{0}$
= $cos10^{0}cos30^{0}cos50^{0}cos70^{0}\times 0$
($\because cos90^{0} = 0$)
= 0
15) Answer (B)
Let the cost price be 100.
Marked price = 100 $\times$ 120/100 = 120
Discount = 10%
Selling price = 120 $\times 90/100 = 108
Profit = 108 – 100 = 8
Profit percentage = $\frac{8}{100} \times$ 100 = 8%
16) Answer (A)
$(\cosec 30^\circ – \tan 45^\circ) \cot 60^\circ \tan 30^\circ$
On put the value,
= $(2 – 1)\frac{1}{\sqrt3} \times \frac{1}{\sqrt3}$
= 1/3
17) Answer (D)
$x+3y+2=0$
x + 3y = -2
Taking cube both sides,
$(x + 3y)^3 = -8$
$x^3 + 27y^3 + 3x.3y(x + 3y) = -8$
$x^3 + 27y^3 + 9xy(-2) = -8 $
$x^{3}+27y^{3} -18xy = -8$
$x^{3}+27y^{3}+8-18xy$ = 0
18) Answer (B)
Number of students who got less than 50 marks = 5 + 11 + 18 + 38 = 72
Total number of students = 5 + 11 + 18 + 38 + 39 + 24 + 15 = 150
Percentage of students who got less than 50 marks = $\frac{72}{150} \times 100$ = 48%
19) Answer (A)
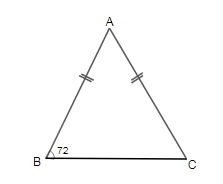
By triangle properties,
When AB = AC then $\angleABC = \angleACB$ so,
In$\triangle$ ABC,
$\Rightarrow$ $ \angle ABC + \angle ACB + \angle BAC = 180^{0}$
$\Rightarrow \angle ABC + \angle ABC + \angle BAC = 180^{0}$
$\Rightarrow 72^{0} + 72^{0} + \angle BAC = 180^{0}$
$\Rightarrow \angle BAC = 180^{0} – 144^{0} = 36^{0}$
20) Answer (B)
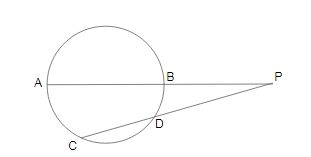
From the property,
PA $\times PB = PC \times PD$
30.6 $\times PB = (PD + CD) \times 15.3$
30.6 $\times PB = (15.3 + 11.9) \times 15.3$
30.6 $\times PB = 27,2 \times 15.3$
PB = 416.16/30.6 = 13.6 cm
Diameter (AB) = PA – PB = 30.6 – 13.6 = 17 cm
Radius = AB/2 = 17/2 = 8.5 cm
21) Answer (B)
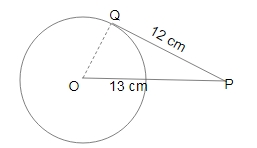
$\triangle$ OPQ is a right angle triangle because $\angle Q = 90\degree$,
By Pythagoras,
$(OQ)^2 + (PQ)^2 = (OP)^2$
$(OQ)^2 = (13)^2 – (12)^2$
$(OQ)^2 = 169 – 144$
$(OQ)^2 = 25$
$OQ = 5$
$\therefore$ The radius of the circle is 5 cm.
22) Answer (B)
$p^{3}+q^{3} = (p + q)^3 – 3pq(p + q)$
=$7^3 – 3 \times 5(7)$
= 343 – 105 = 238
23) Answer (B)
Ratio of the A, B and C = 3 : 4 : 2
Amount = 990
Share of B = $\frac{4}{3 + 4 + 2} \times 990 = \frac{4}{9} \times 990 = Rs.440
24) Answer (D)
By the formula,
Decrements in the consumption in order to maintain the same budget = $\frac{increment in the rate}{100 + increment in the rate} \times 100$
= $\frac{25}{100 + 25} \times 100 = \frac{25}{125} \times 100 = 20%
25) Answer (A)
Distance between stations = 575 km
Speed of train A = 50 km/hr
Distance covered by train A in (30 min = 1/2 hr) = time $\times speed = 50 \times 1/2 = 25 km$
Trains are running in opposite direction so,
Relative speed = 50 + 60 = 110 km/hr
Distance covered by both train = 575 – 25 = 550 km
Time taken by both trains to meet = 550/110 = 5 hr
Distance covered by train A in 5 hr = 5 $\times 50 = 250 km$
Distance covered by train A from station A = distance covered by train A in 30 min + distance covered by train A in 5 = 250 + 25 = 275 km
$\therefore$275 km far from station ‘A’ will the trains meet.





