SNAP Mensuration Questions PDF [Most Important]

Mensuration is an important topic in the Quant section of the SNAP Exam. You can also download this Free Mensuration Questions for SNAP PDF (with answers) by Cracku. These questions will help you to practice and solve the Mensuration questions in the SNAP exam. Utilize this PDF practice set, which is one of the best sources for practising.

Download Mensuration Questions for SNAP

Enroll to SNAP 2022 Crash Course

Question 1: Three cubes each having volume 1728 $cm^{3}$ are placed one above the other. What is the total surface area of the resulting solid?

a) 2304 $cm^{2}$

b) 2592 $cm^{2}$

c) 2160 $cm^{2}$

d) 2016 $cm^{2}$

1) Answer (D)

Solution:

Given,

Volume of Each cube = $1728\ cm^3$

Volume of cube = $\left(side\right)^3$

$\left(side\right)^3=1728$

$\left(side\right)=\ 12$

When three cubes are placed one over another it formed a Cuboid as shown in figure.

Now, l =12 , b =12 , h = 36

Volume of Cuboid = 2(lb + bh + hl)

= 2($\left(12\times\ 12\right)+\left(12\times\ 36\right)+\left(36\times\ 12\right)$)

= 2 (144 + 432 + 432)

= 2 ( 1008 )

= 2016 $cm^3$

Hence, Option D is correct.

Question 2: The sum of the cubes of two numbers is 128, while the sum of the reciprocals oftheir cubes is 2.
What is the product of the squares of the numbers?

a) 64

b) 256

c) 16

d) 48

e) 32

2) Answer (C)

Solution:

Considering the two numbers to a, b :

We were given that :

$a^3+b^3\ =\ 128$

$\frac{1}{a^3}+\ \frac{1}{b^3}=\ 2$

$\frac{\left(a^3+b^3\right)}{a^3\cdot b^3}=\ 2\ =\ \frac{128}{k}$

k = 64.

Hence $a^3\cdot b^3\ =\ 64$

a*b = 4 and $a^2\cdot b^2\ =\ 16$

Question 3: The surface area of a cube is 13.5 m$^2$. What is the length (in m) of its diagonal?

a) $2\sqrt{3}$

b) $1.5\sqrt{3}$

c) 1.5

d) 2

3) Answer (B)

Solution:

Let the side of the cube = a

The surface area of a cube is 13.5 m$^2$.

6a$^2$ = 13.5

12a$^2$ = 27

a$^2$ = $\frac{9}{4}$

a = $\frac{3}{2}$

a = 1.5 m

Length of the diagonal of the cube = $\sqrt{3}$a

= 1.5$\sqrt{3}$ m

Hence, the correct answer is Option B

Question 4: The surface area of the resultant cuboid that gets formed by placing five ice cubes adjacent to each other, each of whose side is 5 centimetres, is _____________.

a) 625 cm$^{2}$

b) 550 cm$^{2}$

c) 125 cm$^{2}$

d) 650 cm$^{2}$

4) Answer (B)

Solution:

The dimensions of given cuboid is 25 cm, 5 cm and 5 cm

Surface area = 2(lb+bh+lh) = 2(125 + 125 + 25) = 550 $cm^2$

Answer is option B.

Question 5: The volume of a cube is 343 cm$^3$. The edge of cube is:

a) 7 cm

b) 6 cm

c) 5 cm

d) 4 cm

5) Answer (A)

Solution:

Let the edge of the cube = a

Volume of the cube = a$^3$

Given, Volume of the cube = 343 cm$^3$

$\Rightarrow$ a$^3$ = 343

$\Rightarrow$ a$^3$ = 7$^3$

$\Rightarrow$ a = 7 cm

$\therefore\ $Edge of the cube = 7 cm

Hence, the correct answer is Option A

Question 6: The curved surface are of a right circular cone is 65 $\pi$ $cm^{2}$ and the radius of its base in 5 cm. What is half of the volume of the cone, in $cm^{3}$ ?

a) 50 $\pi$

b) 100 $\pi$

c) 180 $\pi$

d) 45 $\pi$

6) Answer (A)

Solution:

Given,

Radius = 5 cm

Curved surface area = $\pi\ \times\ r\times\ l=65\pi\ $

$\pi\ \times\ 5\times\ l=65\pi\ $

by solving , we get , $l=13$

as shown in the figure, l = slant height, r = radius of cone, h = height of cone

We know, $l^2\ =\ r^2+\ h^2$

$\therefore13^2\ =\ 5^2+\ h^2\ $

By solving , we get h = 12

According to question ,

Half of the volume = $\frac{1}{2}\times\ \frac{1}{3}\times\ \pi\ \times\ r^2\times\ h$

$=\ \frac{1}{2}\times\ \frac{1}{3}\times\ \pi\ \times\ 5^2\times\ 12$

$=50\ \pi\ $

Hence, Option A is correct.

Take  SNAP mock tests here

Enrol to 10 SNAP Latest Mocks For Just Rs. 499

Question 7: The curved surface area of a right circular cone is 65 $\pi$ $cm^{2}$ and the radius of its base is 5 cm. What is 40% of the volume of the cone, in $cm^{3}$?

a) 50 $\pi$

b) 40 $\pi$

c) 180 $\pi$

d) 100 $\pi$

7) Answer (B)

Solution:

Given,

Curved Surface Area (C.S.A) of cone = 65$\pi\ $’

We know,

C.S.A of cone = $\pi rl$

$\pi\times\ 5\times\ l=65\pi\ $

$l=13\ cm$

$\therefore\ l^2=h^2+r^2$

$\therefore\ 13^2=h^2+5^2$

by solving, We get h = 12cm

Now, Volume of cone = $\frac{1}{3}\pi\ r^2h$

$\therefore\ $ 40% of volume of cone = $\frac{40}{100}\times\ \frac{1}{3}\pi\ r^2h$

$\therefore\ \frac{4}{10}\times\ \frac{1}{3}\times\pi\ \times25\times\ 12\ $

= 40$\pi\ $

Hence, Option B is correct.

Question 8: A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is

a) 243

b) 232

c) 256

d) 264

8) Answer (A)

View Video Solution

Solution:

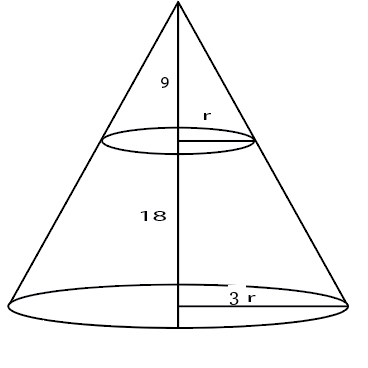
Let the base radius be 3r.

Height of upper cone is 9 so, by symmetry radius of upper cone will be r.

Volume of frustum=$\frac{\pi}{3}\left(9r^2\cdot27-r^2.9\right)$

Volume of upper cone = $\frac{\pi}{3}.r^2.9$

Difference= $\frac{\pi}{3}\cdot9\cdot r^2\cdot25=225$ => $\frac{\pi}{3}\cdot r^2=1$

Volume of larger cone = $\frac{\pi}{3}\cdot9r^2\cdot27=243$

Question 9: The radius of a circular cone is 6 cm and its height is 7 cm. Then the volume of cone in $cm^3$ is: (Take $\pi = \frac{22}{7}$)

a) 216

b) 154

c) 264

d) 188

9) Answer (C)

Solution:

Given,

Radius of the circular cone (r) = 6 cm

Height of the circular cone (h) = 8 cm

$\therefore\ $Volume of the circular cone = $\frac{1}{3}\pi\ r^2h=\frac{1}{3}\times\frac{22}{7}\times\left(6\right)^2\times7=264\ cm^3$

Hence, the correct answer is Option C

Question 10: The radius of the base of a cylinder is $\frac{1}{3}$ of the radius of the base of a cone .If their heights are equal, then the ratios of their voulumes is

a) 1:3

b) 2:3

c) 2:5

d) 3:2

10) Answer (A)

Solution:

Question 11: A cylinder and a cone have the same height and the same radius of the base. The ratio of the volumes of the cone and cylinder is

a) 1:3

b) 2:3

c) 3:4

d) 4:3

11) Answer (A)

Solution:

we know that

the volume of the cone is  =  1\3 $\times$ $\pi$ $\times$ r^2 $\times$ h    and

the volume of the cylinder is =   $\pi$ $\times$ r^2 $\times$ h  then

volume of the cone \ volume of the cylinder =  1\3 $\times$ $\pi$ $\times$ r^2 $\times$ h \ $\pi$ $\times$ r^2 $\times$ h

volume of the cone \ volume of the cylinder = 1\3   Answer

Question 12: The radius of a coneis 3 times the radius of a cylinder and their heights are same. Then the ratio of their volumesin that order is

a) 9 : 1

b) 1 : 3

c) 3 : 1

d) 1 : 9

12) Answer (C)

Solution:

Solution:

The radius of the cone is 3 times the radius of the cylinder and their heights are same.

Volume of cone = $\frac{1}{3}\pi\ R^2h$

Volume of cylinder = $\pi r^2h$

Given, R= 3r

So,Volume of cone = $\frac{1}{3}\pi\ (3r)^2h$

Ratio of volumes =  $\frac{1}{3}\pi\ (3r)^2h$ : $\pi r^2h$ = 3:1 Answer

Question 13: The curved surface area of a cone is 4070 sq. cm. If the diameter of the base of that cone is 70 cm, then its slant height in centimeters is

a) 22

b) 37

c) 44

d) 23

13) Answer (B)

Solution:

Question 14: A right circular cylinder with its diameter equal to its height is incribed in a right circular cone. The base radius and altitude of the cone are 5 cm and 12 cm respectively, and axes of cylinder and cone consider the diameter of the cylinder is

a) $\frac{30}{11}$ cm

b) $\frac{60}{11}$ cm

c) $\frac{30}{17}$ cm

d) $\frac{60}{17}$ cm

14) Answer (B)

Solution:

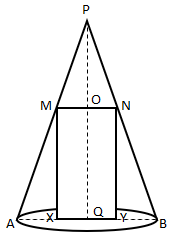
Base radius of cone = AQ = BQ = 5 cm

AB = 2AQ = 10 cm

Height of cone = PQ = 12 cm

Let QY = x and OQ = 2x

MN = XY = 2x

Now,

$\frac{MN}{AB} = \frac{PO}{PQ}$

$\frac{2x}{10} = \frac{12 – 2x}{12}$

6x = 30 – 5x

$x = \frac{30}{11}$

Ddiameter of the cylinder = XY = 2x = $\frac{60}{11} cm$

Question 15: A solid cylinder of lead 8 m and 2 m radius is melted and recast into a cone of radius 1.5 m. What is the height of the cone?

a) 16.67 m

b) 21.35 m

c) 42.67 m

d) 31.35 m

15) Answer (C)

Solution:

Let the height of cone = ‘h’ cm

Volume of cylinder = Volume of cone

$\pi * 2^2 * 8 = \frac{1}{3} * \pi * 1.5^2 * h$

3 * 4 * 8 = 1.5 * 1.5 * h

h = 42.67 m

Enroll to SNAP & NMAT 2022 Crash Course

Enroll to CAT 2022 course