Simplification Questions For SSC MTS
Download Top-20 SSC MTS Simplification Questions PDF. Simplification questions based on asked questions in previous year exam papers very important for the SSC MTS exam.
Download Simplification Questions For SSC MTS
Take a free mock test for SSC MTS
SSC MTS Previous Papers (Download PDF)
Question 1: Which of the following statements(S) is/are TRUE ?
I. $\sqrt[3]{512}\times\sqrt{256}>\sqrt[3]{343}\times\sqrt{289}$
II. $\sqrt{121}+\sqrt[3]{1331}>\sqrt[3]{125}\times\sqrt{25}$
a) Only I
b) Only II
c) Neither I nor II
d) Both I and II
Question 2: Which of the following is the largest number among $\sqrt{2},\sqrt[3]{2},\sqrt{4},\sqrt[3]{5}$
a) $\sqrt{2}$
b) $\sqrt[3]{3}$
c) $\sqrt{4}$
d) $\sqrt[3]{5}$
Question 3: What is the value of $\sqrt{{2^{6}}+15^2}$
a) 17
b) 19
c) 15
d) 21
Question 4: Rohit buys a ball for Rs 450 and sells it. Rohit gives two successive discount of 20% and 5% to the customer. What will be the selling price (in Rs) of the ball?
a) 342
b) 354
c) 334
d) 362
Question 5: $(4\sqrt{y^{8}})=225$
a) 10
b) 12
c) 15
d) 18
Take a free mock test for SSC MTS
Question 6: What is the value of $\sqrt[3]{729}\times\sqrt{16}+\sqrt{676}+\sqrt{169} ?$
a) 75
b) 64
c) 35
d) 60
Question 7: Manoj walks 12 metres towards north. Then turns right and walk another 12 metres. Then turn right and walks for 7 metres to reach college R. He again turns to his right and walks for 12 metres. What is the straight line distance (in metres) between the starting point and college R?
a) $12\sqrt2$
b) $13$
c) $14$
d) $14\sqrt3$
Question 8: Which of the following statement(s) is/are TRUE ?
I. $\sqrt{324}+\sqrt{3.24}+\sqrt{0.0324} = 19.98$
II. $\sqrt{129+\sqrt{121}+\sqrt{361}+\sqrt{100}}=13$
a) Only I
b) Only II
c) Neither I nor II
d) Both I and II
Question 9: What is the simplified value of $2\sqrt[3]{243}+3\sqrt[3]{9}-\sqrt[3]{1125}$ ?
a) $5\sqrt[3]{9}$
b) $4\sqrt[3]{9}$
c) $7\sqrt[3]{9}$
d) $11\sqrt[3]{9}$
Question 10: If $x=\frac{\sqrt{5}+1}{\sqrt{5}-1}$ and $y=\frac{\sqrt{5}-1}{\sqrt{5}+1}$, then what is the value of x-y ?
a) $3$
b) $\sqrt5$
c) $2\sqrt5$
d) $6$
SSC Study Material (18000 Solved Questions)
General Science Notes for SSC Exams
Question 11: If $x = 4 + \sqrt{15}$, then what is the value of $[x^2 + (\frac{1}{x^2})]$ ?
a) 62
b) 64
c) 34
d) 36
Question 12: If $p=\sqrt{72-\sqrt{72-\sqrt{72-\sqrt{72-……\infty}}}}$, then find the value of $2p^2+1$.
a) -129
b) -163
c) 129
d) 163
Question 13: If $4^x= \sqrt[7]{1024}$, then what is the value of X ?
a) $\frac{5}{7}$
b) $\frac{4}{7}$
c) $\frac{3}{7}$
d) $\frac{6}{7}$
Question 14: What is the value of $\sqrt[3]{512}+\sqrt{169}+\sqrt[3]{216}+\sqrt{225}$ ?
a) 48
b) 32
c) 42
d) 36
Question 15: If $x=\frac{4}{2\sqrt{3}+3\sqrt{2}}$,then find the value of $(x+\frac{1}{x})$
a) $\frac{(10\sqrt3+15\sqrt2)}{12}$
b) $\frac{(10\sqrt3-15\sqrt2)}{12}$
c) $\frac{-(10\sqrt3-33\sqrt2)}{12}$
d) $\frac{(10\sqrt3+33\sqrt2)}{12}$
Question 16: Which of the following statement(s) is/are CORRECT ?
I. $(\sqrt{11}+\sqrt{2})>(\sqrt{8}+\sqrt{5})$
II. $(\sqrt{10}+\sqrt{3})>(\sqrt{7}+\sqrt{6})$
a) Only I
b) Only II
c) Neither I nor II
d) Both I and II
Question 17: If $p+\frac{1}{p}=\sqrt{10}$, then find the value of $p^4+\frac{1}{p^4}$
a) 52
b) 60
c) 62
d) 65
Question 18: If $z=6-2\sqrt3$, then find the value of $(\sqrt{z}-\frac{1}{\sqrt{z}})^2$
a) $\frac{102-46\sqrt3}{4}$
b) $\frac{102-46\sqrt3}{2}$
c) $\frac{102-46\sqrt3}{24}$
d) $\frac{12-46\sqrt3}{24}$
Question 19: What is the positive square root of $[25+4\sqrt{39}]$ ?
a) $\sqrt{13}+2\sqrt3$
b) $\sqrt{13}+3\sqrt2$
c) $\sqrt{11}+2\sqrt3$
d) $11+3\sqrt2$
Question 20: If $x=\sqrt{15\sqrt{15\sqrt{15\sqrt{15\sqrt{15….\infty}}}}}$ and x>0, then find the value of $x^2+4$
a) 125
b) 179
c) 200
d) 229
200+ SSC Important Practice Sets
General Knowledge Q&A for Competitive Exams (Download PDF)
Answers & Solutions:
1) Answer (A)
I : $\sqrt[3]{512}\times\sqrt{256}>\sqrt[3]{343}\times\sqrt{289}$
L.H.S. = $8\times16=128$
R.H.S. = $7\times17=119$
Thus, $128>119$, which is correct.
II : $\sqrt{121}+\sqrt[3]{1331}>\sqrt[3]{125}\times\sqrt{25}$
L.H.S. = $11+11=22$
R.H.S. = $5\times5=25$
Thus, $22<25$
$\therefore$ Only I is correct.
=> Ans – (A)
2) Answer (C)
Terms : $\sqrt{2},\sqrt[3]{2},\sqrt{4},\sqrt[3]{5}$
Here, $\sqrt2<2$ , $\sqrt[3]2<2$ and $\sqrt[3]5<2$
But, $\sqrt4=2$
Thus, $\sqrt4$ is the largest.
=> Ans – (C)
3) Answer (A)
Expression : $\sqrt{{2^{6}}+15^2}$
= $\sqrt{64+225}$
= $\sqrt{289}=17$
=> Ans – (A)
4) Answer (A)
Cost price of watch = Rs. 450
Price after 1st discount of 20% = $450-(\frac{20}{100}\times450)=Rs.$ $360$
Selling Price after 2nd discount of 5% = $360-(\frac{5}{100}\times360)=Rs.$ $342$
=> Ans – (A)
5) Answer (C)
6) Answer (A)
Expression : $\sqrt[3]{729}\times\sqrt{16}+\sqrt{676}+\sqrt{169}$
= $(9\times4)+26+13$
= $36+39=75$
=> Ans – (A)
7) Answer (B)
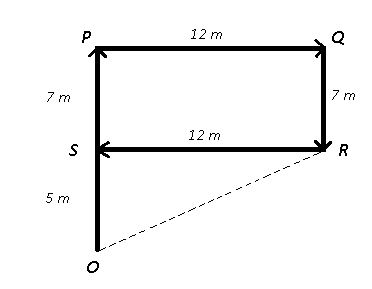
Let Manoj start from point O and walks 12 metres towards north to reach P. Then turns right and walk another 12 metres eastwards to reach Q. Then turn right and walks for 7 metres southwards to reach college R. He again turns to his right and walks for 12 metres.
Thus, $(OR)^2=(OS)^2+(SR)^2$
=> $(OR)^2=(5)^2+(12)^2$
=> $(OR)^2=25+144=169$
=> $OR=\sqrt{169}=13$ m
=> Ans – (B)
8) Answer (D)
I : $\sqrt{324}+\sqrt{3.24}+\sqrt{0.0324} = 19.98$
L.H.S. = $18+1.8+0.18=19.98=$ R.H.S.
II : $\sqrt{129+\sqrt{121}+\sqrt{361}+\sqrt{100}}=13$
L.H.S. = $\sqrt{129+11+19+10}=\sqrt{169}=13=$ R.H.S.
Thus, both I and II are correct.
=> Ans – (D)
9) Answer (B)
Expression : $2\sqrt[3]{243}+3\sqrt[3]{9}-\sqrt[3]{1125}$
= $2\sqrt[3]{27\times9}+3\sqrt[3]{9}-\sqrt[3]{125\times9}$
= $6\sqrt[3]9+3\sqrt[3]9-5\sqrt[3]9$
= $4\sqrt[3]9$
=> Ans – (B)
10) Answer (B)
Given : $x=\frac{\sqrt{5}+1}{\sqrt{5}-1}$ and $y=\frac{\sqrt{5}-1}{\sqrt{5}+1}$
To find : $x-y=?$
Solution = $(\frac{\sqrt{5}+1}{\sqrt{5}-1})-(\frac{\sqrt{5}-1}{\sqrt{5}+1})$
= $\frac{(\sqrt5+1)^2-(\sqrt5-1)^2}{(\sqrt5-1)(\sqrt5+1)}$
= $\frac{(6+2\sqrt5)-(6-2\sqrt5)}{(5-1)}$
= $\frac{4\sqrt5}{4}=\sqrt5$
=> Ans – (B)
11) Answer (A)
Given : $x = 4 + \sqrt{15}$ ————-(i)
=> $\frac{1}{x} = \frac{1}{4 + \sqrt{15}}$
=> $\frac{1}{x} = \frac{1}{4 + \sqrt{15}}\times(\frac{4-\sqrt{15}}{4-\sqrt{15}})$
=> $\frac{1}{x}=\frac{4-\sqrt{15}}{(16-15)}=4-\sqrt{15}$ ————-(ii)
To find : $[x^2 + (\frac{1}{x^2})]$
= $(x+\frac{1}{x})^2-2(x)(\frac{1}{x})$
Substituting values from equations (i) and (ii), we get :
= $[(4+\sqrt{15})+(4-\sqrt{15})]^2-2$
= $(8)^2-2=64-2=62$
=> Ans – (A)
12) Answer (C)
Expression : $p=\sqrt{72-\sqrt{72-\sqrt{72-\sqrt{72-……\infty}}}}$
=> $p=\sqrt{72-p}$
Squaring both sides, we get :
=> $p^2=72-p$
=> $p^2+p-72=0$
=> $p^2+9p-8p-72=0$
=> $p(p+9)-8(p+9)=0$
=> $(p+9)(p-8)=0$
=> $p=-9,8$
But $p$ cannot be negative, thus $p=8$
To find : $2p^2+1$
= $2(8)^2+1=128+1=129$
=> Ans – (C)
13) Answer (A)
Expression : $4^x= \sqrt[7]{1024}$
=> $4^x=\sqrt[7]{2^{10}}$
=> $4^x=\sqrt[7]{4^5}$
=> $4^x=4^{\frac{5}{7}}$
=> $x=\frac{5}{7}$
=> Ans – (A)
14) Answer (C)
Expression : $\sqrt[3]{512}+\sqrt{169}+\sqrt[3]{216}+\sqrt{225}$
= $\sqrt[3]{8\times8\times8}+13+\sqrt[3]{6\times6\times6}+15$
= $8+13+6+15=42$
=> Ans – (C)
15) Answer (C)
Given : $x=\frac{4}{2\sqrt{3}+3\sqrt{2}}$
Rationalizing the denominator, we get :
=> $x=\frac{4}{2\sqrt{3}+3\sqrt{2}}\times\frac{(2\sqrt3-3\sqrt2)}{(2\sqrt3-3\sqrt2)}$
=> $x=\frac{4(2\sqrt3-3\sqrt2)}{(12-18)}=\frac{2(3\sqrt2-2\sqrt3)}{3}$ ———(i)
Now, $\frac{1}{x}=\frac{3}{2(3\sqrt2-2\sqrt3)}\times\frac{(3\sqrt2+2\sqrt3)}{(3\sqrt2+2\sqrt3)}$
=> $\frac{1}{x}=\frac{3(3\sqrt2+2\sqrt3)}{2(18-12)}$
=> $\frac{1}{x}=\frac{3\sqrt2+2\sqrt3}{4}$ ————-(ii)
Adding equations (i) and (ii), we get :
=> $x+\frac{1}{x}=(\frac{2(3\sqrt2-2\sqrt3)}{3})+(\frac{3\sqrt2+2\sqrt3}{4})$
= $\frac{8(3\sqrt2-2\sqrt3)+3(3\sqrt2+2\sqrt3)}{12}$
= $\frac{24\sqrt2-16\sqrt3+9\sqrt2+6\sqrt3}{12}$
= $\frac{33\sqrt2-10\sqrt3}{12}$
= $\frac{-(10\sqrt3-33\sqrt2)}{12}$
=> Ans – (C)
16) Answer (C)
I : $(\sqrt{11}+\sqrt{2})>(\sqrt{8}+\sqrt{5})$
Squaring both sides, we get :
L.H.S. = $(\sqrt{11}+\sqrt2)^2=(11+2+2\sqrt{22})=13+2\sqrt{22}$
R.H.S. = $(\sqrt{8}+\sqrt5)^2=(8+5+2\sqrt{40})=13+2\sqrt{40}$
$\because$ $\sqrt{22}<\sqrt{40}$, then L.H.S. < R.H.S.
II : $(\sqrt{10}+\sqrt{3})>(\sqrt{7}+\sqrt{6})$
Squaring both sides, we get :
L.H.S. = $(\sqrt{10}+\sqrt3)^2=(10+3+2\sqrt{30})=13+2\sqrt{30}$
R.H.S. = $(\sqrt{7}+\sqrt6)^2=(7+6+2\sqrt{42})=13+2\sqrt{42}$
$\because$ $\sqrt{30}<\sqrt{42}$, then L.H.S. < R.H.S.
Thus, neither I nor II is correct.
=> Ans – (C)
17) Answer (C)
Given : $p+\frac{1}{p}=\sqrt{10}$
Squaring both sides, we get :
=> $(p+\frac{1}{p})^2=(\sqrt{10})^2$
=> $p^2+\frac{1}{p^2}+2(p)(\frac{1}{p})=10$
=> $p^2+\frac{1}{p^2}=10-2=8$
Again squaring both sides, we get :
=> $(p^2+\frac{1}{p^2})^2=(8)^2$
=> $p^4+\frac{1}{p^4}+2(p^2)(\frac{1}{p^2})=64$
=> $p^4+\frac{1}{p^4}=64-2=62$
=> Ans – (C)
18) Answer (C)
Given : $z=6-2\sqrt3$ —————–(i)
To find : $(\sqrt{z}-\frac{1}{\sqrt{z}})^2$
= $(\frac{z-1}{\sqrt{z}})^2=\frac{(z-1)^2}{z}$ ————(ii)
From equation (i), => $z-1=5-2\sqrt3$
Squaring both sides, we get :
=> $(z-1)^2=(5-2\sqrt3)^2$
=> $(z-1)^2=25+12-20\sqrt3=(37-20\sqrt3)$ ———-(iii)
Substituting values from equations (i) and (iii) in equation (ii),
=> $\frac{(z-1)^2}{z}=\frac{37-20\sqrt3}{6-2\sqrt3}$
Rationalizing the denominator, we get :
= $\frac{37-20\sqrt3}{6-2\sqrt3}\times\frac{(6+2\sqrt3)}{(6+2\sqrt3)}$
= $\frac{37(6+2\sqrt3)-20\sqrt3(6+2\sqrt3)}{36-12}$
= $\frac{222+74\sqrt3-120\sqrt3-120}{24}$
= $\frac{102-46\sqrt3}{24}$
=> Ans – (C)
19) Answer (A)
Expression : $[25+4\sqrt{39}]$
= $[25+2\sqrt{4\times39}]=[25+2\sqrt{156}]$
= $13+12+2\sqrt{13\times12}$
= $(13)^2+(12)^2+2\sqrt{13\times12}$
Now, we know that $a^2+b^2+2ab=(a+b)^2$
= $(\sqrt{13}+\sqrt{12})^2$
Thus, square root is = $\sqrt{13}+\sqrt{12}$
= $\sqrt13+2\sqrt3$
=> Ans – (A)
20) Answer (D)
Expression : $x=\sqrt{15\sqrt{15\sqrt{15\sqrt{15\sqrt{15….\infty}}}}}$
=> $x=\sqrt{15x}$
Squaring both sides, we get :
=> $x^2=15x$
=> $x=15$
To find : $x^2+4$
= $(15)^2+4=225+4=229$
=> Ans – (D)





