Simple Interest and Compound Interest Questions for RRB NTPC Set-2 PDF
Download RRB NTPC Simple & Compound Interest Questions and Answers PDF. Top 25 RRB NTPC Maths questions based on asked questions in previous exam papers very important for the Railway NTPC exam.
Download Simple and Compound Interest Questions for RRB NTPC Set-2 PDF
20 RRB NTPC Mocks – Just Rs. 149
RRB NTPC Previous Papers [Download PDF]
Question 1: In what time would the simple interest on a certain sum be 0.125 times the principal at 10% per annum ?
a) $1\frac{1}{4}$ years
b) $1\frac{3}{4}$ years
c) $2\frac{1}{4}$ years
d) $2\frac{3}{4}$ years
e) None of these
Question 2: How much will a sum of 12,0007 deposited at a rate of 9% per annum (simple interest) for 13 years amount to ?
a) 14,040
b) 20,650
c) 13,404
d) 27,800
e) 26,040
Instructions
Directions for the next five questions: Study the following table carefully to answer the questions.
Rate of interest (pcpa) offered by five companies on deposits under different schemes
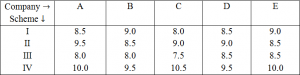
Question 3: Mr. X deposited an amount in Scheme II with company C for two years. After that he withdrew the amount and reinvested only the principal amount in scheme IV of Company B for two years. Total amount of simple interest accrued from the two schemes is Rs. 14800. What was the principal amount?
a) Rs. 48000
b) Rs. 42000
c) Rs. 40000
d) Can’t be determined
e) None of these
Question 4: Abishek invested an amount of Rs. 45000 for two years with company B under scheme III, Which offers compound interest, Jeevan invested an equal amount for two years with company C under Scheme IV, which offer simple Interest. Who earned more interest and how much?
a) Abhishek, Rs. 1875
b) Jeevan, Rs. 1875
c) Abhishek, Rs. 1962
d) Jeevan, Rs. 1962
e) None of these
Question 5: Mr. Lal invested Rs. 30000 in company A under Scheme II, which offers simple interest and Rs. 48000 in Company D under Scheme II, which offers compound interest. What will be the total amount of interest earned by Mr Lal in two years?
a) Rs. 14728.80
b) Rs. 17428.50
c) Rs. 14827.70
d) Rs. 16728.20
e) None of these
Question 6: The compound interest accured on an amount of Rs.22, 000 at the end of two years is Rs.5, 596.8. What would be the simple interest accrued on the same amount at the same rate in the same period?
a) Rs.5,420
b) Rs.5,360
c) Rs.5,280
d) Rs.5,140
e) None of these
Question 7: The simple interest accrued on an amount of Rs. 22,500 at the end of four years is Rs.10,800. What would be the compound interest accrued on the same amount at the same rate of interest at the end of two years?
a) Rs. 16, 908
b) Rs. 5, 724
c) Rs. 28, 224
d) Rs. 8, 586
e) None of these
Question 8: The simple interest accrued on a certain principal is Rs 35,672 in seven years at the rate of 8 pcpa. What would be the compound interest accrued on that principal at the rate of 2 pcpa in 2 years?
a) Rs 2573.48
b) Rs 2564.86
c) Rs 2753.86
d) Rs 2654.48
e) None of these
Question 9: The simple interest accrued on an amount of Rs. 22,500 at the end of four years is Rs.10,800. What would be the compound interest accrued on the same amount at the same rate of interest at the end of two years?
a) Rs. 16, 908
b) Rs. 5, 724
c) Rs. 28, 224
d) Rs. 8, 586
e) None of these
RRB NTPC Previous Papers Download PDF
RRB JE PREVIOUS PAPERS DOWNLOAD
Question 10: A sum of Rs16800 is divided into two parts. One part is lent at the simple interest of 6% per annum and the other at 8% per annum. After 2 years total sum received is Rs19000. The sum lent at 6% of simple interest is
a) ` 12200
b) ` 12000
c) ` 11000
d) ` 10000
e) None of these
Question 11: Rs.X triples itself in 6 years at simple interest of R%. A person invested Rs.X at R% per annum compound interest compounded annually. If the amount received after 3 years is Rs.38394, then find the simple interest received on Rs.X at R% per annum for 4 years.
a) Rs.21540
b) Rs.22460
c) Rs.21600
d) Rs.20480
e) None of these
Question 12: Raman deposited Rs.P in a scheme for 3 year at the rate of 10% per annum simple interest. Total amount obtained after 3 years with Rs. 1000 was deposited in a bank which offered 20% per annum compound interest. After 2 years compound interest obtained from the bank was Rs. 6160. Then what is the value of P(in Rs.)?
a) Rs. 15000
b) Rs. 12000
c) Rs. 10000
d) Rs. 9000
e) Rs. 18000
Instructions
Question 13: The difference between Compound interest and Simple interest for 2 years for Principle Rs 32000 is Rs 720. What is the rate of interest ?
a) 14%
b) 15%
c) 12%
d) 10%
e) 20%
Question 14: A sum of money at compound interest yields an amount of Rs 1,25,000 in 3 years and Rs 1,95,312.5 in 5 years. What is the rate of interest per annum ?
a) 15%
b) 20%
c) 25%
d) 30%
e) 10%
Question 15: Ajay invested a certain amount of money in simple interest for a period of 3 years at 17% simple interest and gets an interest of 2856. If he invested the total amount received in a scheme which offered compound interest at a rate which is 3% more than the earlier rate for a period of 2 years. Then find the total interest he received from the scheme at the end of 2 years (approximately)?
a) 3756
b) 3607
c) 3475
d) 4500
e) 3721
18000+ Questions – Free SSC Study Material
Download General Science Notes PDF
Answers & Solutions:
1) Answer (A)
2) Answer (E)
3) Answer (C)
Let principal amount be Rs. x.
(x×9×2)/100 + (x×9.5×2)/100 = 14800
or (0.18+0.19) = 14800
X = 14800/0.37 = Rs. 40000
4) Answer (D)
Interest earned by Abhishek = 45000 × (1+ 8/100)^2- 45000
= 45000 × 27/25 × 27/25 = 45000
= 52488 – 45000 = 7488
Interest earned by Jeevan = (45000×10.5×2)/100 = 9450
Required difference = 9450 – 7488 = 1962
Hence, Jeevan earned Rs. 1962 more.
5) Answer (A)
(30000×9.5×2)/100 + (48000× 109/100× 109/100- 48000) = 5700 + (57028.8 – 48000)
= 5700 + 9028.8 = Rs. 14728.80
6) Answer (C)
Let the rate of interest be R% per annum.
CI = P [(1 + $\frac{R}{100})^{T}$ -1]
=5596.8
= 22000 [(1 + $\frac{R}{100})^{2}$-1]
$\frac{5596.8}{22000}$ = (1+ $\frac{R}{100})^{2}$ -1
(1 + $\frac{R}{100})^{2}$ = 1 + $\frac{5596.8}{22000}$
(1 + $\frac{R}{100})^{2}$ = $\frac{22000 + 5596.8}{22000}$ = $\frac{27596.8}{22000}$
(1+$\frac{R}{100})^{2}$ = $\frac{275968}{220000}$ = $\frac{12544}{10000}$
$\frac{R}{100}$ = $\sqrt{\frac{12544}{10000}}$ – 1 = $\frac{112}{100}$
= $\frac{R}{100}$ = $\frac{112}{100}$ – 1 = $\frac{112 – 100}{100}$ = $\frac{12}{100}$
R=12
SI = $\frac{Principal × Time × Rate}{100}$ = $\frac{22000 × 2 × 100}{100}$ = Rs.5280
7) Answer (B)
Let the rate of interest be r
Simple Interest = $\frac{P t r}{100}$
10800 = $\frac{22500}{100}$ x 4 x r
r = $\frac{10800}{22500}$ x $\frac{100}{4}$ = 12%
Compound Interest = 22500(1 + $\frac{12}{100}$)2 – 22500
= 22500 x $\frac{112}{100}$ x $\frac{112}{100}$ – 22500
= 28224 – 22500
= 5724
8) Answer (A)
PTR/100 = 35672 => P = 35672 * 100 / (7*8) = 63700
Compound interest in 2 years = P(1+r/100)^2 – P = 63700(1+1/50)^2 – 63700 = 2573.48
9) Answer (B)
Let the rate of interest be r
Simple Interest = $\frac{P t r}{100}$
10800 = $\frac{22500}{100}$ x 4 x r
r = $\frac{10800}{22500}$ x $\frac{100}{4}$ = 12%
Compound Interest = 22500(1 + $\frac{12}{100}$)2 – 22500
= 22500 x $\frac{112}{100}$ x $\frac{112}{100}$ – 22500
= 28224 – 22500
= 5724
10) Answer (A)
Let x be the amount lent for 6%
16800 – x is the amount lent for 8%
$\frac{2×6}{100}$ + $\frac{2(16800-x)8}{100}$ + 16800 = 19000
x = 12200
11) Answer (C)
Given, Principal = Rs.X
Rate of interest = R%
Time duration = 6 years
Amount after 6 years = Rs.3X
Simple Interest after 6 years = Rs.3X – Rs.X = Rs.2X
$\dfrac{X\times R\times6}{100} = 2X$
$R = \dfrac{100}{3}$% $= \dfrac{1}{3}$
Amount received after 3 years at compound interest $= X \times \dfrac{4}{3}\times\dfrac{4}{3}\times\dfrac{4}{3} = 2.37X$
Given, $2.37X = 38394$
=> $X = 16200$
Hence, Principal = Rs.16200
Simple Interest at $\dfrac{1}{3}$ in 4 years = $4\times\dfrac{1}{3}\times16200 = Rs.21600$
12) Answer (C)
Raman deposited Rs.P in a scheme for 3 year at the rate of 10% per annual simple interest.
So interest obtained from that scheme after 3 years = $\text{Deposited amount}\times \text{Rate of interest}\times \text{Time}$
= $P\times 10$%$\times 3$
= $30P$%
= $\dfrac{30P}{100}$
= .3P
Total amount obtained after 3 years = Interest + Deposited amount
= .3P + P
= 1.3P
Now as per question, we have to add Rs.1000 in that amount.
So it will be (1.3P + 1000). Eq.(1)
Now it will be deposited in bank at the rate of 20% per annual compound interest for 2 years. Then compound interest after 2 years = Rs. 6160 Eq.(2)
Formula for compound interest (CI) = $\text{Principal amount}[(1 + \dfrac{\text{Rate of interest}}{100})^{\text{Time}} – 1]$
Put the values from Eq.(1) and Eq.(2) in the formula.
$6160 = (1.3P + 1000)[(1 + \dfrac{20}{100})^{2} – 1]$
$6160 = (1.3P + 1000)[(\dfrac{120}{100})^{2} – 1]$
$6160 = (1.3P + 1000)[(\dfrac{6}{5})^{2} – 1]$
$6160 = (1.3P + 1000)[(\dfrac{36}{25}) – 1]$
$6160 = (1.3P + 1000)[(\dfrac{36-25}{25})]$
$6160 = (1.3P + 1000)[(\dfrac{11}{25})]$
$6160 = (1.3P + 1000)[(\dfrac{11}{25})]$
$6160\times\dfrac{25}{11} = (1.3P + 1000)$
$560\times25 = (1.3P + 1000)$
14000 = (1.3P + 1000)
14000 – 1000 = 1.3P
1.3P = 13000
$P = \dfrac{13000}{1.3}$
$P = \dfrac{130000}{13}$
P = 10000.
Hence, option c is the correct answer.
13) Answer (B)
We have CI=$P(1+\dfrac{R}{100})^{2}-P$
CI=$P((1+\dfrac{R}{100})^{2}-1)$
CI=$32000((1+\dfrac{R}{100})^{2}-1)$
let R/100 =r
CI=$32000((1+r)^{2}-1)$
CI=$32000*(r^{2}+2r)$
SI=$32000*2*R/100$
SI=64000r
$32000*(r^{2}+2r)-64000r$=720
$3200(r^{2}+2r)-6400r$=72
$3200r^{2}+6400r-6400r$=72
$r^{2}$=72/3200
$r^{2}$=0.0225
r=0.15
R=0.15*100
R=15%
14) Answer (C)
A=$P(1+\dfrac{R}{100})^{3}$
125000=$P(1+\dfrac{R}{100})^{3}$
195312.5=$P(1+\dfrac{R}{100})^{5}$
$(1+\dfrac{R}{100})^{2}$=1.5625
$1+(R/100)$=1.25
R/100 =0.25
R=25%
15) Answer (E)
As per the given question,
$\frac{P \times 3 \times 17}{100} = 2856$
$P = 5600$
He invested the total amount i.e (5600 + 2856) 8456 in a scheme for two years at 20% (17% +3%).
For the first year, the interest accumulated will be 20% of 8456 i.e 1691.2
The total amount will be 8456 + 1691.2 = 10147.2
For the second year, the interest accumulated will be 20% of 10147.2 i.e 2029.44
Total interest for two years will be 1691.2 + 2029.44 = 3720.64(approximately)
Hence, option E is the correct answer.
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Simple & Compound Interest questions for RRB NTPC Exam will be highly useful for your preparation.





