Selection Criteria Questions for MAH-CET
Here you can download a free Selection Criteria questions PDF with answers for MAH MBA CET 2022 by Cracku. These are some tricky questions in the MAH MBA CET 2022 exam that you need to find the Selection criteria of answers for the given questions. These questions will help you to make practice and solve the Selection Criteria questions in the MAH MBA CET exam. Utilize this best PDF practice set which is included answers in detail. Click on the below link to download the Selection Criteria MCQ PDF for MBA-CET 2022 for free.
Download Selection Criteria Questions for MAH-CET
Enroll to MAH-CET 2022 Crash Course
Instructions
In the table below the check marks indicate all languages spoken by five people: Paula, Quentin, Robert, Sally and Terence. For example, Paula speaks only Chinese and English.

These five people form three teams, Team 1, Team 2 and Team 3. Each team has either 2 or 3 members. A team is said to speak a particular language if at least one of its members speak that language.
The following facts are known.
(1) Each team speaks exactly four languages and has the same number of members.
(2) English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team.
(3) None of the teams include both Quentin and Robert.
(4) Paula and Sally are together in exactly two teams.
(5) Robert is in Team 1 and Quentin is in Team 3.
Question 1: Apart from Chinese and English, which languages are spoken by Team 1?
a) Arabic and French
b) Basque and French
c) Arabic and Basque
d) Basque and Dutch
1) Answer (A)
Solution:
From statement 1 and 2,Each team speaks exactly four languages. English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team, multiple options are possible.
In the following tables: A, B, C can be any team among Team 1,Team 2,Team 3.
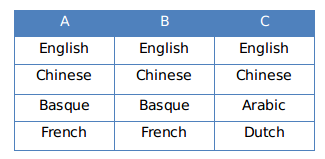

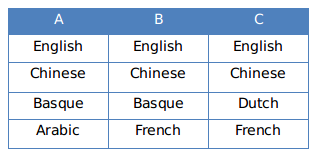
From the data given in the question, the person who speaks Arabic also speaks French. Thus the only option possible is ‘Table 2’.
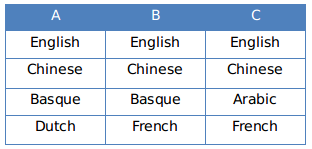
According to statement 4, “Paula and Sally are together in exactly two teams.”
Sally knows Basque, thus, she will be in group A and B, with Paula.
According to statement 5, Robert(Arabic) is in Team 1 and Quentin(Dutch) is in Team 3.
Thus, Group C is Team 1 and Group A is Team 3.
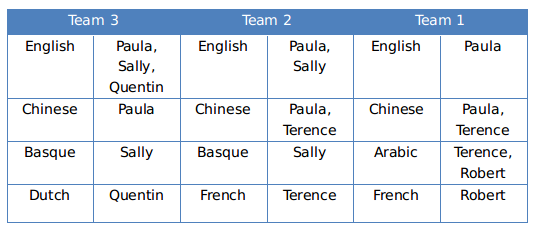
From the table, the correct option is A.
Question 2: Who among the five people is a member of all teams?
a) Terence
b) Sally
c) Paula
d) No one
2) Answer (C)
Solution:
From statement 1 and 2,Each team speaks exactly four languages. English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team, multiple options are possible.
In the following tables: A, B, C can be any team among Team 1,Team 2,Team 3.



From the data given in the question, the person who speaks Arabic also speaks French. Thus the only option possible is ‘Table 2’.

According to statement 4, “Paula and Sally are together in exactly two teams.”
Sally knows Basque, thus, she will be in group A and B, with Paula.
According to statement 5, Robert(Arabic) is in Team 1 and Quentin(Dutch) is in Team 3.
Thus, Group C is Team 1 and Group A is Team 3.

From the table, the correct option is C.
Question 3: Who among the following four people is a part of exactly two teams?
a) Paula
b) Quentin
c) Sally
d) Robert
3) Answer (C)
Solution:
From statement 1 and 2,Each team speaks exactly four languages. English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team, multiple options are possible.
In the following tables: A, B, C can be any team among Team 1,Team 2,Team 3.



From the data given in the question, the person who speaks Arabic also speaks French. Thus the only option possible is ‘Table 2’.

According to statement 4, “Paula and Sally are together in exactly two teams.”
Sally knows Basque, thus, she will be in group A and B, with Paula.
According to statement 5, Robert(Arabic) is in Team 1 and Quentin(Dutch) is in Team 3.
Thus, Group C is Team 1 and Group A is Team 3.

From the table, the correct option is C.
Question 4: Who among the following four is not a member of Team 2?
a) Paula
b) Terence
c) Quentin
d) Sally
4) Answer (C)
Solution:
From statement 1 and 2,Each team speaks exactly four languages. English and Chinese are spoken by all three teams, Basque and French by exactly two teams and the other languages by exactly one team, multiple options are possible.
In the following tables: A, B, C can be any team among Team 1,Team 2,Team 3.



From the data given in the question, the person who speaks Arabic also speaks French. Thus the only option possible is ‘Table 2’.

According to statement 4, “Paula and Sally are together in exactly two teams.”
Sally knows Basque, thus, she will be in group A and B, with Paula.
According to statement 5, Robert(Arabic) is in Team 1 and Quentin(Dutch) is in Team 3.
Thus, Group C is Team 1 and Group A is Team 3.

From the table, the correct option is C.
Instructions
K, L, M, N, P, Q, R, S, U and W are the only ten members in a department. There is a proposal to form a team from within the members of the department, subject to the following conditions:
- A team must include exactly one among P,R and S.
- A team must include either M or Q, but not both.
- If a team includes K, then it must also include L, and vice versa.
- If a team includes one among S, U and W, then it should also include the other two.
- L and N cannot be members of the same team.
- L and U cannot be members of the same team.
The size of a team is defined as the number of members in the team.
Question 5: Who cannot be a member of a team of size 3?
a) L
b) M
c) N
d) P
e) Q
5) Answer (A)
Solution:
If L is in the team, the team should include K also. The team should have one among P, R and S and one among M and Q.
So, the team size cannot be 3 if L is in the team.
Take Free MAH-CET mock tests here
Enroll to 5 MAH CET Latest Mocks For Just Rs. 299
Question 6: Who can be a member of a team of size 5?
a) K
b) L
c) M
d) P
e) R
6) Answer (C)
Solution:
Out of P, R and S only 1 can be in the team. If S is there, U and W will also be there. So, P and R should not be in the team for its size to be maximum.
Out of M and Q, only 1 can be there.
If L is there in the team, N and U cannot be in the team.
If L is not there in the team, then K is also not there in the team but N and U can be in the team.
So, the maximum team size is 5 consisting of S, U, W, (M or Q), N.
So, M can be a member of team size 5.
Question 7: What would be the size of the largest possible team?
a) 8
b) 7
c) 6
d) 5
e) cannot be determined
7) Answer (D)
Solution:
Out of P, R and S only 1 can be in the team. If S is there, U and W will also be there. So, P and R should not be in the team for its size to be maximum.
Out of M and Q, only 1 can be there.
If L is there in the team, N and U cannot be in the team.
If L is not there in the team, then K is also not there in the team but N and U can be in the team.
So, the maximum team size is 5 consisting of S, U, W, (M or Q), N.
Question 8: In how many ways a team can be constituted so that the team includes N?
a) 2
b) 3
c) 4
d) 5
e) 6
8) Answer (E)
Solution:
Since N is in the team, L and K cannot be in the team.
The team can have one of M and Q. So, 2 ways of selection.
If the team has S, then it should have U and W as well.
If the team has no S, then it should have one of P or R.
So, the number of ways of forming the team is 2*(1+2) = 6 ways
Question 9: What could be the size of a team that includes K?
a) 2 or 3
b) 2 or 4
c) 3 or 4
d) Only 2
e) Only 4
9) Answer (E)
Solution:
A team which has K should have L also.
Since L is there in the team, N and U should not be there in the team. Since U is not there in the team, S and W should not be there in the team.
So, the team will have K, L, one of P and R and one of M or Q.
So, the team size will be 4.





