RRB NTPC Previous Year Maths Questions PDF
Download RRB NTPC Previous year Maths Questions and Answers PDF. Top 15 RRB NTPC Maths questions based on asked questions in previous exam papers very important for the Railway NTPC exam.
Download RRB NTPC Previous Year Maths Questions PDF
Take a free mock test for RRB NTPC
Download RRB NTPC Previous Papers PDF
Question 1: In $\triangle$PQR, S and T are the mid points of sides PQ and PR respectively. If $\angle$QPR = $45^{0}$ and $\angle$PRQ = $55^{0}$, then what is the value (in degrees) of $\angle$QST ?
a) 80
b) 85
c) 90
d) 100
Question 2: If $(x-\frac{1}{x})=3$, then what is the value of $(x^{3}-\frac{1}{x^{3}})$ ?
a) 36
b) 21
c) 9
d) 27
Question 3: Amit goes to his office by car at the speed of 80 km\hr and reaches 15 minutes earlier. If he goes at the speed 60 km/hr, he reaches 15 minutes late. What will be the speed (in km/hr) of the car to reach on time ?
a) $66\frac{2}{7}$
b) $67\frac{4}{7}$
c) $68\frac{4}{7}$
d) $69\frac{4}{7}$
RRB NTPC Previous Papers [Download PDF]
Question 4: Which of the following fractions does not lie between $\frac{5}{6}$ and $\frac{8}{15}$ ?
a) $\frac{2}{3}$
b) $\frac{3}{4}$
c) $\frac{4}{5}$
d) $\frac{6}{7}$
Question 5: The sum of present ages of 4 children who were born in an interval of 4 years is 78 years. What is the age of the eldest person?
a) 27 years
b) 12 years
c) 11 years
d) 25 years
Question 6: The ratio of the ages of A, B and C is 5 : 8 : 9. If the sum of the ages of A and C is 56 years, the age of B will be
a) 12 years
b) 23 years
c) 21 years
d) 32 years
Question 7: The sum of the ages of husband and wife at present is 100. Ten years ago the ratio of their ages was 9:7. What is the age of the husband?
a) 45 years
b) 55 years
c) 65 years
d) 40 years
Question 8: If $l^{3} + m^{3}$ = -218 and $lm = -35$ , then what is the value of $l + m$?
a) -6
b) -2
c) -4
d) -5
Question 9: If $\large\frac{p}{q}+\frac{q}{p}$ $=-1$, then the value of $p^{3}-q^{3}$ is
a) 64
b) 27
c) 100
d) 0
Download General Science Notes PDF
Question 10: If $1^{2}+2^{2}+3^{2}+……..+n^{2}$ = $\frac{n(n+1)(2n+1)}{6}$, then $1^{2}+3^{2}+5^{2}+……..+29^{2}$ is equal to:
a) 4385
b) 4395
c) 4495
d) 4485
Question 11: Find the number of prime factors of 14560
a) 3
b) 4
c) 5
d) 6
Download General Science Notes PDF
Question 12: In a class, there are 40 students. Some of them passed the examination and others failed. Raman’s rank among the student who have passed is 13 th from top and 17 th from bottom. How many students have failed?
a) 11
b) 10
c) 9
d) Cannot be determined
Question 13: What is the square root of $\frac{(3-2\sqrt2)}{(3+2\sqrt2)}$ ?
a) $3-2\sqrt2$
b) $3+2\sqrt2$
c) $1$
d) $17$
Daily Free RRB Online Tests for RRB Exams
Question 14: The number of diagonals of a regular polygon is 20. What is the ratio of an exterior angle to the interior angle of the regular polygon ?
a) 2:5
b) 1:3
c) 2:7
d) 1:4
Question 15: Find the area(in sq.cm) of the sector subtending 72° at the centre of a circle with a radius of 35cm ?
a) 690
b) 734
c) 770
d) 792
Download Current Affairs Questions & Answers PDF
Answers & Solutions:
1) Answer (D)
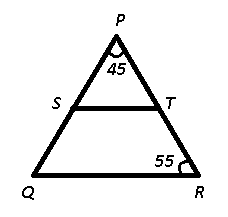
Given : $\angle$QPR = $45^\circ$ and $\angle$PRQ = $55^\circ$
To find : $\angle$QST = ?
Solution : In triangle, PQR
=> $\angle P+\angle Q+\angle R=180^\circ$
=> $45^\circ+55^\circ+\angle Q=180^\circ$
=> $\angle Q=180^\circ-100^\circ=80^\circ$
Now, since ST divides PQ and PR equally, thus ST is parallel to QR.
$\therefore$ Angles on the same side of transversal are supplementary, => $\angle PQR+\angle QST=180^\circ$
=> $\angle QST=180^\circ-80^\circ=100^\circ$
=> Ans – (D)
2) Answer (A)
Given : $(x-\frac{1}{x})=3$ ———-(i)
Cubing both sides, we get :
=> $(x-\frac{1}{x})^3=(3)^3$
=> $x^3-\frac{1}{x^3}-3(x)(\frac{1}{x})(x-\frac{1}{x})=27$
=> $x^3-\frac{1}{x^3}-3(1)(3)=27$
=> $(x^{3}-\frac{1}{x^{3}})=27+9=36$
=> Ans – (A)
3) Answer (C)
Let ideal time taken to reach on time = $t$ hours
Speed is inversely proportional to time
=> $\frac{80}{60}=\frac{t+\frac{1}{4}}{t-\frac{1}{4}}$
=> $80t-20=60t+15$
=> $80t-60t=20t=15+20$
=> $t=\frac{35}{20}=\frac{7}{4}$ hours
Thus, distance covered by going at 60 km/hr and reaching in $(\frac{7}{4}+\frac{1}{4}=2)$ hours = $60\times2=120$ km
$\therefore$ Ideal speed to reach on time = $\frac{120\times4}{7}=68\frac{4}{7}$ km/hr
=> Ans – (C)
4) Answer (D)
$\frac{5}{6}=0.83$ and $\frac{8}{15}=0.53$
(A) : $\frac{2}{3}=0.6$
(B) : $\frac{3}{4}=0.75$
(C) : $\frac{4}{5}=0.8$
(D) : $\frac{6}{7}=0.85$
Thus, $\frac{6}{7}$ does not lie between $\frac{5}{6}$ and $\frac{8}{15}$
=> Ans – (D)
5) Answer (A)
Taking x as the age of the youngest one,
x + (x + 5) + (x + 10) + (x + 15) = 78 years
4x + 30 = 78
x = 12 years. Hence, the age of the eldest one is (12 + 15 ) = 27 years
6) Answer (D)
Let the ages of A, B and C respectively be $5x,8x$ and $9x$ years.
According to ques, => $5x+9x=56$
=> $x=\frac{56}{14}=4$
$\therefore$ B’s age = $8\times4=32$ years
=> Ans – (D)
7) Answer (B)
Let husband’s age = $x$ years
=> Wife’s age = $(100 – x)$ years
According to ques,
=> $\frac{x – 10}{100 – x – 10} = \frac{9}{7}$
=> $\frac{x – 10}{90 – x} = \frac{9}{7}$
=> $7x – 70 = 810 – 9x$
=> $9x + 7x = 810 + 70 = 880$
=> $x = \frac{880}{16} = 55$ years
=> Ans – (B)
8) Answer (B)
Given, $l^{3} + m^{3}$ = -218 and $lm = -35$
$(l+m)^{3} = l^{3}+ m^{3} + 3lm(l+m)$
$(l+m)^{3} = -218 + 3(-35)(l+m)$
$(l+m)^{3} = -218 -105(l+m)$
we need to solve 3rd degree equation
so,without solving, by verification, we get $l+m = -2$,
so the answer is option B.
9) Answer (D)
Given,
$\large\frac{p}{q}+\frac{q}{p}$ $=-1$
$\large\frac{p^{2}+q^{2}}{pq}$ $ = -1$
$p^{2}+q^{2} = -pq$
$p^{2}+q^{2} + pq = 0$
We know $p^{3}-q^{3}={(p-q)}{(p^{2}+q^{2}}{+pq)} $
As $p^{2}-q^{2} + pq = 0$, therefore $p^{3}-q^{3}={(p-q)}{(p^{2}+q^{2}}{+pq)}=0$
10) Answer (C)
Let that fraction be $\frac{1}{f}$
Expression : $1^{2}+3^{2}+5^{2}+……..+29^{2}$
= $[1^{2}+2^{2}+3^{2}+4^{2}……..+28^{2}+29^{2}]$ $-[2^2+4^2+………+28^2]$
= $[1^{2}+2^{2}+3^{2}+4^{2}……..+28^{2}+29^{2}]$ $-(2^2)[1^2+2^2+3^2………+14^2]$
= $[\frac{29(29+1)(58+1)}{6}]-[4\times\frac{14(14+1)(28+1)}{6}]$
= $[\frac{29(30)(59)}{6}]-[4\times\frac{14(15)(29)}{6}]$
= $[29\times5\times59]-[4\times5\times7\times29]$
= $8555-4060=4495$
=> Ans – (C)
11) Answer (B)
We have to factorise the number into prime factors i.e
14560=$2^{5}*5*13*7$
There are 4 different prime factors namely 2,5,7 and 13.
12) Answer (A)
Total number of students = 40
Among the student who have passed, Raman’s rank from top = 13th
Raman’s rank from bottom = 17th
=> Total students who passed = $(13+17)-1=30-1=29$
$\therefore$ Number of students who have failed = $40-29=11$
=> Ans – (A)
13) Answer (A)
Given : $x=\frac{(3-2\sqrt2)}{(3+2\sqrt2)}$
To find : $\sqrt{x}$
Solution : rationalizing the denominator, we get
=> $\frac{(3-2\sqrt2)}{(3+2\sqrt2)}\times\frac{(3-2\sqrt2)}{(3-2\sqrt2)}$
= $\frac{(3-2\sqrt2)^2}{(3)^2-(2\sqrt2)^2}$
= $\frac{(3-2\sqrt2)^2}{9-8}$
=> $x=(3-2\sqrt2)^2$
Taking square root on both sides,
=> $\sqrt{x}=3-2\sqrt2$
=> Ans – (A)
14) Answer (B)
Number of diagonals of a regular polygon =n(n-3)/2
n(n-3)=40
$n^{2}-3n-40$=0
$n^{2}+5n-8n-40$=0
n(n+5)-8(n+5)=0
(n-8)(n+5)=0
n=8
Each interior angle of a regular polygon=(2n-4)90/n
Each exterior angle of a regular polygon=360/n
Ratio of exterior angle to interior angle=2/n-2
For n=8 we have 2/6=1:3
15) Answer (C)
We know that,
Area of sector of a circle = $\frac{x}{360}*\pi *r^{2}$
Where $x$ is the angle subtended at the centre and $r$ is the radius of the circle
Area =$\frac{72}{360}\times\pi \times35^{2}$ = 770 sq.cm
DOWNLOAD APP FOR RRB FREE MOCKS
We hope this Previous Year Maths Questions for RRB NTPC Exam will be highly useful for your Preparation.





