Ratio and Proportion Questions For SSC Stenographer PDF

SSC Stenographer Constable Ratio and Proportion Question and Answers download PDF based on previous year question paper of SSC Stenographer exam. 40 Very important Ratio and Proportion questions for Stenographer Constable.

RATIO AND PROPORTION QUESTIONS FOR SSC STENOGRAPHER PDF

10 Stenographer Mock Tests – Just Rs. 117

FREE SSC EXAM YOUTUBE VIDEOS

Download All Important SSC Stenographer Questions PDF (Topic-Wise)

SSC Stenographer Free Mock Test (Latest Pattern)

SSC Stenographer Previous Papers

Question 1: Three containers whose volumes are in the ratio of : 3 : 4 are full of mixture of spirit and water. In the 1st container, the ratio of spirit and water is 4: 1, in the 2nd container the ratio is 11 : 4 and in the 3rd container ratio is 7: 3. All the three mixture are mixed in a big container. The ratio of spirit and water in the resultant mixture is :

a) 4 : 9

b) 11 : 4

c) 5 : 10

d) 9 : 5

Question 2: The ratio between the ages of x and y at present is 3:4. Five years hence, the ratio of their ages will be 4:5; what is the present age of y in years ?

a) 15

b) 20

c) 25

d) 30

Question 3: An amount of money is to be distributed among P, Q and R in the ratio of 5:9:17 respectively. If the total of the shares of P and Q is Rs.7,000. What is R’s share in it

a) Rs.4,500

b) Rs.2,500

c) Rs.8,500

d) Rs.6,000

Question 4: Gold is 19 times as heavy as water and copper is 9 times as heavy as water. In what ratio should these be mixed to get an alloy 15 times as heavy as water ?

a) 1 : 1

b) 2 : 1

c) 1 : 2

d) 3 : 2

Question 5: The ages of x and y are in the ratio 3:1. Fifteen years hence, the ratio will be 2:1. The present ages (in years) are:

a) 30, 10

b) 45, 15

c) 21, 7

d) 60, 20

Download SSC Stenographer Syllabus PDF

SSC STENO FREE MOCK TEST

Question 6: In a school $\ \frac{1}{10}\ $of the boys are same in number as $\ \frac{1}{4}\ $of the girls and$\ \frac{5}{8}\ $of the girls are same in number as $\ \frac{1}{4}\ $of the boys. The ratio of the boys to girls in that school is

a) 2 : 1

b) 5 : 2

c) 4 : 3

d) 3 : 2

Question 7: The perimeter of a triangle and an equilateral triangle are same. Also, one of the sides of the rectangle is equal to the side of the triangle. The ratio of the areas of the rectangle and the triangle is

a) $\sqrt{3}\ $: 1

b) 1 :$\ \sqrt{3}$

c) 2: $\ \sqrt{3}$

d) 4 : $\ \sqrt{3}$

FREE SSC MATERIAL – 18000 FREE QUESTIONS

Instructions

The following pie-chart shows the market share of four companies S, T, U and V. Total market is worth Rs.72 crores. Study the pie-chart and answer the questions.

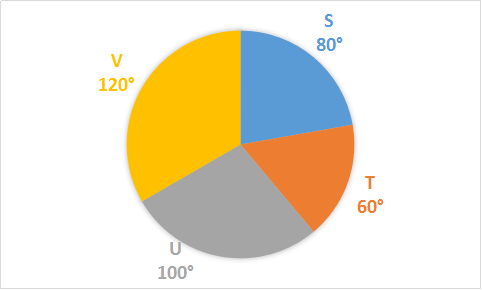
Question 8: The time required for a boy to travel along the external and internal boundaries of a circular path are in the ratio 20: 19. If the width of the path be 5 metres, the internal diameter is:

a) 195 metres

b) 192 metres

c) 180 metres

d) 190 metres

Question 9: If x, y are rational numbers and $\frac{5+\sqrt{11}}{3-2\sqrt{11}}$= x + y$\ \sqrt{11}$. The values of x and y are

a) x = $\ \frac{-14}{17}, y = \frac{-13}{26}$

b) x =$\ \frac{4}{13}, y = \frac{11}{17}$

c) x =$\ \frac{-27}{25}, y = \frac{-11}{37}$

d) x =$\ \frac{-37}{35}, y = \frac{-13}{35}$

Question 10: The three angles of a triangle are in the ratio 3 : 4 : 5. Then the angles respectively are:

a) $45^\circ,60^\circ, 75^\circ$

b) $60^\circ,45^\circ, 75^\circ$

c) $60^\circ,75^\circ, 45^\circ$

d) $75^\circ,60^\circ, 45^\circ$

Question 11: Radius of hemisphere is thrice than that of a sphere. What is the ratio of total surface area of hemisphere to that of sphere?

a) 27 : 8

b) 21 : 4

c) 27 : 4

d) 6 : 1

Question 12: Three bottles of equal capacity are containing a mixture of milk and water in ratio 2 : 1, 3 : 7 and 4 : 11 respectively. These three bottles are emptied
into a large bottle. What is the ratio of milk and water respectively in this large bottle?

a) 37 : 53

b) 37 : 90

c) 37 : 30

d) 7 : 30

Question 13: The ratio of the speed of P, Q and R is 10 : 12 : 15 respectively. What is the ratio of the time taken by P, Q and R respectively to cover the same distance?

a) 10 : 12 : 15

b) 15 : 12 : 10

c) 6 : 5 : 4

d) 4 : 5 : 6

Question 14: If the height of a given cone became thrice and the radius of the base remains the same. What is the ratio of the volume of the given cone and the volume of the second cone?

a) 1 : 3

b) 1 : 9

c) 1 : √3

d) 1 : 27

Question 15: In what ratio wheat at Rs 32/kg should be mixed with wheat at Rs 24/kg so that on selling the mixture at Rs 39/kg there is a profit of 30%?

a) 3 : 1

b) 2 : 3

c) 1 : 4

d) 2 : 5

SSC STENOGRAPHER PREVIOUS PAPERS

GK Questions and Answers PDF

Question 16: If 2A = 3B = 5C, then what is A : B : C?

a) 2 : 3 : 5

b) 5 : 3 : 2

c) 6 : 10 : 15

d) 15 : 10 : 6

Instructions

The given pie chart shows the expenditure (in degrees) incurred in making a book.

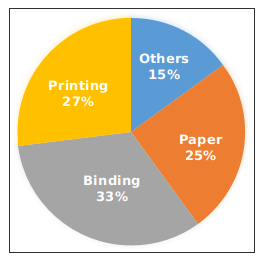
Question 17: In Others there are only two types of expenditures viz. Marketing and Distribution in ratio 3 : 2 respectively. What will be the central angle (in degrees) made by the sector of expenditure on Marketing?

a) 21.6

b) 32.4

c) 27

d) 36

Question 18: In ΔPQR, a line parallel to side QR cuts the side PQ and PR at points M and N respectively and point M divide PQ in the ratio of 1 : 2. If area of ΔPQR is 360 cm2, then what is the area (in cmb: of quadrilateral MNRQ?

a) 160

b) 320

c) 120

d) 96

Question 19: A cuboid of sides 5 cm, 10 cm and 20 cm are melted to form a new cube. What is the ratio between the total surface area of the cuboid and that of the cube?

a) 6 : 5

b) 7 : 6

c) 11 : 10

d) 9 : 7

Question 20: The ratio of curved surface area of two cones is 1 : 9 and the ratio of slant height of the two cones is 3 : 1. What is the ratio of the radius of the two cones?

a) 1 : 3

b) 1 : 9

c) 1 : 27

d) 1 : 1

Question 21: If 3P = 5Q = 15R, then what is P : Q : R?

a) 5 : 3 : 4

b) 5 : 3 : 1

c) 3 : 5 : 15

d) 15 : 5 : 3

Question 22: The ratio of two numbers is 5 : 11. If both numbers are increased by 10, the ratio becomes 7 : 13. What is the sum of the two numbers?

a) 80

b) 32

c) 48

d) 160

Instructions

The following pie chart shows the expenditure (in percentage) of five companies P, Q, R, S and T in the year 2016. Total Expenditure = 48 crores.

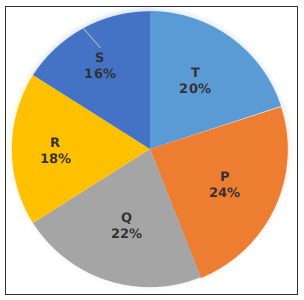
Question 23: What is the respective ratio between the total expenditure of company P, Q and S together to the total expenditure?

a) 31 : 60

b) 50 : 31

c) 60 : 31

d) 31 : 50

Question 24: The ratio of two numbers is 3 : 5. If both numbers are increased by 8, the ratio becomes 13 : 19. What is the sum of the two numbers?

a) 32

b) 48

c) 40

d) 72

Instructions

The pie chart given below shows the percentage distribution of annual expenditure on various items of a company. The annual expenditure of the company is Rs. 70 Crores.

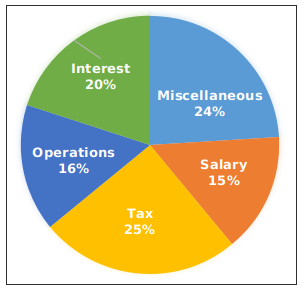
Question 25: Total amount spent on Raw material is 50% of the total amount spent on Interest. If the ratio of amount of expenditure on Rent and Raw material is 1 : 2 respectively, then what will be the amount (in Rs) spent on Rent annually?

a) 28000000

b) 35000000

c) 40000000

d) 32000000

Question 26: How much is the expenditure (in Rs crores) on Operations annually?

a) 10.2

b) 7.14

c) 11.2

d) 112

Question 27: Raman, Rohit and Raja are partners and invest in a business. Raman invests 1/4th of total and Rohit invest 1/3th of the total. What is the ratio of profit of Raman, Rohit and Raja respectively?

a) 4 : 3 : 1

b) 3 : 4 : 4

c) 3 : 4 : 5

d) 4 : 3 : 5

Instructions

The given pie chart shows the distribution (in degrees) of cars sold of different models by a company in 2015-16.

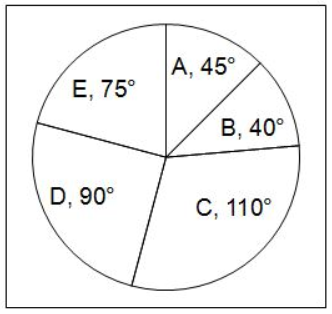
Question 28: If the number of cars sold of model D is 40500, what is the ratio between the number of cars sold of model D and E?

a) 9 : 5

b) 6 : 5

c) 11 : 9

d) 9 : 7

Question 29: In ΔABC, a line parallel to side BC cuts the side AB and AC at points D and E respectively and also point D divide AB in the ratio of 1 : 4. If area of ΔABC is 200 cm$^{2}$, then what is the area (in cm$^{2}$) of quadrilateral DECB?

a) 192

b) 50

c) 120

d) 96

Question 30: A circular wire of length 168 cm is cut and bent in the form of a rectangle whose sides are in the ratio of 5 : 7. What is the length (in cm) of the diagonal of the rectangle?

a) √4127

b) √3137

c) √1813

d) √3626

Question 31: What is the ratio of in-radius and circum-radius of an equilateral triangle?

a) 1 : 2

b) 1 : 3

c) 1 : 4

d) 3 : 2

Question 32: A cuboid which sides 6 cm, 9 cm and 32 cm is melted to form a new cube. What is the ratio between the total surface area of the cuboid and that of the cube?

a) 93 : 71

b) 108 : 113

c) 297 : 220

d) 89 : 72

Question 33: The ratio of curved surface area of two cones is 1 : 8 and the ratio of there slant heights is 1 : 4. What is the ratio of the radius of the two cones?

a) 1 : 1

b) 1 : 2

c) 1 : 4

d) 1 : 8

Question 34: The ratio of two numbers is 4 : 5. If both numbers are increased by 4, the ratio becomes 5 : 6. What is the sum of the two numbers?

a) 9

b) 18

c) 27

d) 36

Question 35: The ratio of syrup and water in a mixture is 3 : 1, then the percentage of syrup in this mixture is:

a) 25%

b) 66 $\ \frac{2}{3}$%

c) 33 $\ \frac{1}{3}$%

d) 75%

Question 36: Among the following statements, the statement which is not correct is:

a) Every natural number is a real number

b) Every real number is a rational number

c) Every integer is a rational number

d) Every natural number is an integer

Question 37: 20 liters of a mixture contains milk and water in the ratio 3 : 1. Then the amount of milk to be added to the mixture so as to have milk and water in the ratio 4 :1 is

a) 6 liters

b) 5 liters

c) 4 liters

d) 7 liters

Question 38: A vessel contains 60 litres of milk. 12 liters of milk taken out from it and replaced by water. Then again from mixture. 12 litres are again taken out and replaced by water. The ratio of milk and water in the resultant mixture is:

a) 16 : 10

b) 9 : 5

c) 15 : 10

d) 16 : 9

Question 39: The current ages of Sonali and Monali are in the ratio 5 : 3 Five years from now, their ages will be in the ratio 10 : 7 Then, Monali’s current age is

a) 9 years

b) 15 years

c) 3 years

d) 5 years

Question 40: If $a=\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$ and $b=\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$, then the value of $\frac{a^2}{b}+\frac{b^2}{a}$ is:

a) 98

b) 93

c) 103

d) 102

Stenographer Expected Cut off 2018-19

SSC Stenographer Salary after 7th Pay Commission

Answers & Solutions:

1) Answer (B)

2) Answer (B)

Let the present ages of x and y be 3a,4a respectively

After 5 years, their ages will be 3a+5 and 4a+5

$\frac{3a+5}{4a+5} = \frac{4}{5}$

==> 5(3a+5) = 4(4a+5)

==> 15a+25 = 16a+20

==> a=5

 

Present age of x = 3*5=15 years

Present age of y = 4*5=20 years

3) Answer (C)

Let the amount distributed among P, Q and R be 5x, 9x and 17x respectively

Total shares of P and Q is 7,000 (given) i.e

$\Rightarrow$ 5x + 9x = 7,000

$\Rightarrow$ 14x = 7,000 (or) x = 500

$\therefore$ R’s share = 17(500) = 8,500

Hence, option C is the correct answer.

4) Answer (D)

Gold is 19 times as heavy as water i.e G = $19W$

Copper is 9 times as heavy as water i.e C = $9W$

Let both the metals be mixed in the ratio of $A : B$. Then,

$\frac{A(G)}{A + B} + \frac{B(C)}{A + B} = 15W$

$A(19W)+ B(9W) = 15W(A + B)$

$19A+ 9B = 15A + 15B$

$4A = 6B$

$A : B = 3 : 2$

Hence, option D is the correct answer.

5) Answer (B)

Let the present ages of x and y be $3x$ and $x$

The ratio between the ages of x and y after 15 years will be 2:1

$\Rightarrow \frac{3x + 15}{x + 15} = \frac{2}{1}$

$\Rightarrow 3x + 15 = 2x + 30$

$\Rightarrow x = 15$

$\therefore$ Present ages of x and y are 45 and 15 respectively.

Hence, option B is the correct answer.

DAILY FREE SSC PRACTICE SET

 

6) Answer (B)

Let the number of Boys be ‘B’ and the number of girls be ‘G’

$\frac{1}{10}$B=$\frac{1}{4}G$

$\Rightarrow\frac{B}{G}$= $\frac{5}{2}$

$\therefore$ B:G=5:2

 

7) Answer (C)

Given that the perimeters of rectangle and triangle are equal

Let the length and breadth of rectangle be ‘l’ and ‘b’ respectively

Let the side of triangle be ‘a’

$\Rightarrow$ 2(l+b)=3a

Given that one side of rectangle of rectangle = side of triangle

Let l=a

$\Rightarrow$ 2(a+b)=3a
$\Rightarrow$ 2a+2b=3a
$\Rightarrow$ a=2b

Area of rectangle : Area of triangle = ab : $\frac{\sqrt{3}}{4}a^{2}$

Substituting a=2b in above equation

$\Rightarrow$ $2b^{2} : \frac{\sqrt{3}}{4}\times4b^{2}$

$\Rightarrow 2:\sqrt{3}$

8) Answer (D)

9) Answer (D)

$\frac{5+\sqrt{11}}{3-2\sqrt{11}} = x+y\sqrt{11}$

Rationalising above equation

$\frac{5+\sqrt{11}}{3-2\sqrt{11}}\times \frac{3+2\sqrt{11}}{3+2\sqrt{11}} = x+y\sqrt{11}$

$\Rightarrow \frac{15+10\sqrt{11}+3\sqrt{11}+22}{9-44} = x+y\sqrt{11}$

$\Rightarrow \frac{37+13\sqrt{11}}{-35} = x+y\sqrt{11}$

$\Rightarrow$ ($\frac{-37}{35})$+($\frac{-13}{35}$)$\sqrt{11} =$ $x+y\sqrt{11}$

Comparing above equations

x $= \frac{-37}{35}$ and y $= \frac{-13}{35}$

10) Answer (A)

Ratio between angles= 3:4:5

Total parts=3+4+5=12 parts

Total angle in triangle=$180^\circ$

12 parts$\rightarrow 180^\circ$

then 1 part$\rightarrow 15^\circ$

\therefore Angles in the triangle are

$15\times3=45^\circ$
$15\times4=60^\circ$
$15\times5=75^\circ$

 

FREE MOCK TEST FOR SSC STENOGRAPHER

11) Answer (C)

12) Answer (A)

13) Answer (C)

14) Answer (A)

15) Answer (A)

16) Answer (D)

17) Answer (B)

Expenditure (in %) in others = 15%

Expenditure on Marketing (in %) = $\frac{3}{(3+2)}\times15=9\%$

=> Central angle (in degrees) made by the sector of expenditure on Marketing = $\frac{9}{100}\times360^\circ$

= $32.4^\circ$

=> Ans – (B)

18) Answer (B)

19) Answer (B)

Let edge of cube = $a$ cm

Now, volume of cube = Volume of cuboid

=> $a^3=5\times10\times20$

=> $a=\sqrt[3]{1000}=10$ cm

Ratio between the total surface area of the cuboid and that of the cube = $\frac{2(lb+bh+hl)}{6a^2}$

= $\frac{2[(5\times10)+(10\times20)+(20\times5)]}{6\times(10)^2}$

=> $\frac{2\times(50+200+100)}{600}=\frac{700}{600}=\frac{7}{6}$

=> Ans – (B)

20) Answer (C)

Let radius of the cones be $r_1$ cm and $r_2$ cm respectively.

Slant height of first cone = $l_1=3$ cm and of second cone = $l_2=1$ cm

Curved surface area of cone = $\pi rl$

According to ques, => $\frac{\pi r_1l_1}{\pi r_2l_2}=\frac{1}{9}$

=> $\frac{r_1}{r_2}=\frac{1}{9}\times\frac{1}{3}=\frac{1}{27}$

Thus, the ratio of the radius of the two cones = 1 : 27

=> Ans – (C)

21) Answer (B)

Given : 3P = 5Q = 15R

Now, L.C.M. (3,5,15) = 15

=> P : Q : R = $(\frac{15}{3}):(\frac{15}{5}):(\frac{15}{15})$

= $5:3:1$

=> Ans – (B)

22) Answer (A)

Let the numbers be $5x$ and $11x$

According to ques,

=> $\frac{5x+10}{11x+10}=\frac{7}{13}$

=> $65x+130=77x+70$

=> $77x-65x=130-70$

=> $x=\frac{60}{12}=5$

$\therefore$ Sum of numbers = $5x+11x=16\times5=80$

=> Ans – (A)

23) Answer (D)

Total expenditure of company P, Q and S together (in %) = $(24+22+16)=62\%$

Total expenditure of all companies (in %) = $100\%$

=> Required ratio = $\frac{62}{100}=31:50$

=> Ans – (D)

24) Answer (B)

Let the numbers be $3x$ and $5x$

According to ques,

=> $\frac{3x+8}{5x+8}=\frac{13}{19}$

=> $57x+152=65x+104$

=> $65x-57x=152-104$

=> $x=\frac{48}{8}=6$

$\therefore$ Sum of numbers = $3x+5x=8\times6=48$

=> Ans – (B)

25) Answer (B)

Total amount spent on Interest = $\frac{20}{100}\times70=Rs.$ $14$ crores

=> Total amount spent on raw materials = $\frac{50}{100}\times14=Rs.$ $7$ crores

Ratio of amount of expenditure on Rent and Raw material = 1 : 2

=> Amount (in Rs) spent on Rent annually = $\frac{1}{2}\times7=Rs.$ $3.5$ crores

=> Ans – (B)

26) Answer (C)

Total expenditure = Rs. 70 crores

=> Expenditure (in Rs crores) on Operations annually = $\frac{16}{100}\times70=11.2$

=> Ans – (C)

27) Answer (C)

Raman invests 1/4th of total and Rohit invest 1/3th of the total

=> Raja’s investment = $1-\frac{1}{4}-\frac{1}{3}=\frac{12-3-4}{12}=\frac{5}{12}$

Thus, ratio of profit = $(\frac{1}{4}):(\frac{1}{3}):(\frac{5}{12})$

= $3:4:5$

=> Ans – (C)

28) Answer (B)

Ratio of cars sold by D and E is given by,

(90 degrees) : (75 degrees)

6 : 5

(Note: Here we can ignore the number of cars sold as we need to find the ratio)

Hence, option B is the correct answer.

29) Answer (A)

The ratio of AD and DB = 1: 4 (given)

Hence, the ratio of AD and AB can be taken as 1 : 5

$\triangle$ ADE, $\triangle$ ABC are similar triangles, so their areas will be in the ratio of 1 : 25 ($\because$ AD : AB = 1 : 5)

Total area of the triangle = 200

25x = 200 (or) x = 8 cm$^{2}$

Now, Area of ADE = 8 cm$^{2}$ and Area of DECB = 200 – 8 = 192 cm$^{2}$

Hence, option A is the correct answer.

30) Answer (D)

Let, length of the rectangle = 5x and breadth = 7x

A circular wire of length 168 cm is cut and bent in the form of rectangle i.e perimeter of the rectangle.

$\therefore$ 2(5x + 7x) = 168 $\Rightarrow$ 24x = 168 $\Rightarrow$ x = 7

Length = 35cm and Breadth = 49cm

Now, diagonal of the rectangle = $\sqrt{35^{2} + 49^{2}}$

$\Rightarrow\sqrt{1225 + 2401}\Rightarrow\sqrt{3626}$

Hence, option D is the correct answer.

31) Answer (A)

In case of an equilateral triangle In-radius(r) = $\frac{side}{2\sqrt{3}}$ and circum-radius(R) = $\frac{side}{\sqrt{3}}$

$\therefore$ Ratio between them = $\frac{side}{2\sqrt{3}}$ : $\frac{side}{\sqrt{3}}$

$\Rightarrow$ 1:2

Hence, option A is the correct answer.

32) Answer (D)

Given Length = 6 cm breadth = 9 cm height = 32 cm (of the cuboid)

Volume of both cube and cuboid will be same,

We know that volume of a cuboid = length x breadth x height and volume of the cube = a$^{3}$

$\therefore$ 6 x 9 x 32 = a$^{3}\Rightarrow$ a = 12

Now, surface area of the cuboid is given by,

2(lb + bh + hl) = 2(54 + 288 + 192) = 2 x 534 = 1068

surface area of the cube is given by,

6 a$^{2}$ = 6 (12)$^{2}$ = 864

Ratio of surface area of cuboid and surface area of cube = 1068 : 864 = 89 : 72

Hence, option D is the correct answer.

33) Answer (B)

Curved surface area of a cone = $\pi$rl (where l is the slant height of the cone)

Let, $l_{1} = x$ and $l_{2} = 4x$. Now the equation can be written as,

$\frac{\pi(r_{1})(x)}{\pi(r_{2})(4x)} = \frac{1}{8}$

$\frac{r_{1}}{r_{2}} = \frac{1}{2}$

Hence, option B is the correct answer.

34) Answer (D)

Let the two numbers be 4x and 5x.

If both numbers are increased by 4, the ratio becomes 5 : 6

4x + 4 : 5x + 4 = 5 : 6

6(4x + 4) = 5(5x + 4)

24x + 24 = 25x + 20

x = 4

Sum of 2 numbers (5x + 4x) = 9(4) = 36.

Hence, option D is the correct answer.

35) Answer (A)

Ratio of syrup and water in a mixture = 3 : 1

=> Percentage of syrup in this mixture = $\frac{1}{(3+1)}\times100$

= $\frac{100}{4}=25\%$

=> Ans – (A)

36) Answer (B)

The statement which is not correct is that every real number is a rational number.

Eg :- $\sqrt2$ is real but not rational.

=> Ans – (B)

37) Answer (B)

Ratio of milk and water in 20 litres mixture = 3:1

=> Quantity of milk = $\frac{3}{(3+1)}\times20=15$ litres

=> Quantity of water = $20-15=5$ litres

Let amount of milk added = $x$ litres

According to ques,

=> $\frac{15+x}{5}=\frac{4}{1}$

=> $15+x=20$

=> $x=20-15=5$

$\therefore$ The amount of milk to be added to the mixture so as to have milk and water in the ratio 4 :1 = 5 litres

=> Ans – (B)

38) Answer (D)

Initial quantity of milk = 60 litres

When 12 liters of milk taken out from it and replaced by water, then quantity of milk = $60-12=48$ litres and water = $12$ litres

(Total mixture still remains 60 litres)

Again, 12 litres of mixture is taken out, => Fraction of mixture taken out = $\frac{12}{60}=\frac{1}{5}^{th}$

=> Milk left = $48-(\frac{1}{5}\times48)=38.4$ litres

=> Water left = $60-38.4=21.6$ litres

$\therefore$ Required ratio = $\frac{38.4}{21.6}=\frac{64}{36}=16:9$

=> Ans – (D)

39) Answer (A)

Let current ages of Sonali and Monali are $5x$ and $3x$ years respectively.

According to ques,

=> $\frac{5x+5}{3x+5}=\frac{10}{7}$

=> $35x+35=30x+50$

=> $35x-30x=50-35$

=> $5x=15$

=> $x=\frac{15}{5}=3$

$\therefore$ Monali’s current age = $3\times3=9$ years

=> Ans – (A)

40) Answer (A)

Given : $a=\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$

Rationalizing the denominator, we get :

=> $a=\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\times\frac{(\sqrt3-\sqrt2)}{(\sqrt3-\sqrt2)}$

=> $a=\frac{(\sqrt3-\sqrt2)^2}{(\sqrt3+\sqrt2)(\sqrt3-\sqrt2)}$

=> $a=\frac{3+2-2(\sqrt3)(\sqrt2)}{(3-2)}$

=> $a=5-2\sqrt6$

Similarly, $b=5+2\sqrt6$

To find : $a^{2}+b^{2}$

= $(5-2\sqrt6)^2+(5+2\sqrt6)^2$

= $(25+24-20\sqrt6)+(25+24+20\sqrt6)$

= $49+49=98$

=> Ans – (A)

SSC STENOGRAPHER STUDY MATERIAL TOPIC-WISE

HIGHLY RATED PREPARATION APP

We hope this Ratio and Proportion questions for SSC Stenographer will be highly useful for your preparation.