Quantitative Aptitude Questions For SSC CHSL Exam
SSC CHSL Quantitative Aptitude Questions download PDF based on previous year question paper of SSC exams. 20 Very important Quantitative Aptitude questions for SSC CHSL Exam.
Download Quantitative Aptitude Questions For SSC CHSL Exam
Take a free mock test for SSC CHSL
Download SSC CHSL Previous Papers
Question 1: If $\sec \theta +\tan \theta=2$, then the value of $\sin \theta$ is:
a) $\frac{4}{5}$
b) $\frac{\sqrt{3}}{5}$
c) $\frac{2}{5}$
d) $\frac{3}{5}$
Question 2: If $\alpha + \theta$ = $\frac{7\pi}{12}$ and $\tan \theta = \sqrt{3}$, then the value of $\tan \alpha$ is:
a) $\sqrt{3}$
b) 1
c) 0
d) $\frac{1}{\sqrt{3}}$
Question 3: A person travelled from his home to his office at 48 km/hr and returned from his office to his home at 32 km/hr. Find his average speed.
a) 40 km/hr
b) 37.5 km/hr
c) 36 km/hr
d) 38.4 km/hr
Question 4: A train travelled from A to B at a speed of 60 km/hr and returned from B to A at a speed of 40 km/hr. Find the average speed of the train.
a) 50 km/hr
b) 48 km/hr
c) 42 km/hr
d) 56 km/hr
Question 5: A trader has 800 kg of sugar of which a part of it has been sold at 4% profit and the rest has been sold at 12% profit. On the whole, the profit is 8%. Find the quantity of sugar which he had sold it at 12% profit.
a) 360 kg
b) 500 kg
c) 280 kg
d) 400 kg
SSC CHSL Study Material (FREE Tests)
Question 6: A shopkeeper has 600 kg of rice of which a part of it has been sold at 6% profit and the rest has been sold at 4% loss. On the whole, he had no profit and no loss. Find the quantity which he had sold at loss.
a) 240 kg
b) 360 kg
c) 420 kg
d) 480 kg
Question 7: If ‘a’ is the root of the equation $x^{2}-5x+5=0$ and ‘b’ is the root of the equation $y^{2}-5y+5=0$, the what is the value of a+b ?
a) 10
b) 20
c) 0
d) 5
Question 8: Equation $x^{2}-bx+a=0$ has both of its roots as two consecutive numbers which are also prime numbers, then the value of $a^{2}-b^{2}$ ?
a) 11
b) 9
c) -11
d) -9
Question 9: Third term of an AP is 8 and the 7th term is 20. what is the ratio of sum of first 10 terms to the sum of first 20 terms ?
a) 155:620
b) 31:121
c) 31:122
d) 155:625
Question 10: If the sum of 31st term and 7th term of an arithmetic progression is 76 then find out the sum of first 37 terms of the A.P.?
a) 2812
b) 1330
c) 1406
d) 1735
Instructions
Question 11: Marked price of an article is Rs 1000 and three successive discounts of 20% each are given. What is the profit/loss if cost price=500 ?
a) Rs 14
b) Rs 12
c) Rs 13
d) Rs 11
Question 12: Marked price of an article is Rs 480 and cost price of article is marked up by 20%. If the profit percent is 20% then what is the discount offered ?
a) 10
b) 20
c) 30
d) 0
Instructions
Question 13: Which of the following number is divisible by both 3 and 9 ?
a) 349827
b) 739473
c) 650874
d) 835749
Question 14: If 83683h120 is divisible by 11 then what is the smallest value of h ?
a) 2
b) 5
c) 4
d) 6
Instructions
Question 15: Which of the following is least ?
$\frac{17}{13},\frac{18}{15},\frac{15}{9},\frac{12}{7}$
a) $\frac{17}{13}$
b) $\frac{18}{15}$
c) $\frac{15}{9}$
d) $\frac{12}{7}$
FREE SSC MATERIAL – 18000 FREE QUESTIONS
Question 16: Two linear equations 3x+5y=20, 24x+40y=K will have no solution for x and y when k = ?
a) 160
b) 8
c) 40
d) both b and c
Question 17: Find the number of factors of 13x if (7-$\frac{4x}{3}$)($\frac{3}{2}$)=$\frac{x}{6}$.
a) 12
b) 4
c) 8
d) 6
Instructions
Read the following pie chart and answer the questions given below.
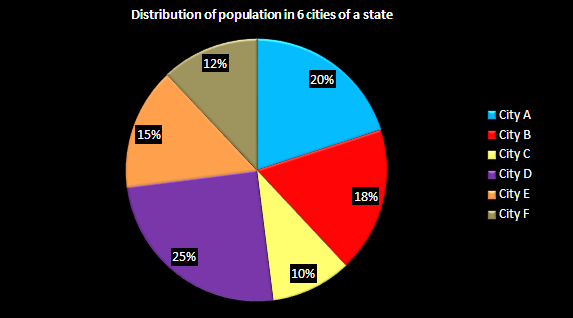
Question 18: Population of City A is how much percent more than that of City E?
a) 25%
b) 33.33%
c) 50%
d) 16.67%
Question 19: If the population of City C is 5 lakh less than that of City E, then what the population of City A?
a) 2 lakh
b) 20 lakh
c) 15 lakh
d) 10 lakh
Question 20: If the population of City B is 54 lakh, then what is the population of City E?
a) 40 lakh
b) 48 lakh
c) 45 lakh
d) 36 lakh
DOWNLOAD APP TO ACESSES DIRECTLY ON MOBILE
Answers & Solutions:
1) Answer (D)
Given : $\sec \theta +\tan \theta=2$ ———–(i)
Also, $sec^2\theta-tan^2\theta=1$
=> $(sec\theta-tan\theta)(sec\theta+tan\theta)=1$
=> $\sec \theta -\tan \theta=\frac{1}{2}$ ———-(ii)
Adding equations (i) and (ii), => $2sec\theta=2+\frac{1}{2}=\frac{5}{2}$
=> $sec\theta=\frac{5}{4}$
=> $cos\theta=\frac{4}{5}$
$\therefore$ $sin\theta=\sqrt{1-cos^2\theta}$
= $\sqrt{1-(\frac{4}{5})^2}=\sqrt{1-\frac{16}{25}}$
= $\sqrt{\frac{9}{25}}=\frac{3}{5}$
=> Ans – (D)
2) Answer (B)
Given : $\tan \theta = \sqrt{3}$
=> $\tan \theta = tan(\frac{\pi}{3})$
=> $\theta=\frac{\pi}{3}$
Also, $\alpha + \theta$ = $\frac{7\pi}{12}$
=> $\alpha=\frac{7\pi}{12}-\frac{\pi}{3}$
=> $\alpha=\frac{7\pi-4\pi}{12}=\frac{\pi}{4}$
$\therefore$ $tan\alpha=tan(\frac{\pi}{4})=1$
=> Ans – (B)
3) Answer (D)
Let the distance between his home and his office be 96 km. (LCM of 48 and 32)
Total distance = 96+96 = 192 km
Time required to travel 96 km at 48 km/hr = 2 hours
Time required to travel 96 km at 32 km/hr = 3 hours
Total time = 2+3 = 5 hours
Average speed $= \dfrac{\text{Total Distance}}{\text{Total Time}} = \dfrac{192}{5} = 38.4 km/hr$
4) Answer (B)
Let the distance between A and B be 120 km each (LCM of 60 and 40).
Time taken by the train to travel 120 km at 60 km/hr = 2 hours
Time taken by the train to travel 120 km at 40 km/hr = 3 hours
Total distance = 120+120 = 240 km
Total time = 2+3 = 5 hours
Average speed $= \dfrac{\text{Total Distance}}{\text{Total Time}} = \dfrac{240}{5} = 48 km/hr$
5) Answer (D)
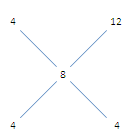
Quantity sold at 4% profit : Quantity sold at 12% profit = 4 : 4 = 1 : 1
Hence, the quantity of sugar he sold at 12% profit = $\dfrac{1}{2} \times 800 = 400 kg$
6) Answer (B)
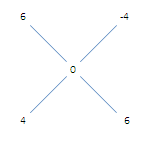
Quantity at 6% profit : Quantity at 4% loss = 4 : 6 = 2 : 3
Hence, The quantity of rice sold at loss = $\dfrac{3}{5} \times 600 = 360 kg$
7) Answer (D)
Substituting ‘a’ and ‘b’ in the equation we get $a^{2}-5a+5=0$
$b^{2}-5b+5=0$ so let us assume a equation $z^{2}-5z+5=0$
For this equation both a and b are the roots since they satisfy the equation.
Therefore sum of the roots =5.
8) Answer (A)
The only prime numbers that are consecutive are 2,3.
Substituting the values of $x=2 and x=3 $
We get $3^{2}-3b+a=0$ and
$2^{2}-2b+a=0$
Solving for a and b we get a=6 and b=5.
So $6^{2}-5^{2}=11$
9) Answer (C)
Given a+2d=8 and a+6d=20
We have d=3,a=2
sum of n terms of an AP=$\frac{n}{2}(2a+(n-1)d)$
For n=10,S=155
For n=20,S=610
Therefore required ratio =31:122
10) Answer (C)
Let us assume that first term and common difference of A.P. are ‘a’ and ‘d’ respectively.
$T_{7} + T_{31} = (a+6d) + (a+30d) = 76$
$2a + 36d = 76$ … (1)
Sum of first n terms of an A.P. = $\frac{n\times [2a+(n-1)d]}{2}$
Therefore sum of first 37 terms of the A.P. = $\frac{37\times [2a+(37-1)d]}{2}$
$\Rightarrow$ $\frac{37\times [2a+36d]}{2}$
$\Rightarrow$ $\frac{37\times 76}{2}$
$\Rightarrow$ $1406$ (Answer :C)
11) Answer (B)
MP=1000
Three successive discounts of 20% each and so SP=1000*(80/100)(80/100)(80/100)
SP=512
Profit=512-500
=12
12) Answer (D)
MP=480
1.2*CP=480
CP=400
SP=MP-d
SP=480-d
$\frac{480-d-400}{400}\times100$=20
80-d=80
d=0
13) Answer (D)
Sum of digits should be divisible by 9 is the required criteria and so
349827=3+4+9+8+2+7=33
739473=7+3+9+4+7+3=33
650874=6+5+0+8+7+4=30
835749=8+3+5+7+4+9=36
Hence d is the correct answer
14) Answer (B)
Divisibility test of 11 says that if the difference of sum of odd and even terms is divisible by 11 or 0 then it is divisible by 11
Sum of odd terms=8+6+3+1+0=18
Sum of even terms=3+8+h+2=13+h
difference=18-13-h
=5-h
Therefore for h=5 we have difference =0
15) Answer (B)
$\frac{17}{13}$=1.30
$\frac{18}{15}$=1.2
$\frac{15}{9}$=1.66
$\frac{12}{7}$=1.71
16) Answer (D)
For the given two equations 3x+5y=20 and 24x+40y=k
8(3x+5y)=k
3x+5y=($\frac{k}{8}$)
They have infinite solutions if k=160 and for all other values of k it will have no solution.
17) Answer (D)
solving the equation for x,
We get $\frac{21}{2}$=$2x+\frac{x}{6}$
$\frac{21}{2}$=$\frac{13x}{6}$
$x$=$\frac{63}{13}$
$13x$=63
Factorising 63 we get 63=$3^{2}\times 7$
Number of factors=(2+1)(1+1)
=6
18) Answer (B)
Let the total population of all the cities together be x
Population of City A = 20% of x = 0.2x
Population of City E = 15% of x = 0.15x
Required percentage = $\dfrac{0.20x-0.15x}{0.15x} \times 100 = \dfrac{0.5x}{0.15x} \times 100 = 33.33$%
19) Answer (B)
Let the total population of all the cities together be x
Population of City C = 10% of x
Population of City E = 15% of x
Given, 15% of x – 10% of x = 5 lakh
⇒ 5% of x =5 lakh
⇒ x = 100 lakh or 1 crore
Population of City A = 20% of 1 crore = 20 lakh
20) Answer (C)
Let the total population of all the cities together be x
Population of City B = 18% of x
Given, 18% of x = 54 lakh
⇒ $x = 5400000 \times \dfrac{100}{18} = 300$ lakh or 3 crore
Hence, Population of E = 15% of 300 lakh = 45 lakh





