Number Series Questions for SSC JE PDF
Download SSC JE Number Series Questions PDF. Top 15 SSC JE Number Series questions based on asked questions in previous exam papers very important for the SSC exam.
Download Number Series Questions for SSC JE PDF
Download SSC JE Previous Papers
Instructions
In the following five questions, select the missing number from the given responses.
Question 1: 
a) 1
b) 30
c) 11
d) 0
Instructions
In the following questions, select the missing number from the given responses.
Question 2:
a) 24
b) 27
c) 29
d) 22
Instructions
In each of the following questions, select the related word/letters/numbers from the given alternatives.
Question 3: $\frac{1}{8}:\frac{1}{64}::\frac{1}{16}:\frac{1}{?}$
a) 128
b) 126
c) 144
d) 132
Instructions
In each of the following questions, which one set of letters when sequentially placed at the gaps in the given letter series shall complete it ?
Question 4: Find out the wrong number in the sequence
102, 101, 98, 93, 86, 74, 66, 53
a) 101
b) 66
c) 74
d) 93
Question 5: 40% of 1620 + 30% of 960 = ? % of 5200
a) 12
b) 24
c) 16
d) 18
Question 6: What will come in place of the question mark (?) in the series?
3, 8, 27, 112, (?), 3396
a) 565
b) 452
c) 560
d) 678
Question 7: Find out the set of numbers amongst the four sets of numbers given in the alternatives which is most like the set given in the question.
Given Set : (8, 56, 72)
a) (7, 56, 63)
b) (3, 15, 24)
c) (6. 42, 54)
d) (5, 30, 35)
Instructions
In each of the following questions a series is given, with one/two term(s) missing. Choose the correct alternative from the given ones that will complete the series.
Question 8: 9, 8, 10, 16, 11, ?, 12, 64
a) 28
b) 36
c) 25
d) 32
Instructions
In each of the following questions, select the missing number from the given responses.
Question 9: 
a) 20
b) 25
c) 10
d) 15
Instructions
In each of the following questions, select the missing number from the given responses.
Question 10: 5 1 25
6 2 18
10 4 25
3 3 ?
a) 10
b) 9
c) 3
d) 4
Download RRB JE Previous Papers
Instructions
In each of the following questions, select the missing number from the given responses :
Question 11: 216 209 202
522 515 508
633 626 ?
a) 620
b) 608
c) 602
d) 619
Question 12: A series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
144, 256, 400, ?
a) 441
b) 576
c) 625
d) 289
Question 13: A series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
30, 60, 360, 3600, ?
a) 48500
b) 50500
c) 50400
d) 40800
Question 14: A series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
17, 27, 42, 62,?
a) 82
b) 87
c) 81
d) 84
Question 15: A series is given with one term missing. Select the correct alternative from the given ones that will complete the series.
2, 7, 16, ? , 46, 67
a) 26
b) 27
c) 29
d) 31
Answers & Solutions:
1) Answer (D)

let the missing term be y
here in 1st figure , the pattern is (3 x 2 x 4) = 24
in 2nd figure , (2 x -1 x -2 ) = 4
in 3rd figure also the same thing will be followed ,
y = (6 x 5 x 0 ) = 0
2) Answer (C)
The pattern followed is : Sum of first row and the positive difference between second and third rows.
=> 18 + (6-3) = 21 and 21 + (9-4) = 26
Similarly, 24 + (8-3) = 24 + 5 = 29
=> Ans – (C)
3) Answer (A)
$\frac{1}{8}:\frac{1}{64}$ = 8
let the missing number be y
$\frac{1}{16}:\frac{1}{y}$ = 8
y = 128
4) Answer (C)
here the given pattern is 102, 101, 98, 93, 86, 74, 66, 53
as we ca see that
102 – 101 = 1
101 – 98 = 3
98 – 93 = 5
93 – 86 = 7
as we can see that the difference between consecutive terms is increasing by 2 in every case but when we check
86 – 74 = 12 we see that the pattern is not getting fullfilled in case of 74 so in order to make the same pattern the term should be 77 inspite of 74 .
lets check with 77
86 – 77 = 9
hence it is confirmed that the wrong number is 74
5) Answer (D)
40% of 1620 = $\frac{40 \times 1620}{100}$ = $ 648 $
30% of 960 = $\frac{30 \times 960}{100}$ = $ 288 $
648 + 288 = 936
Let the unknown percentage be $x$.
$ 936 = x \% of 5200$
$x = \frac{936 \times 100}{5200} = 18 $
Hence option D is the correct answer.
6) Answer (A)
Let the missing term be y
here the sequence is 3, 8, 27, 112, y, 3396
here the pattern is :
8 = 3 x 2 + 2
27 = 8 x 3 + 3
112 = 27 x 4 + 4
so from the highlighted pattern , we can say that
y = 112 x 5 + 5 = 565
7) Answer (C)
(8, 56, 72)
follows the pattern
(8 , 8 x 7 , 8 x 9 )
So (6. 42, 54) is similar to (8, 56, 72)
as it follows the pattern
(6 , 6 x 7 , 6 x 9 )
8) Answer (D)
In the given question there are two series
Series 1
8, 8 x 2 = 16 , 16 x 2 =32 , 32 x 2 =64
Series 2
9,10,11,12
So option D is correct
9) Answer (D)
The product of 2 numbers in a sector is equal to the central number in the previous sector.
$3\times5=15$, $8\times3=24$
$2\times7=14$
Similarly, $5\times3=15$
=> Ans – (D)
10) Answer (C)
Each row of the given matrix follows the pattern
$ 5^{2}/1$ =25
$ 6^{2}/2$ =18
$ 10^{2}/4$ =25
$ 3^{2}/3$ =3
11) Answer (D)
In each row the next term is obtained by subtracting 7 from the previous term
In Row 1
216,216-7 =209,209-7 =202
In Row 2
522,522-7 =515 ,515-7 =508
In Row 3
633, 633-7 =626, 626-7 =619
So ? = 619
12) Answer (B)
The pattern followed is :

Thus, $24^2=576$
=> Ans – (B)
13) Answer (C)
Expression : 30, 60, 360, 3600, ?
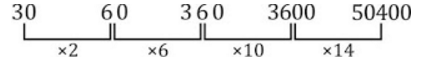
Thus, missing number = 50400
=> Ans – (C)
14) Answer (B)
Multiples of 5 are added.
17 + 10 = 27
27 + 15 = 42
42 + 20 = 62
62 + 25 = 87
=> Ans – (B)
15) Answer (C)
Numbers with difference of 4 are added.
2 + 5 = 7
7 + 9 = 9
16 + 13 = 29
29 + 17 = 46
46 + 21 = 67
=> Ans – (C)
Download SSC JE Previous Papers
We hope this Number Series Questions pdf for SSC JE exam will be highly useful for your Preparation.






