Mensuration Questions for SSC-CPO Set-2 PDF
Download SSC CPO Mensuration Questions with answers set-2 PDF based on previous papers very useful for SSC CPO exams. Very important Mensuration Questions for SSC exams.
Download Mensuration Questions for SSC CPO Set-2 PDF
Take a free mock test for SSC CPO
Download SSC CPO Previous Papers PDF
Question 1: The circumference of a circle is 88 cm. Find its radius (in cm).
a) 28
b) 15
c) 14
d) 30
Question 2: The volume of a hemisphere is 19404 cm3. Find its diameter (in cm).
a) 42
b) 21
c) 84
d) 63
Question 3: If the perimeter of a semicircle is 36 cm, then find its area (in $cm^{2}$)
a) 154
b) 35
c) 77
d) 70
Question 4: The lengths of the two diagonals of a rhombus are 7 cm and 24 cm. Find the length of its perimeter (in cm).
a) 25
b) 100
c) 75
d) 50
Question 5: Find the total surface area (in $cm^{2}$) of a right circular cone of diameter 21 cm and slant height 11 cm.
a) 467.5
b) 384
c) 724
d) 709.5
Download SSC CPO Previous Papers PDF
Question 6: Calculate the area (in $cm^{2}$) of a circle of radius 17.5 cm.
a) 1925
b) 962.5
c) 809.5
d) 1619
Question 7: The area of an equilateral triangle is 25√3 $cm^{2}$. Find its side (in cm).
a) 10
b) 5
c) 20
d) 30
Question 8: Find the total surface area $(in cm^2)$ of a cuboid of length, breadth and height of 10.5 cm, 8 cm and 9 cm respectively.
a) 607
b) 767
c) 769
d) 501
Question 9: The length of the diagonal and the breadth of a rectangle is 26 cm and 10 cm respectively. Calculate its area $(in cm^2)$
a) 480
b) 96
c) 240
d) 192
Question 10: Find the total surface area (in cm²) of a right circular cylinder of diameter 42 cm and height 14 cm.
a) 4488
b) 4250
c) 4010
d) 4620
Answers & Solutions:
1) Answer (C)
Let radius of circle = $r$ cm
=> Circumference = $2\pi r=88$
=> $2\times\frac{22}{7}\times r=88$
=> $r=88\times\frac{7}{44}$
=> $r=2\times7=14$ cm
=> Ans – (C)
2) Answer (A)
Let radius of hemisphere = $r$ cm
Volume of hemisphere = $\frac{2}{3}\times\pi r^3$
=> $\frac{2}{3}\times\frac{22}{7}\times(r)^3=19404$
=> $(r)^3=19404\times\frac{21}{44}$
=> $(r)^3=441\times21$
=> $r=\sqrt[3]{21\times21\times21}=21$ cm
$\therefore$ Diameter = $2\times21=42$ cm
=> Ans – (A)
3) Answer (C)
Let radius of semi circle = $r$ cm
=> Perimeter of semi circle = $\pi r+2r=36$
=> $r(\frac{22}{7}+2)=36$
=> $r(\frac{22+14}{7})=36$
=> $r=36\times\frac{7}{36}=7$ cm
$\therefore$ Area of semi-circle = $\frac{1}{2} \pi r^2$
= $\frac{1}{2}\times\frac{22}{7}\times(7)^2$
= $11\times7=77$ $cm^2$
=> Ans – (C)
4) Answer (D)
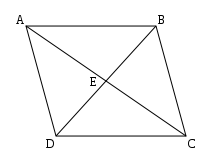
Given : ABCD is a rhombus and AC = 24 cm and BD = 7 cm
To find : Perimeter of ABCD
Solution : Diagonals of a rhombus bisect each other at right angle.
=> BE = $\frac{7}{2}=3.5$ cm and AE = $\frac{24}{2}=12$ cm
Thus, in right $\triangle$ AEB,
=> $(AB)^2=(AE)^2+(BE)^2$
=> $(AB)^2=(12)^2+(3.5)^2$
=> $(AB)^2=144+12.25=156.25$
=> $AB=\sqrt{156.25}=12.5$ cm
$\therefore$ Perimeter of rhombus ABCD = $4\times12.5=50$ cm
=> Ans – (D)
5) Answer (D)
Radius of cone, $r=\frac{21}{2}=10.5$ cm and slant height, $l=11$ cm
Total surface area of cone = $\pi r(l+r)$
= $\frac{22}{7}\times10.5\times(10.5+11)$
= $33\times21.5=709.5$ $cm^2$
=> Ans – (D)
6) Answer (B)
Radius of circle = $r=17.5$ cm
=> Area = $\pi r^2$
= $\frac{22}{7}\times17.5\times17.5$
= $22\times2.5\times17.5=962.5$ $cm^2$
=> Ans – (B)
7) Answer (A)
Let side of equilateral triangle = $s$ cm
=> Area = $\frac{\sqrt3}{4} s^2=25\sqrt3$
=> $\frac{s^2}{4}=25$
=> $s^2=25\times4=100$
=> $s=\sqrt{100}=10$ cm
=> Ans – (A)
8) Answer (D)
Length, $l=10.5$ cm, breadth, $b=8$ cm and height, $h=9$ cm
Total surface area of cuboid = $2(lb+bh+hl)$
= $2[(10.5\times8)+(8\times9)+(9\times10.5)]$
= $2\times(84+72+94.5)$
= $2\times250.5=501$ $cm^2$
=> Ans – (D)
9) Answer (C)
Let the length of rectangle = $l$ cm and breadth, $b=10$ cm
=> Diagonal, $d^2=l^2+b^2$
=> $l^2=(26)^2-(10)^2$
=> $l^2=676-100=576$
=> $l=\sqrt{576}=24$ cm
$\therefore$ Area = $24\times10=240$ $cm^2$
=> Ans – (C)
10) Answer (D)
Height of cylinder, $h=14$ cm and radius, $r=\frac{42}{2}=21$ cm
Total surface area of cylinder = $2\pi r(r+h)$
= $2\times\frac{22}{7}\times21\times(21+14)$
= $132\times35=4620$ $cm^2$
=> Ans – (D)
DOWNLOAD APP FOR SSC FREE MOCKS
We hope this Mensuration Set-2 PDF Questions for SSC CPO Exam will be highly useful for your preparation.





