Mensuration Questions for SSC CHSL Set-2 PDF
Download SSC CHSL Mensuration Questions with answers Set-2 PDF based on previous papers very useful for SSC CHSL Exams. Top-10 Very Important Mensuration Questions for SSC Exam
Download Mensuration Questions for SSC CHSL Set-2 PDF
Get 200 SSC mocks for just Rs. 249. Enroll here
Take a free mock test for SSC CHSL
Download SSC CHSL Previous Papers
More SSC CHSL Important Questions and Answers PDF
Question 1: A rectangle with one side of length 4 cm is inscribed in a circle of diameter 5 cm . Find area of the rectangle
a) $21 cm^2$
b) $12 cm^2$
c) $4 cm^2$
d) $3 cm^2$
Question 2: If G is the centroid of triangle ABC and area of triangle ABC = 48cm2, then the area of triangle BGC is
a) 8 cm2
b) 16 cm2
c) 24 cm2
d) 32 cm2
Question 3: In APQR, the line drawn from the vertex P intersects QR at a point S. If QR = 4.5 cm and SR = 1.5 cm then the ratios of the area of triangle PQS and triangle PSR is
a) 4 : 1
b) 3 : 1
c) 3 : 2
d) 2 : 1
Question 4: If G is the centroid and AD, BE, CF are three medians of triangle ABC with area 72 sq cm , then the area of triangle BDG is :
a) 12 sq cm
b) 16 sq cm
c) 24 sq cm
d) 8 sq cm
Question 5: The three medians AD, BE and CF of triangle ABC intersect at point G. If the area of triangle ABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
a) 10 sq.cm
b) 15 sq.cm
c) 20 sq.cm
d) 30 sq.cm
Take a free mock tests for SSC CHSL
SSC CHSL Study Material (FREE Tests)
Question 6: Length and breadth of a rectangle are increased by 40% and 70% respectively. What will be the percentage increase in the area of rectangle?
a) 118
b) 110
c) 138
d) 128
Question 7: In the given figure, PM is one-third of PQ and PN is one-third of PS. If the area of PMRN is 17 cm2, then what is the area $(in cm^2)$ of PQRS?
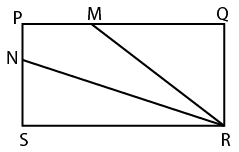
a) 34
b) 51
c) 68
d) 85
Question 8: In ΔABC, a line through A cuts the side BC at D such that BD : DC = 4 :5. If the area of ΔABD = 60 cm , then the area of ΔADC is
a) 90 cm²
b) 50 cm²
c) 60 cm²
d) 75 cm²
Question 9: If D, E and F are the mid points of BC, CA and AB respectively of the AABC then the ratio of area of the parallelogram DEFB and area of the trapezium CAFD is :
a) 2 : 3
b) 3 : 4
c) 1 : 2
d) 1 : 3
Question 10: ABC is a right angled triangle. B being the right angle. Midpoints of AB,BC and AC are respectively B’,C’ and A’. Area of ΔA’B’C’ is
a) $\frac{1}{2}$ x area of AABC
b) $\frac{2}{3}$ x area of AABC
c) $\frac{1}{4}$ x area of AABC
d) $\frac{1}{8}$ x area of AABC
Get 200 SSC mocks for just Rs. 249. Enroll here
Answers & Solutions:
1) Answer (B)

Given : AB = 4 cm and AC = 5 cm
To find : Area of rectangle ABCD = ?
Solution : In $\triangle$ ABC,
=> $(BC)^2=(AC)^2-(AB)^2$
=> $(BC)^2=(5)^2-(4)^2$
=> $(BC)^2=25-16=9$
=> $BC=\sqrt{9}=3$ cm
$\therefore$ Area of rectangle ABCD = $AB \times BC$
= $4 \times 3=12$ $cm^2$
=> Ans – (B)
2) Answer (B)
As we know area of triangle, with centroid as one of the vertices and remaining 2 triangle vertices, is $\frac{1}{3}$rd of the area of whole triangle.
Hence area will be $\frac{48}{3}$ = 16
3) Answer (D)
NOTE :- The ratio of area of two triangles on same base is equal to the ratio of two corresponding sides of the two triangles.
Given : QR = 4.5 cm and SR = 1.5 cm
=> QS = QR – SR = 4.5-1.5 = 3 cm
Since, the two triangles PQS and PSR have same base PS
=> $\frac{area(\triangle PQS)}{area(\triangle PSR)} = \frac{QS}{SR}$
= $\frac{3}{1.5}$ = 2 : 1
4) Answer (A)
The area of triangle formed by any two vertices and centroid is (1/3) times the area of ABC.
Also the median divides the triangle into two equal areas.
So, area of BDG = (1/6) times of ABC
= (1/6)*72
=12
5) Answer (C)
Given ∆ABC, G is the centroid and AD,BE, CF are three medians and the area of ∆AGE = 10
As we know the median divides the triangle into 6 triangles of equal area
Hence area of the quadrilateral BDGF = 2*∆AGE = 2*10
area of the quadrilateral BDGF = 20
SSC CHSL Study Material (FREE Tests)
6) Answer (C)
Let length and breadth of rectangle initially be $10$ units
=> Area, $A=10\times10=100$ sq.units
Length is increased by 40%, => New length = $10+(\frac{40}{100}\times10)=14$ units
Similarly, new breadth = $10+(\frac{70}{100}\times10)=17$ units
=> New area, $A’=14\times17=238$ sq.units
$\therefore$ % increase in area = $\frac{(238-100)}{100}\times100=138\%$
=> Ans – (C)
7) Answer (B)
Let PQ = SR = $3l$ and PS = QR = $3b$ cm
=> QM = $2l$ and NS = $2b$
Let the area of rectangle PQRS = $9lb=x$ $cm^2$ ————–(i)
=> Area of rectangle PQRS = Area of PMNR + ar($\triangle$ NSR) + ar($\triangle$ QMR)
=> $x=17+(\frac{1}{2}\times NS\times SR)+(\frac{1}{2}\times QM\times QR)$
=> $x=17+(\frac{1}{2}\times2b\times3l)+(\frac{1}{2}\times2l\times3b)$
=> $x=17+6lb$
Multiplying equation (i) by $\frac{2}{3}$, => $6lb=\frac{2x}{3}$
=> $x-\frac{2x}{3}=17$
=> $x=17\times3=51$ $cm^2$
=> Ans – (B)
8) Answer (D)
Let BD = 4$x$ and DC = 5$x$
Let height of the triangle be $h$ which will be same for both triangles ABD and ADC.
Now, area of $\triangle$ABD = $\frac{1}{2} * BD * h$ = 60
=> $\frac{1}{2} * 4x * h$ = 60
=> $xh$ = 30
Now, area of $\triangle$ADC = $\frac{1}{2} * DC * h$
= $\frac{1}{2} * 5x * h = \frac{1}{2} * 5 * 30$
= 75 $cm^2$
9) Answer (A)
Let , each side of the triangle be 2x.
So, AF=FB=BD=DC=CE=EA= x . EF=FD=DE=x ( as always EF= half of BC)
area of the parallelogram DEFB is $ base\times height$ = $ (x)\times h_p$
& area of the trapezium CAFD is $\frac{1}{2}\times base\times height$ = $\frac{1}{2}\times (x+2x)\times h_t$
Clearly , both the heights are to be measured from midpoint of sides to midpoints of the line joining the midpoints of the side. So , $h_p = h_t$ .
ratio of area of the parallelogram DEFB and area of the trapezium CAFD is
= $\frac{(x)\times h_p}{\frac{1}{2}\times (x+2x)\times h_t}$
= 2 : 3
10) Answer (C)
The triangle obtained by joining the midpoints will also be a right angled triangle.
Since the sides are reduced by a factor of 2, the area will be reduced by a factor of 4. (Since area = 0.5*b*h)
Option C is the right answer.
DOWNLOAD APP TO ACESSES DIRECTLY ON MOBILE
We hope this Mensuration Questions for SSC CHSL Exam preparation is so helpful to you.







