Mensuration Questions for SSC CHSL PDF:
SSC CHSL Mensuration Questions download PDF based on previous year question paper of SSC exams. 25 Very important Mensuration questions for SSC CHSL Exam.
Download Mensuration Questions for SSC CHSL PDF
SSC CHSL Study Material (FREE Tests)
Question 1: The ratio of the volume of a cube to that of a sphere which will fit inside the cube is
a) 4 : $\pi$
b) 4 : $3\pi$
c) 6: $\pi$
d) 2 : $\pi$
Question 2: If the ratio of volume of two cubes is 11 : 13, then what is the ratio of the sides of the two cubes ?
a) 11 : 13
b) 121 : 169
c) $(11)^{\frac{1}{2}}:(13)^{\frac{1}{2}}$
d) $(11)^{\frac{1}{3}}:(13)^{\frac{1}{3}}$
Question 3: If the square of sum of three positive consecutive natural numbers exceeds the sum of their squares by 292, then what is the largest of the three numbers?
a) 5
b) 6
c) 7
d) 8
Question 4: Two concentric circles are drawn with radii 12 cm and 13 cm. What will be the length of any chord of the larger circle that is tangent to the smaller circle ?
a) 5 cm
b) 8 cm
c) 10 cm
d) 25 cm
Question 5: In the figure below, AB is a chord of a circle with center O. A tangent AT is drawn at point A so that $\angle$BAT= $50^{0}$. Then $\angle$ADB=?
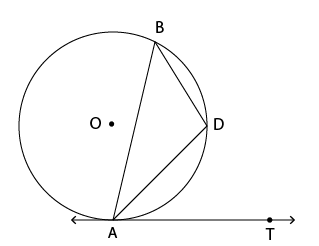
a) 120$^\circ$
b) 130$^\circ$
c) 140$^\circ$
d) 150$^\circ$
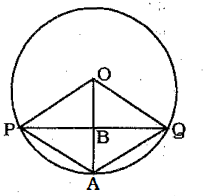
Question 6: Chord PQ is the perpendicular bisector of radius OA of circle with center O (A is a point on the edge of the circle). If the length of Arc PAQ = $\frac{2\pi}{3}$. What is the length of chord PQ ?
a) 2
b) $\sqrt{3}$
c) $2\sqrt{3}$
d) 1
Question 7: If $\frac{1}{x^{2}}+x^{2}$ represents the radius of circle P and $\ \frac{1}{x}+x=17$, which of the following best approximates the circumference of circle P ?
a) 287$\pi$
b) 547$\pi$
c) 574$\pi$
d) 278$\pi$
Question 8: The difference between circumference and the radius of a circle is 111 cm. What is the area (in $cm^{2}$) of the circle?
a) 469
b) 1386
c) 912
d) 1086
Question 9: A circle passing through points Q and R of triangle PQR, cuts the sides PQ and PR at points X and Y respectively. If PQ = PR, then what is the value (in degrees) of $\angle$PRQ + $\angle$QXY ?
a) 120
b) 150
c) 240
d) 180
Question 10: A,B and C are the three points on a circle such that $\angle$ABC = $35^{0}$ and $\angle$BAC = $85^{0}$. What is the angle (in degrees) subtended by arc AB at the center of the circle?
a) 60
b) 90
c) 135
d) 120
Question 11: If h,C,V are respectively the height, the curved surface and the volume of a cone, then $3\pi$ $Vh^{3}-C^{2}h^{2}+9V^{2}=$ ?
a) 0
b) 3
c) $\frac{1}{2}$
d) 11
Question 12: How many hemispherical balls can be made from a cylinder 56 cm high and 12 cm diameter, when every ball being 0.75 cm in radius ?
a) 1792
b) 3584
c) 4824
d) 7168
Question 13: On a rainy day, 60 cm of rain is recorded in a region. What is the volume of water collected in an open and empty rectangular water tank that measures 12 m (length) x 10 m (width) and 50 cm (depth) ?
a) 120 m$^{3}$
b) 72 m$^{3}$
c) 60 m$^{3}$
d) 48 m$^{3}$
Question 14: A prism with a right triangular base is 25 cm high. If the shorter sides of the triangle are in the ratio of 1 : 2 and the volume of the prism is $100 cm^{3}$, what is the length of the longest side of the triangle?
a) $\sqrt{5}\ $cm
b) $2\sqrt{5}\ $cm
c) $5\sqrt{2}\ $cm
d) 5 cm
Question 15: Two pipes can independently fill a bucket in 20 minutes and 25 minutes. Both are turned on together for 5 minutes after which the second pipe is turned off. What is the time taken by the first pipe alone to fill the remaining portion of the bucket ?
a) 11 minutes
b) 16 minutes
c) 20 minutes
d) 15 minutes
FREE SSC MATERIAL – 18000 FREE QUESTIONS
Question 16: If the diameter of a sphere is 14 cm., then what is the curved surface area (in $cm.^{2}$) of the sphere?
a) 616
b) 1232
c) 2464
d) 576
Question 17: Three numbers are such that their sum is 50, product is 3750 and the sum of their reciprocals is $\frac{31}{150}$. Find the sum of the squares of the three numbers.
a) 2500
b) 1250
c) 950
d) 122
Question 18: A vertical pole AB is standing at the centre B of a square PQRS. If PR subtends an angle of $90^{0}$at the top A of the pole, then the angle subtended by a side of the square at A is:
a) $30^{0}$
b) $45^{0}$
c) $60^{0}$
d) None of these
Question 19: ABCD is a square. Draw an equilateral triangle PBC on side BC considering BC is a base and an equilateral triangle QAC on digonal AC considering AC is a base. Find the value of $\ \frac{Area \ of \ \triangle PBC}{Area \ of \ \triangle QAC}$
a) $\frac{1}{2}$
b) 1
c) $\frac{1}{3}$
d) $\frac{1}{4}$
Question 20: A string of length 24 cm is bent first into a square and then into a right-angled triangle by keeping one side of the square fixed as its base. Then the area of triangle equals to:
a) 24 cm$^{2}$
b) 60 cm$^{2}$
c) 40 cm$^{2}$
d) 28 cm$^{2}$
DOWNLOAD APP TO ACESSES DIRECTLY ON MOBILE
Question 21: The diagonals of two squares are in the ratio of 3: 7. What is the ratio of their areas ?
a) 3 : 7
b) 9 : 49
c) 4 : 7
d) 7 : 3
Question 22: If the area of a square is increased by 44%, retaining its shape as a square, each of its sides increases by:
a) 19%
b) 21%
c) 22%
d) 20%
Question 23: Triangle ΔXYZ is similar to ΔPQR. If XY:PQ=5:1. If Area of ΔPQR is 5 sq cm, what is the area (in sq cm) of ΔXYZ?
a) 125
b) 120
c) 100
d) 64
Question 24: The diagonal of a square is 12 cm what is the length (in cm) of its side?
a) 6√2
b) 12√2
c) 6
d) 9
Question 25: Which of the following statements is not correct ?
a) For a given radius and height, a right circular cone has the lesser volume among a right circular cone and a right circular cylinder.
b) If side of a cube is increased by 10%, the volume will increase by 33.1%.
c) If the radius of a sphere is increased by 20%, the surface area will increase by 40%.
d) Cutting a sphere into 2 parts does not change the total volume.
FREE MOCK TEST FOR SSC STENOGRAPHER
Answers & Solutions:
1) Answer (C)
Let edge of cube be $2a$ cm and thus diameter of sphere = $2a$ cm
=> Radius of sphere = $\frac{2a}{2}=a$ cm
Volume of cube = $(2a)^3=8a^3$ $cm^3$ ———–(i)
Volume of sphere = $\frac{4}{3}\pi r^3$
= $\frac{4}{3} \pi \times(a)^3=\frac{4a^3\pi}{3}$ $cm^3$ ———–(ii)
Dividing equation (i) by (ii), we get :
=> Required ratio = $\frac{8a^3}{\frac{4a^3\pi}{3}}$
= $\frac{8\times3}{4\pi}=\frac{6}{\pi}$
$\therefore$ Ratio of the volume of a cube to that of a sphere which will fit inside the cube = $6:\pi$
=> Ans – (C)
2) Answer (D)
Let side of the two cubes be $a$ and $b$ units respectively
Ratio of volumes = $\frac{a^3}{b^3}=\frac{11}{13}$
=> $\frac{a}{b}=(\sqrt[3]{\frac{11}{13}})$
=> $\frac{a}{b}=(11)^{\frac{1}{3}}:(13)^{\frac{1}{3}}$
=> Ans – (D)
3) Answer (D)
Le the three positive consecutive natural numbers be $(x-1),(x),(x+1)$
According to ques,
=> $[(x-1)+(x)+(x+1)]^2-[(x-1)^2+(x)^2+(x+1)^2]=292$
=> $(3x)^2-[(x^2-2x+1)+(x^2)+(x^2+2x+1)]=292$
=> $9x^2-3x^2-2=292$
=> $6x^2=292+2=294$
=> $x^2=\frac{294}{6}=49$
=> $x=\sqrt{49}=7$
$\therefore$ Largest of the three numbers = $7+1=8$
=> Ans – (D)
4) Answer (C)
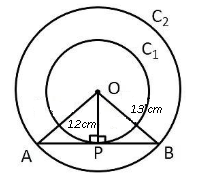
Given : $C_1$ and $C_2$ be the two concentric circles having radius $r_1=13$ cm and $r_2=12$ cm respectively.
To find : AB = ?
Solution : AB is the the tangent to the circle $C_1$, hence $\angle$ OPB = $90^\circ$
Also, the perpendicular from the centre of a circle to a chord bisects the chord.
Thus, in $\triangle$ OPB,
=> $(PB)^2=(OB)^2-(OP)^2$
=> $(PB)^2=(13)^2-(12)^2$
=> $(PB)^2=169-144=25$
=> $PB=\sqrt{25}=5$ cm
$\therefore$ AB = $2\times5=10$ cm
=> Ans – (C)
5) Answer (B)
6) Answer (B)
.
PQ is perpendicular bisector of OA. Also, OP = OQ (radii)
Hence, OPAQ is a rhombus. ————–(i)
Also, $2\angle PAQ=$ reflex $\angle POQ$ [The angle subtended at the centre by an arc is twice to that at the circumference]
=> $2\angle PAQ=360^\circ-\angle POQ$
=> $2\angle PAQ+\angle POQ=360^\circ$
From (i), we have $\angle PAQ=\angle POQ$
=> $3\angle POQ=360^\circ$
=> $\angle POQ=120^\circ=\frac{2\pi}{3}$
We know that, $r=\frac{l}{\theta}$
=> $r=\frac{\frac{2\pi}{3}}{\frac{2\pi}{3}}=1$ unit
In $\triangle$ POB,
=> $sin(\angle POB)=\frac{PB}{OP}$
=> $sin(60^\circ)=\frac{PB}{1}$
=> $PB=\frac{\sqrt3}{2}$
$\therefore$ Chord PQ = $2\times(PB)=2\times\frac{\sqrt3}{2}=\sqrt3$
=> Ans – (B)
7) Answer (C)
Given : $\ \frac{1}{x}+x=17$
Squaring both sides,
=> $(\frac{1}{x}+x)^2=(17)^2$
=> $x^2+\frac{1}{x^2}+2=289$
=> $x^2+\frac{1}{x^2}=289-2=287$
=> Radius of circle = $r=287$
$\therefore$ Circumference = $2\pi r$
= $2\times\pi\times287=574\pi$
=> Ans – (C)
8) Answer (B)
Let radius of circle = $r$ cm
=> $2\pi r-r=111$
=> $r(2\times\frac{22}{7}-1)=111$
=> $r\times\frac{44-7}{7}=111$
=> $r=111\times\frac{7}{37}=21$ cm
$\therefore$ Area of circle = $\pi r^2$
= $\frac{22}{7}\times(21)^2=1386$ $cm^2$
=> Ans – (B)
9) Answer (D)
10) Answer (D)
11) Answer (A)
Let slant height of cone = $l$ units and radius = $r$ units
Thus, $l=\sqrt{h^2+r^2}$ , $V=\frac{1}{3}\pi r^2h$ and $C=\pi rl$
To find : $3\pi$ $Vh^{3}-C^{2}h^{2}+9V^{2}$
= $[3\pi\times(\frac{1}{3}\pi r^2h)\times h^3]-[(\pi rl)^2\times h^2]+[9\times(\frac{1}{3}\pi r^2h)^2]$
= $[\pi^2 r^2h^4]-[\pi^2r^2h^2(r^2+h^2)]+[\pi^2r^4h^2]$
= $(\pi^2 r^2h^4)-(\pi^2r^4h^2)-(\pi^2r^2h^4)+(\pi^2r^4h^2)$
= $0$
=> Ans – (A)
12) Answer (D)
Radius of cylinder = $r=6$ cm and height = $h=56$ cm
=> Volume of cylinder = $\pi r^2h$
= $\pi\times(6)^2\times56=2016\pi$ $cm^3$
Radius of hemisphere = $R=0.75$ cm
=> Volume of hemisphere = $\frac{2}{3}\pi (R)^3$
= $\frac{2}{3}\pi\times(0.75)^3=0.28125\pi$ $cm^3$
$\therefore$ Number of balls made = $\frac{2016\pi}{0.28125\pi}=7168$
=> Ans – (D)
13) Answer (C)
14) Answer (B)
15) Answer (A)
Let capacity of bucket = L.C.M. (20,25) = 100 litres
First pipe can fill it in 20 minutes, => first pipe’s efficiency = $\frac{100}{20}=5$ l/min
Similarly, second pipe’s efficiency = $\frac{100}{25}=4$ l/min
=> Volume of bucket filled by both in five minutes = $(5+4)\times5=45$ litres
$\therefore$ Time taken by the first pipe alone to fill the remaining portion of the bucket = $\frac{(100-45)}{5}=11$ minutes
=> Ans – (A)
16) Answer (A)
Radius of sphere = 7 cm
Curved surface area = $4\pi r^2$
= $4\times\frac{22}{7}\times(7)^2=616$ $cm^2$
=> Ans – (A)
17) Answer (C)
Let the numbers be $x,y,z$
Given : $(x+y+z)=50$ , $xyz=3750$ and $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{31}{150}$
Now, $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{xy+yz+zx}{xyz}$
=> $(xy+yz+zx)=\frac{31}{150}\times3750=775$
$\therefore$ $(x+y+z)^2=x^2+y^2+z^2+2(xy+yz+zx)$
=> $(50)^2=(x^2+y^2+z^2)+2(775)$
=> $x^2+y^2+z^2=2500-1550=950$
=> Ans – (C)
18) Answer (C)
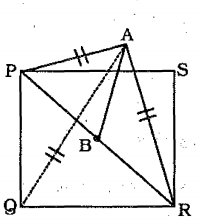
The pole is standing at the centre of the square, => PA = PR
=> $\angle$ APB = $\angle$ ARB = $45^\circ$
Let the side of the square = $x$ units
=> PR (diagonal) = $\sqrt2x$ units
Hence, PB = $\frac{x}{\sqrt2}$ units
Now, in $\triangle$ APB,
=> $tan(\angle APB)=\frac{AB}{PB}$
=> $tan(45^\circ)=1=\frac{AB}{PB}$
=> $AB=PB=\frac{x}{\sqrt2}$
Thus, $PA=\sqrt{(\frac{x}{\sqrt2})^2+(\frac{x}{\sqrt2})^2}$
=> $PA=\sqrt{\frac{x^2}{2}+\frac{x^2}{2}}=\sqrt{x^2}=x$
Similarly, $QA=x$ units
Hence, PA = PQ = QA = $x$
$\therefore$ $\angle$ PAQ = $60^\circ$
=> Ans – (C)
19) Answer (A)
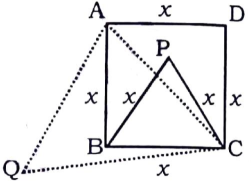
Let side of the square be $x$ cm
=> Side of equilateral $\triangle$ PBC = $x$ cm
In right $\triangle$ ABC,
=> $(AC)^2=(AB)^2+(BC)^2$
=> $(AC)^2=(x)^2+(x)^2=2x^2$
=> $AC=\sqrt2x$
$\therefore$ $\ \frac{ar(\triangle PBC)}{ar(\triangle QAC)}$
= $[\frac{\sqrt3}{4}\times (x)^2]\div[\frac{\sqrt3}{4}\times (\sqrt2x)^2]$
= $\frac{x^2}{2x^2}=\frac{1}{2}$
=> Ans – (A)
20) Answer (A)
String of length 24 cm is bent into square, => Perimeter of square = 24 cm
Let side of square = $a$ cm
=> $4a=24$
=> $a=\frac{24}{4}=6$ cm
Let the other side of triangle be $b$ and hypotenuse be $c$ cm
=> Perimeter of triangle = $a+b+c=24$
=> $b+c=24-6=18$
=> $c=18-b$ ————(i)
Also, using Pythagoras Theorem
=> $6^2+b^2=c^2$
=> $c^2-b^2=36$ ———–(ii)
Solving equations (i) and (ii), we get : $b=8$ cm and $c=10$ cm
$\therefore$ Area of triangle = $\frac{1}{2} ab$
= $\frac{1}{2}\times6\times8=24$ $cm^2$
=> Ans – (A)
21) Answer (B)
Ratio of square of diagonal to area of square = $2:1$
Let diagonal of first square = $d_1=3$ cm and $d_2=7$ cm
Thus, ratio of areas = $\frac{A_1}{A_2}=(\frac{d_1}{d_2})^2$
= $\frac{3^2}{7^2}=\frac{9}{49}$
=> Ans – (B)
22) Answer (D)
Let the side of square be $a=10$ cm
=> Area = $A=10\times10=100$ $cm^2$
New area = $100+(\frac{44}{100}\times100)=144$ $cm^2$
=> New side = $a’=\sqrt{144}=12$ cm
$\therefore$ Increase in area = $\frac{(12-10)}{10}\times100$
= $2\times10=20\%$
=> Ans – (D)
23) Answer (A)
Given : $\triangle XYZ \sim \triangle PQR$ and XY:PQ=5:1
To find : ar($\triangle$ XYZ) = $x$ = ?
Solution : Ratio of areas of two similar triangles is equal to the ratio of square of the corresponding sides.
=> $\frac{ar(\triangle XYZ)}{ar(\triangle PQR)}=(\frac{XY}{PQ})^2$
=> $\frac{x}{5}=(\frac{5}{1})^2$
=> $\frac{x}{5}=\frac{25}{1}$
=> $x=25\times5=125$ $cm^2$
=> Ans – (A)
24) Answer (A)
Let side of square = $a$ cm
Diagonal of square = $d=12$ cm
=> $(a)^2+(a)^2=(d)^2$
=> $2a^2=(12)^2=144$
=> $a^2=\frac{144}{2}=72$
=> $a=\sqrt{72}=6\sqrt2$ cm
=> Ans – (A)
25) Answer (C)
(A) : Volume of cylinder = $\pi r^2h$
Volume of cone = $\frac{1}{3}\pi r^2h$
=> Volume of cone is lesser (one-third) than the volume of cylinder. Above statement is correct.
(B) : Let side of cube = $a=10$ cm
=> Volume of cube = $(10)^3=1000$ $cm^3$
New side after 10% increase = $10+(\frac{10}{100}\times10)=11$ cm
Thus, new volume = $(11)^3=1331$ $cm^3$
$\therefore$ Increase in volume = $\frac{(1331-1000)}{1000}\times100=33.1\%$
Thus, above statement is correct.
(C) : Let radius of sphere = $r=10$ cm
Surface area of sphere = $4\pi r^2=4\pi(10)^2=400\pi$ $cm^2$
After increasing the radius by 20%, new radius = $r’=10+(\frac{20}{100}\times10)=12$ cm
=> New surface area = $4\pi(12)^2=576\pi$ $cm^2$
$\therefore$ Increase in surface area = $\frac{(576-400)}{400}\times100=44\%$
Thus, above statement is not correct.
(D) : Cutting a sphere into 2 parts does not change the total volume because the sum of volume of the two hemispheres will be equal to the volume of sphere. Hence, it is also correct.
=> Ans – (C)





![How To Manage Time In CAT Exam? [Section-wise Tips] How to manage time in CAT exam ?](https://cracku.in/blog/wp-content/uploads/2018/09/fig-03-09-2018_10-54-46-218x150.jpg)