Mensuration Questions for SSC CGL PDF:
Download SSC CGL Mensuration questions with answers PDF based on previous papers very useful for SSC CGL exams. 25 Very important Mensuration objective questions for SSC exams.
Download Mensuration Questions for SSC CGL PDF
Question 1: A copper wire is bent in the form of an equilateral triangle, and has an area $121\sqrt{3}$ cm2 . If the same wire is bent into the form of a circle, the area(in cm2) enclosed by the wire in(Take $\pi = \frac{22}{7}$)
a) 364.5
b) 693.5
c) 346.5
d) 639.5
Question 2: An equilateral triangle of side 6cm has its corners cut off to form a regular hexagon. Area (in cm2) of this regular hexagon will be ?
a) $3\sqrt{3}$
b) $3\sqrt{6}$
c) $6\sqrt{3}$
d) $\frac{5\sqrt{3}}{2}$
Question 3: The area of an equilateral triangle is $25\sqrt{3}cm^2$. What is the perimeter of the triangle?
a) 10 cm
b) 20 cm
c) 30 cm
d) 40 cm
Question 4: If the length and breadth of a rectangle increases by 20% and 15% each, find the percentage increase in its area.
a) 35%
b) 42%
c) 36%
d) 38%
Question 5: A circle is circumscribed around an equilateral triangle of side 3 cm. What is the area of the circle (in $cm^2$)?
a) $\sqrt3 \pi$
b) $3 \pi$
c) $3\sqrt3 \pi$
d) $9\pi$
SSC CGL Previous Papers Download PDF
Question 6: The length of canvas, 75 cm wide required to build a conical tent of height 14m and the floor area 346.5 m2 is
a) 665 m
b) 860 m
c) 490 m
d) 770 m
Question 7: If two medians BE and CF of a triangle ABC, intersect each other at G and if BG = CG, ∠BGC = 60° and BC = 8 cm then area of the triangle ABC is
a) $96\sqrt{3} cm^{2}$
b) $64\sqrt{3} cm^{2}$
c) $48\sqrt{3} cm^{2}$
d) $48 cm^{2}$
Question 8: 5 persons will live in a tent. If each person requires 16m2 of floor area and 100m3 space for air then the height of the cone of smallest size to accommodate these persons would be
a) 16 metre
b) 10.25 metre
c) 20 metre
d) 18.75 metre
Question 9: If the altitude of an equilateral triangle is 12√3 cm, then its area would be :
a) $12 cm^{2}$
b) $144\sqrt{3} cm^{2}$
c) $72 cm^{2}$
d) $36 \sqrt{3} cm^{2}$
Question 10: The perimeters of a circle, a square and an equilateral triangle are same and their areas are C, S and T respectively. Which of the following statement is true ?
a) C = S =T
b) C > S > T
c) C < S < T
d) S < C < T
18000+ Questions – Free SSC Study Material
Question 11: A wire of length 44 cm is first bent to form a circle and then rebent to form a square. The difference of the two enclosed areas is
a) 44 cm2
b) 33 cm2
c) 55 cm2
d) 66 cm2
Question 12: The area of the iron sheet required to prepare a cone 24 cm high with base radius 7 cm is (Take $\pi = \frac{22}{7}$)
a) 408 cm2
b) 708 cm2
c) 804 cm2
d) 704 cm2
Question 13: On decreasing each side of an equilateral triangle by 2 cm, there is a decrease of 4√3 cm 2 in its area. The length of each side of the triangle is
a) 8 cm
b) 3 cm
c) 5 cm
d) 6 cm
Question 14: The height of an equilateral triangle is 15 cm. The area of the triangle is
a) 50√3 sq. cm.
b) 70√3 sq. cm.
c) 75√3 sq. cm.
d) 150√3 sq. cm.
Question 15: The radius of a circle is a side of a square. The ratio of the areas of the circle and the square is
a) 1 : π
b) π : 1
c) π: 2
d) 2 : π
Question 16: The height of an equilateral triangle is 15 cm. The area of the triangle is
a) 50√3 sq. cm.
b) 70√3 sq. cm.
c) 75√3 sq. cm.
d) 150√3 sq. cm.
Question 17: The diagonal of a square is equal to the side of an equilateral triangle. If the area of the square is 15√3 sq cm, what is the area of the equilateral triangle?
a) 45/√2 sq cm
b) 45√2 sq cm
c) 45 sq cm
d) 45/2 sq cm
Question 18: The area of an equilateral triangle is 9√3 sq cm, find height of the triangle?
a) 6 cm
b) $6\sqrt{3}$ cm
c) $3\sqrt{3}$ cm
d) 9 cm
Question 19: The diagonal of a square equals the side of an equilateral triangle. If the area of the square is 12 sq cm, what is the area of the equilateral triangle?
a) 12√3 sq cm
b) 6√3 sq cm
c) 12√2 sq cm
d) 24 sq cm
Question 20: From an equilateral triangle of side 4 cm, a triangle formed by joining the mid points of the original triangle is cut out. Find the remaining area (in sq. cm)
a) $3 \sqrt{3}$ sq. cm
b) $3$ sq. cm
c) $4\sqrt{3}$ sq. cm
d) $2 \sqrt{3}$ sq. cm
100+ Free GK Tests for SSC Exams
Question 21: The area of the equilateral triangle is $\frac{81\sqrt{3}}{4}$ cm$^2$. Find the height of this triangle.
a) $6\sqrt{3}$ cm
b) $4.5\sqrt{3}$ cm
c) $4\sqrt{3}$ cm
d) $8\sqrt{3}$ cm
Question 22: The perimeters of a square and an equilateral triangle are equal. If the diagonal of the square is 9 cm, what is the area of the equilateral triangle?
a) 18√3 sq cm
b) 9√3 sq cm
c) 18√2 sq cm
d) 9√2 sq cm
Question 23: The diagonal of a square equals the side of an equilateral triangle. If the area of the square is 6√3 sq cm, what is the area of the equilateral triangle?
a) 9√3 sq cm
b) 9 sq cm
c) 9√2 sq cm
d) 12 sq cm
Question 24: If the length of the side of an equilateral triangle is 6 cm, what is its area?
a) 18√3 sq cm
b) 36√3 sq cm
c) 27√3 sq cm
d) 9√3 sq cm
Question 25: The base of the prism is in shape of an equilateral triangle of side 11 cm. The height of the prism is 4$\sqrt{3}$ cm. What is the volume of the prism?
a) 447 cu. cm.
b) 363 cu. cm.
c) 219 cu. cm.
d) 394 cu. cm.
1500+ Free SSC Questions & Answers
Answers & Solutions:
1) Answer (C)
Area of equilateral triangle is $\frac{\sqrt{3}}{4} a^{2}$ where a is side of triangle
which is equals to $121{\sqrt{3}}$
or a = 22 and whole length of wire will be 66
from here when it is bend to make a circle, circumference will be $2\pi r$ = 66
r = 10.5
hence area of circle will be $\pi r^{2}$ = 346.5
2) Answer (C)
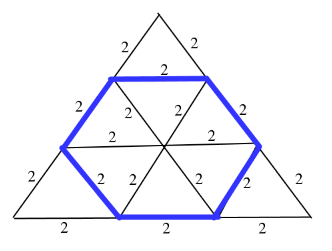
The hexagon is composed of 6 equilateral triangles, each with a side of 2.
Area of an equilateral triangle = $\frac{\sqrt3}{4}s^2$
=> Area of regular hexagon = 6 $\times$ area of small equilateral triangles
= $6\times\frac{\sqrt3}{4}\times(2)^2$
= $6\sqrt3$ $cm^2$
=> Ans – (C)
3) Answer (C)
Let the side of the triangle be ‘a’ cm
Area of the triangle = $\frac{\sqrt{3}a^2}{4}$
It is given that,
$\frac{\sqrt{3}a^2}{4}=25\sqrt{3}$
On solving we get $a=10$ cm
Thus the perimeter of the triangle will be $3*10=30$ cm
4) Answer (D)
Let L and B be the initial values of length and breadth respectively.
Therefore, the final values of length and breadth are 1.2L and 1.15B respectively.
Initial area of the rectangle = LB
Final area of the rectangle = 1.2*1.15 LB = 1.38 LB
Therefore, required percentage = ((1.38-1)LB/LB)*100 = 38%.
So, the correct option to choose is D.
5) Answer (B)
The circle is the circumcircle of the equilateral triangle.
Circumradius = $\frac{2}{3}*\frac{\sqrt3}{2}*3=\sqrt3$ cm
Area of the circle = $\pi*(\sqrt3)^2=3 \pi$ $cm^2$
Hence Option B.
6) Answer (D)
Base area = 346.5 $m^2$ = $\pi r^2$
=> $r^2 = \frac{346.5 * 7}{22}$
=> $r = \sqrt{110.25} = 10.5 m$
Height of tent = 14 m
Now, slant height$(l)$ of cone = $\sqrt{r^2 + h^2}$
=> $l = \sqrt{10.5^2 + 14^2}$
=> $l = \sqrt{306.25} = 17.5m$
Let length of cloth be $x$
Surface area of cone = $\pi rl$
=> $0.75 * x = \frac{22}{7} * 10.5 * 17.5$
=> $x = \frac{22 * 10.5 * 17.5}{7 * 0.75}$
=> $x = 770m$
7) Answer (C)
In Δ BGC
∠BGC = 60° and BG = GC
$\therefore$ ΔBGC is an isosceles triangle
∠GBC = ∠GCB
As, we know sum of angles of a triangle = 180°
$\therefore$ ∠GBC + ∠GCB + ∠BGC = 180°
=> 2∠GBC = 180° – 60°
=> ∠GBC = 120°/2 = 60°
∠GBC = ∠GCB = ∠BGC = 60°
$\therefore$ ΔGBC is equilateral triangle
Area of equilateral triangle = $\frac{\sqrt{3}}{4} * side^2$
Area of $\triangle$GBC = $\frac{\sqrt{3}}{4} * 8^2$
= 16$\sqrt{3}$
Median of triangle divides the triangle into two parts of equal area.
3 medians of a triangle divide the triangle into six parts of equal area.
$\therefore$ Area of ΔGBC = 2 × area of ΔGDC
Area of ΔABC = 6 × area of ΔGDC
= 3 × 2 × ΔGDC
= 3 × area of ΔGBC
= 3 × 16$\sqrt{3}$
= 48$\sqrt{3} cm^2$
8) Answer (D)
Floor area required for 5 persons = 16*5 = 80 $m^2$
Air space required for 5 persons = 100*5 = 500 $m^3$
Cone volume = $\frac{1}{3} \pi r^2h$
Let height be $h$
For smallest size, volume = 500 = $\frac{1}{3} * 80 * h$
=> $h = \frac{150}{8}$ = 18.75 m
9) Answer (B)
Let each side of the equilateral triangle be $a$
The altitude of an equilateral triangle bisects the opposite side.
=> $(\frac{a}{2})^2 + (12\sqrt{3})^2 = a^2$
=> $a^2 – \frac{a^2}{4} = 432$
=> $a^2 = \frac{1728}{3}$
Area of equilateral triangle = $\frac{\sqrt{3}}{4} * a^2$
= $\frac{\sqrt{3}}{4} * \frac{1728}{3}$
= $144\sqrt{3}$
10) Answer (B)
Let the side of equilateral triangle be ‘a’ units
the radius of circle be ‘r’ units.
and the side of square be ‘b’ units
Then,
Perimeter of square = 4b
Perimeter of equilateral triangle = 3a
Circumference of circle = $2*\pi*r$
Then acc to ques,
=> $4b = 3a = 2*\pi*r$
=> b = $\frac{\pi*r}{2}$
=> a = $\frac{2}{3} * \pi*r$
Now,
area of circle (C) = $\pi r^2$
area of equilateral triangle (T) = $\frac{\sqrt{3}}{4} * a^2$
=> area of equilateral triangle (T) =$\frac{\pi^2 * r^2}{3*\sqrt{3}}$
area of square (S) = b*b
=> area of square (S) = $\frac{\pi^2 r^2}{4}$
Hence it is clearly visible that C > S > T.
11) Answer (B)
Let radius of circle be $r$ and side of square be $a$
=> Circumference of circle = $2 \pi r = 44$
=> $r = 7 cm$
Since, the circular wire is bent to form square, => both of their perimeters are equal
=> Perimeter of square = $4a = 44$
=>$a = 11 cm$
Now, area of circular wire = $\pi r^2$
= $\frac{22}{7} * 7^2 = 154 cm^2$
Area of square = $a^2$
= $11^2 = 121 cm^2$
=> Required difference = 154-121 = $33 cm^2$
12) Answer (D)
Surface area of cone= $\frac{22}{7}\times r\times(r+L)$
where L=slant height
L= $\sqrt((r)^{2} + (h)^{2})$
Here when r=7 and h=24,
L= $\sqrt((7)^{2} + (24)^{2})$ = $\sqrt625$ = 25cm
Area, A= ${\frac{22}{7}}\times7\times(7+25)$
A= 704 $(cm)^{2}$
13) Answer (C)
Area of an equilateral triangle= $(\frac{\sqrt3}{4})\times(a)^{2}$
where a is side.
When a reduced to (a-2)
Area difference = 4${\sqrt3}$
$(\frac{\sqrt3}{4})$($(a)^{2}-(a-2)^{2})$= 4${\sqrt3}$
4a-4=16
a=5 (C)
14) Answer (C)
AD = 15 cm and ABC is equilateral triangle
In $\triangle$ADC
=> $tan \angle ACD = \frac{AD}{DC}$
=> $tan 60 = \frac{15}{DC}$
=> DC = $\frac{15}{\sqrt{3}} = 5\sqrt{3}$
=> BC = 2*DC = $10\sqrt{3}$
Area of $\triangle$ ABC = $\frac{\sqrt{3}}{4} * side^2$
= $\frac{\sqrt{3}}{4} * (10\sqrt{3})^2$
= $75\sqrt{3} cm^2$
15) Answer (B)
Let the radius be $x$. Since it is equal to the side of square
=> Side of square = $x$
Ratio of area of circle to that of square
= $\frac{\pi x^2}{x^2}$
= $\frac{\pi}{1}$
=> Required ratio = $\pi : 1$
16) Answer (C)
AD = 15 cm and ABC is equilateral triangle
In $\triangle$ADC
=> $tan \angle ACD = \frac{AD}{DC}$
=> $tan 60 = \frac{15}{DC}$
=> DC = $\frac{15}{\sqrt{3}} = 5\sqrt{3}$
=> BC = 2*DC = $10\sqrt{3}$
Area of $\triangle$ ABC = $\frac{\sqrt{3}}{4} * side^2$
= $\frac{\sqrt{3}}{4} * (10\sqrt{3})^2$
= $75\sqrt{3} cm^2$
17) Answer (D)
Let the side of square = $s$ cm and diagonal = $d$ cm
=> Area of square = $(s)^2 = 15\sqrt{3}$ ———-(i)
In right triangle of the square, => $(s)^2 + (s)^2 = (d)^2$
Substituting value of $s^2$ from equation (i)
=> $(d)^2 = 15\sqrt{3} + 15\sqrt{3} = 30\sqrt{3}$ ———-(ii)
Side of equilateral triangle = Diagonal of square = $d$ cm
$\therefore$ Area of equilateral triangle = $\frac{\sqrt{3}}{4} d^2$
Substituting value of $d^2$ from (ii), we get :
= $\frac{\sqrt{3}}{4} \times 30\sqrt{3} = \frac{90}{4} = \frac{45}{2} cm^2$
=> Ans – (D)
18) Answer (C)
Let the side of equilateral triangle = $a$ cm
Area of equilateral triangle = $\frac{\sqrt{3}}{4} a^2 = 9 \sqrt{3}$
=> $a^2 = 9 \times 4 = 36$
=> $a = \sqrt{36} = 6$ cm
The height $h$ of an equilateral triangle bisect the opposite side.
=> $(h)^2 = (6)^2 – (3)^2$
=> $(h)^2 = 36 – 9 = 27$
=> $h = \sqrt{27} = 3\sqrt{3}$ cm
=> Ans – (C)
19) Answer (B)
Let the side of square = $s$ cm and diagonal = $d$ cm
=> Area of square = $(s)^2 = 12$ ———-(i)
In right triangle of the square, => $(s)^2 + (s)^2 = (d)^2$
Substituting value of $s^2$ from equation (i)
=> $(d)^2 = 12 + 12 = 24$ ———-(ii)
Side of equilateral triangle = Diagonal of square = $d$ cm
$\therefore$ Area of equilateral triangle = $\frac{\sqrt{3}}{4} d^2$
Substituting value of $d^2$ from (ii), we get :
= $\frac{\sqrt{3}}{4} \times 24 = 6\sqrt{3} cm^2$
=> Ans – (B)
20) Answer (A)
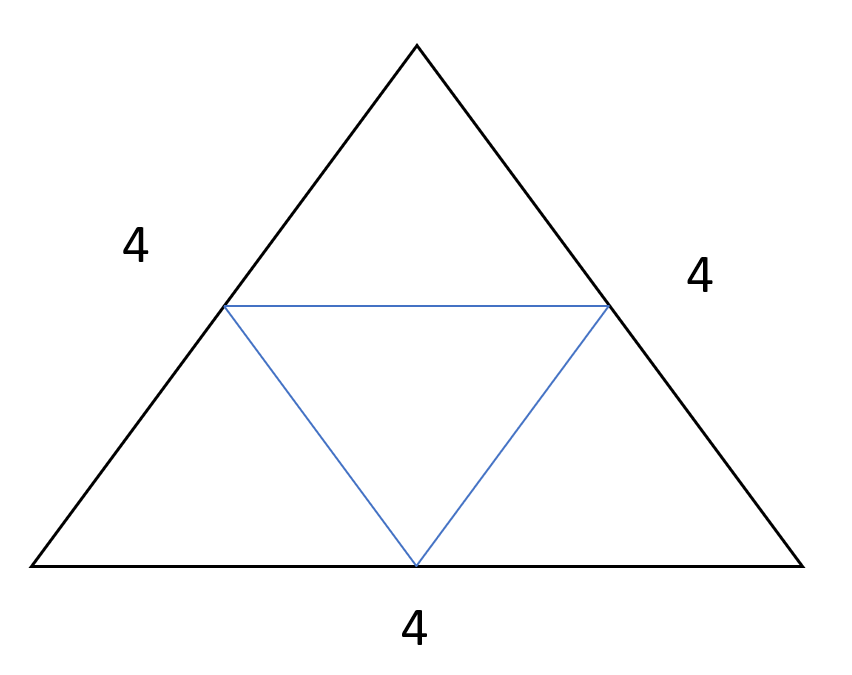
The area of the equilateral triangle = $\frac{\sqrt{3}}{4} * 4^2$ = $4\sqrt{3}$
The area of the triangle formed by joining the midpoints is one fourth the original triangle. Which is $\sqrt{3} $
Hence, the remaining area = $3 \sqrt{3}$
21) Answer (B)
We know that area of the equilateral triangle = $\frac{\sqrt{3}}{4}*s^2$
Therefore,
$\frac{81\sqrt{3}}{4}$ = $\frac{\sqrt{3}}{4}s^2$
=> s = 9 cm
We know that for an equilateral triangle, h = $\frac{\sqrt{3}}{2}$side
Therefore the required height is $4.5\sqrt{3}$ cm
22) Answer (A)
Let the side of square = $s$ cm and diagonal, $d=9$ cm
=> $(s)^2+(s)^2=(d)^2$
=> $2s^2=9^2=81$
=> $s^2=\frac{81}{2}$
=> $s=\sqrt{\frac{81}{2}} = \frac{9}{\sqrt{2}}$
Thus, perimeter of square = $4s$
= $4 \times \frac{9}{\sqrt{2}} = 18\sqrt{2}$ cm
Also, perimeter of square = Perimeter of equilateral triangle = $18\sqrt{2}$ cm
Let side of equilateral triangle = $a$ cm
=> $3a=18\sqrt{2}$
=> $a=\frac{18\sqrt{2}}{3} = 6\sqrt{2}$ cm
$\therefore$ Area of equilateral triangle = $\frac{\sqrt{3}}{4} a^2$
= $\frac{\sqrt{3}}{4} \times (6\sqrt{2})^2$
= $18\sqrt{3}$ $cm^2$
=> Ans – (A)
23) Answer (B)
Let the side of square = $s$ cm and diagonal = $d$ cm
=> Area of square = $(s)^2 = 6\sqrt{3}$ ———-(i)
In right triangle of the square, => $(s)^2 + (s)^2 = (d)^2$
Substituting value of $s^2$ from equation (i)
=> $(d)^2 = 6\sqrt{3} + 6\sqrt{3} = 12\sqrt{3}$ ———-(ii)
Side of equilateral triangle = Diagonal of square = $d$ cm
$\therefore$ Area of equilateral triangle = $\frac{\sqrt{3}}{4} d^2$
Substituting value of $d^2$ from (ii), we get :
= $\frac{\sqrt{3}}{4} \times 12\sqrt{3} = \frac{36}{4} = 9 cm^2$
=> Ans – (B)
24) Answer (D)
Side of an equilateral triangle, $a=6$ cm
Area = $\frac{\sqrt{3}}{4}(a)^2$
= $\frac{\sqrt{3}}{4} \times (6)^2 = \frac{36\sqrt{3}}{4}$
= $9\sqrt{3}$ $cm^2$
=> Ans – (D)
25) Answer (B)
Volume of the prism = area of base * height = $\sqrt{3} * 11^2$ * 4$\sqrt{3}$ / 4
= 121*3 = 363 cu. cm.
Hence, option B is the right answer.







