Important Questions of Geometry Circle for MAH-CET
Here you can download a free Geometry Circle questions PDF with answers for MAH MBA CET 2022 by Cracku. These are some tricky questions in the MAH MBA CET 2022 exam that you need to find the Geometry Circle of answers for the given questions. These questions will help you to make practice and solve the Geometry Circle questions in the MAH MBA CET exam. Utilize this best PDF practice set which is included answers in detail. Click on the below link to download the Geometry Circle MCQ PDF for MBA-CET 2022 for free.
Download Important Questions of Geometry Circle for MAH-CET
Enroll to MAH-CET 2022 Crash Course
Question 1: AB is the tangent on the circle at point A. The line BC meets the circle at points C and E. Line AD bisects the angle EAC. If angle EAC = $60^\circ$ and angle BAC : angle ACB = 2: 5. Find angle ABC :
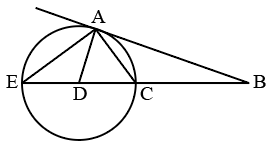
a) $40^\circ$
b) $60^\circ$
c) $30^\circ$
d) None of the options
1) Answer (A)
Solution:
Let us consider angle CAB=2x and angle ACB=5x
From Alternate segment theorem,
angle AEC = 2x
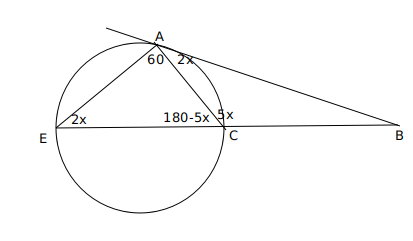
In triangle AEC, 60+180-5x+2x=180
3x=60
x=20
In triangle ABC, angle ABC = 180-7*20=40
A is the correct answer.
Question 2: Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
a) $\frac{1}{\surd2}$
b) $\frac{\pi}{3}$
c) $\surd2$
d) 1
2) Answer (D)
Solution:
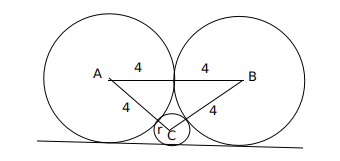
Let ‘h’ be the height of the triangle ABC, semiperimeter(S) $= \frac{4+4+r+4+4+r}{2} = 8+r$,
$a=4+r, b=4+r, c=8$
Area of triangle ABC $=\ \ \sqrt{\ s\cdot\left(s-a\right)\left(s-b\right)\left(s-c\right)}=$
$= \sqrt{\left(\ 8+r\right)\times\ 4\times\ 4\times\ r}$ = $\ \frac{\ 1}{2}\times\ \left(4+4\right)\times\ height$
Height (h) = $\sqrt{\ \left(8+r\right)r}$
Now, $ h + r = 4 \longrightarrow \sqrt{\ \left(8+r\right)r} + r = 4$ (Considering the height of the triangle)
$\sqrt{\ \left(8+r\right)r}$=4-r
16r=16
r=1
Alternatively,
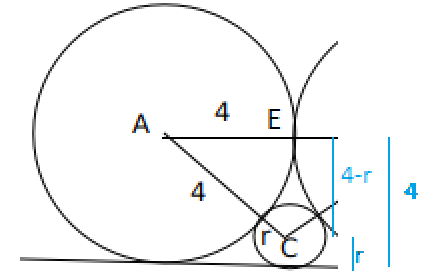
$\text{AE}^@+\text{EC}^2=\text{AC}^2 \longrightarrow 4^2+\left(4-r\right)^2 = \left(4+r\right)^2 \longrightarrow\ \longrightarrow\ \longrightarrow\ r=1$
Question 3: If two tangents inclined at an angle $60^\circ$ are drawn to a circle of radius 3 cm, then length of each tangent is equal to

a) $\frac{3}{2} \surd2 cm$
b) $6 cm$
c) $3 cm$
d) $3\surd3 cm$
3) Answer (D)
Solution:
TPO is a right angled triangle .
So $\sin\left(30\right)=\frac{OP}{TO}=\frac{3}{TO}\ =>TO=6$
$PT^2=TO^2-OP^2=36-9=27$
PT= 3$\sqrt{\ 3}$
Question 4: The radius of the incircle in the given diagram will be

a) 1.8 cm
b) 2 cm
c) 2.5 cm
d) 3.6 cm
4) Answer (B)
Solution:
AC= $\sqrt{\ AB^2\ +BC^2}=\ \sqrt{\ 6^2+8^2\ }=10$
In-radius of right angled triangle = $\frac{\left(a+b-h\right)}{2}$
Inradius = $\frac{\left(6+8-10\right)}{2}=2$
Question 5: As shown in the figure, there is a square of 24 cm. A circle is inscribed inside the square. Inside the circle are four circles of equal radius which are inscribed. The total area of the shaded region in the figure given below is ________

a) 576 – 196 $\pi$
b) 584 – 196 $\pi$
c) 864 – 196 $\pi$
d) none of the above
5) Answer (D)
Solution:
The above area can be obtained by the following operation: Area of Big Square – Area of the Bigger circle + $4\times\ $ Area of Smaller Circle + $8\times\ $ Overlapping Area of smaller circles
i) Area of Big Square = $24\times\ 24=576$
ii) Area of Big circle = $\pi\ 12^2\ =\ 144\pi\ $
iii) Area of smaller circle = $\pi\ 6^2\ =\ 36\pi\ $
iv) For Area of smaller common area = 2b from below figure
Area b = Area of circular arc(2b+a) – Area of triangle (a+b)
= $\frac{1}{4}\left(36\pi\ \right)-\ \frac{1}{2}\left(6\times\ 6\right)$ =$9\pi\ -18$
Area of common part of smaller circle = 2b = $18\pi\ -36$
Therefore required area = $576-144\pi+\left(4\times\ 36\pi\right)-8\times\ \left(18\pi\ -36\right)$
= $288+144\pi\ $
None of the above are correct
Take Free MAH-CET mock tests here
Enroll to 5 MAH CET Latest Mocks For Just Rs. 299
Question 6: Let $S_1$ be a square of side 4 cm. Circle $C_1$ circumscribes the square $S_1$ such that all its corners are on $C_1$. Another square $S_2$ circumscribes the circle $C_1$. Circle $C_2$ circumscribes the square $S_2$, and square $S_3$ circumscribes circle $C_2$, & so on. If $A_N$ is the area between the square $S_N$ and the circle $C_N$, where N is the natural number. then the ratio of sum of all $A_N$ to $A_l$ is
a) 1
b) $\frac{\pi}{2} – 1$
c) Can’t be determined
d) None of the above
6) Answer (D)
Solution:
Let the side of the square x be denoted by $S_x$
Let the radius of the circle y be denoted by $r_y$ and diameter by $d_y$
$S_{s1}=4$
$r_{c1}=\frac{d_{c1}}{2}=\frac{4\sqrt{\ 2}}{2}=2\sqrt{\ 2}$
$S_{s2}=d_{c1}=4\sqrt{\ 2}$
$r_{c2}=4$
..
.
.
A1 = $\pi\ r_{c1}^2-S_{s1}^2\ =\ 8\pi\ -16$
A2 = $16\pi\ -32$
A3 = $32\pi\ -64$
Sum = $\frac{\left(8\pi\ -16\right)\left(2^n-1\right)}{2-1}\ =\ \left(8\pi\ -16\right)\left(2^n-1\right)$
Ratio = $\left(2^n-1\right)$
Since the value of n is unknown, the answer can be C or D
Question 7: In the given figure, PA=QB and PRQ is the arc of the circle, centre of which is O such that angle POQ = 90°. If AB= 25$\sqrt{2}$cm and the perpendicular distance of AB from centre O is 30cm. Find the area of the shaded region?

a) $625\sqrt2$sq. cm
b) $625(\frac{1}{2} + \frac{\pi}{4})$sq. cm
c) $750\sqrt2- 625(\frac{1}{2} + \frac{\pi}{4})$sq. cm
d) None
7) Answer (C)
Solution:
PA = QB and A=B = $90^{\circ\ }$
=> PQBA is a rectangle.
Area of the shaded region = (Area of PQBA – Area of the segment PRQ)
$PQ=AB=25\sqrt{\ 5}$
$PO=QO=\frac{PQ}{\sqrt{\ 2}}=25$ = radius of the circle.
The perpendicular from O to PQ is $\frac{25}{\sqrt{\ 2}}$
Distance from the foot of the perpendicular to AB = $30-\frac{25}{\sqrt{\ 2}}$
Area of PQBA = $\left(30-\frac{25}{\sqrt{\ 2}}\right)\left(25\sqrt{\ 2}\right)=750\sqrt{\ 2}-625$
Area of segment PRQ = Area of sector OPRQ – Area of triangle OPQ = $\frac{90}{360}\pi\ 25^2-\frac{1}{2}25^2$
Area of shaded region = $\left(750\sqrt{\ 2}-625\right)-\left(\frac{90}{360}\pi\ 25^2-\frac{1}{2}25^2\right)$
= option C
Question 8: The point $R (4,10)$ lies on the curve $C: y = x^2 – 6x + 18.$ The tangent and normal to $C$ at $R$ meets the Y-axis at points $P$ and $Q$ respectively. A circle passes through the points $P,Q$ and $R$. The radius of this circle is
a) 3
b) 4
c) 5
d) 6
8) Answer (C)
Solution:
$\ \frac{\ dy}{dx}\ =\ 2x-6$
Slope of the tangent at R(4, 10) = 2
A normal will be perpendicular to tangent, so the slope of the normal = $\ \frac{\ -1}{2}$
Equation of the tangent at R(4, 10) =
y-10 = 2(x-4)
y=2x+2
The above line intersects Y-axis at P (0,2)
Equation of the normal at R(4, 10) =
y-10 = $\ \frac{\ -1}{2}$ (x-4)
2y=-x+24
The above line intersects Y-axis at Q (0,12)
Let the equation of the circle be $x^2+y^2+2gx+2fy+c=0$ with centre (-g, -f)
Now we have to find the equation of the circle passing through P (0, 2), Q(0, 12), R(4, 10)
On substituting these values in the equation of the circle, we get g = 0, f = -7, c = 24
Radii of the circle = $\sqrt{\ \left(g^2+f^2-c\right)}$
= 5
Question 9: Let the equations of two circles $C_1$ and $C_2$ be given by $x^2 + y^2 – 4x – 4y + 6 = 0$ and $x^2 + y^2 – 10x – 10y + k = 0$ respectively, where $k$ is a constant. Suppose that $C_1$ and $C_2$ have exactly two common tangents. Then possible values of $k$ are
a) $0 < k < 18$
b) $18 < k < 42$
c) $42 < k < 50$
d) none of the above
9) Answer (B)
Solution:
Centre and radius of a circle $x^2 + y^2 +2gx +2fy + c = 0$ is (-g,-h) and $\sqrt{g^{2}+h^{2}-c}$
Centre and the radius of $C_1$ is (2,2) and $\sqrt{2}$
Centre and the radius of $C_2$ is (5,5) and $\sqrt{50-k}$
Distance between the centres of the two circles = $\sqrt{18}$
According to the properties of the circle
If two circles have two common tangents then ,
|Difference of the radii| < Distance between the centres of the two circles < |Sum of the radii|
$\sqrt{50-k}$ – $\sqrt{2}$ < $\sqrt{18}$ < $\sqrt{50-k}$ + $\sqrt{2}$
Let’s look at the options one by one ,
Option A : let k= 1 |7-$\sqrt{2}$| < 3$\sqrt{2}$ < |7+$\sqrt{2}$| ——————-> Does not satisfy
Option B : let k= 25 |5-$\sqrt{2}$| < 3$\sqrt{2}$ < |5+$\sqrt{2}$| ——————-> Satisfied
Option C : let k= 49 |1-$\sqrt{2}$| < 3$\sqrt{2}$ < |1+$\sqrt{2}$| ——————-> Does not satisfy
Hence B is the correct answer.
Question 10: Let PQRS be a cycle quadrilateral. Let O be the centre of the circumcircle of the quadrilateral. Then which of the following statements is NOT true?
a) $\angle PRQ = \angle POQ$
b) $\angle POQ = 2\angle PSQ$
c) $\angle OPS = \angle OSP$
d) $\angle PRQ = \angle PSQ$
10) Answer (A)
Solution:

The angle which an arc of a circle subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.
$\angle\ POQ=2\angle\ PSQ$
Angles in the same segment of a circle are equal to one another
$\angle\ PRQ=\angle\ PSQ$
OPS is isosceles ( OP =OS =radius)
$\angle\ OPS=\angle\ OSP$
$\angle\ PRQ\ \ne\ \angle\ POQ$
Question 11: Two pairs of straight lines $x^2 — 7x + 6 = 0$ and $y^2 — 14y + 40 = 0$ intersect to form a rectangle. Let the diagonals of the rectangle intersect at the point W. A circle with center W and with tangents as lines $y^2 — 14y + 40 = 0$ intersects lines $x^2 — 7x + 6 = 0$ at points P, Q, R, S. The area of the rectangle PQRS is
a) $11\sqrt{15}$
b) $5\sqrt{11}$
c) $7\sqrt{11}$
d) $3\sqrt{5}$
11) Answer (B)
Solution:
$x^2 — 7x + 6 = 0$ => x= 1, x=6$PM\ =\sqrt{\ PW^2-MW^2}$
$y^2 — 14y + 40 = 0$ => y= 4, y=10

$W\ =\ \left(\frac{1+6}{2},\frac{4+10}{2}\right)\ =\ \left(\frac{7}{2},7\right)$
QR = 6-1 =5
r = (10-4)/2 = 3
PW = r= 3
MW = QR/2 = 5/2
$PM\ =\sqrt{\ PW^2-MW^2}$ = $\frac{\sqrt{\ 11}}{2}$
PQ=2PM = $\sqrt{\ 11}$
Area of PQRS = QR x PQ = $5\sqrt{\ 11}$
Question 12: The diameter of the circumcircle of the triangle formed by the line $24x + 7y =168$ and the coordinate axes is
a) $15\sqrt{2}$
b) $24$
c) $25$
d) $12\sqrt{3}$
12) Answer (C)
Solution:
Let’s rewrite the equation $24x + 7y =168$ in intercept form
$\frac{x}{7}+\frac{y}{24}$ = 1
$\therefore$ The co-ordinates of the triangle are (7,0),(0,0),(0,24)
Diameter of the circumcircle formed by the vertices is given by the hypotenuse, which is between (7,0) and (0,24).
Distance between the co-ordinates (7,0) and (0,24) =$\sqrt{7^{2} +24^{2}}$ =25.
Hence C is the correct answer.
Question 13: In the figure, PQ is a diameter of the circle. Angle PQS = $35^\circ$. Find angle QRS.

a) $55^\circ$
b) $45^\circ$
c) $35^\circ$
d) $60^\circ$
13) Answer (A)
Solution:

SInce PQ is the diameter, the angle subtended by it at R is 90 deg. i.e., $\angle$ PRQ = 90 deg.
Let $\angle$ RPQ = $\theta$, then $\angle$RQP = 90 – $\theta$
As the angles subtended by a chord in same segment are equal, $\angle$RPQ = $\angle$RSQ = $\theta$
In triangle RSQ, $\angle$QRS + $\angle$RSQ + $\angle$RQS = 180
$\Rightarrow$ $\angle$QRS + $\theta$ + 35 + 90 – $\theta$ = 180
$\Rightarrow$ $\angle$QRS = 180 – 125 = 55 deg.
Hence $\angle$QRS = 55 deg.
Question 14: In a circle of radius 6 cm, arc AB makes an angle of 114° with centre of the circle O.
What is angle ABO?
a) 23°
b) 42°
c) 38°
d) 33°
14) Answer (D)
Solution:
In $\triangle$AOB, AO = OB (Equal radii)
∴ $\triangle$AOB is isosceles.
∴ ∠ABO = ∠BAO = (180°-114°)/2 = 33°
Hence, option D.
Question 15: What is the maximum number of points that can be placed on a circular disk of radius 1 metre (some of the points could be placed on the bounding circle of the disk) such that no two points are at a distance of less than 1 metre from each other?
a) 6
b) 9
c) 7
d) 8
e) 5
15) Answer (C)
Solution:
In order to accommodate maximum number of points on the circular disk, all the points should be placed on the boundary of the disk as any point if placed inside the boundary would be less than 1 metre apart from the centre of the disk. Also, all the points have to be exactly 1 metre apart from each other to place maximum number of points. Hence, a maximum of 6 points can be placed on the boundary of the disk (each adjacent points placed 60 degrees apart) and 1 point at the centre.
Hence, a total of 7 points can be placed on the disk.
Question 16: Let C be a circle of radius $\sqrt{20}$ cm. Let L1, L2 be the lines given by 2x − y −1 = 0 and x + 2y−18 = 0, respectively. Suppose that L1 passes through the center of C and that L2 is tangent to C at the point of intersection of L1 and L2. If (a,b) is the center of C, which of the following is a possible value of a + b?
a) 11
b) 17
c) 8
d) 20
e) 14
16) Answer (B)
Solution:
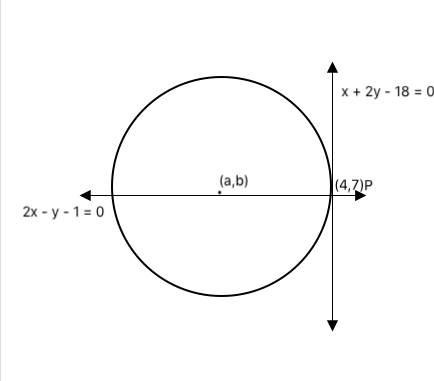
As mentioned in the question,
Lines L1 and L2 intersect at point P as shown in the figure.
On solving for x and y from equations
x + 2y – 18 = 0
2x – y – 1 = 0
We get x = 4 and y =7.
Given, radius = $\sqrt{20}$
Using the equation of a circle, we have
$(4-a)^{2}$ + $(7-b)^{2}$ = 20….(1)
The center of the circle will lie on the line: 2x – y – 1 = 0
a,b will satisfy this equation.
So 2a-b-1=0
b=2a-1
From equation 1…
$(4-a)^{2}$ + $(7-b)^{2}$ = 20
$(4-a)^{2}$ + $(8-2a)^{2}$ = 20
5$(4-a)^{2}$ = 20
a=6 or a=2
b=11 or b=3
The sum of the coordinates possible=6+11 or 2+3
i.e. 17 or 5
Option B is one of the solution.
Question 17: On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is
17) Answer: 24
Solution:
Let us draw the diagram according to the available information.
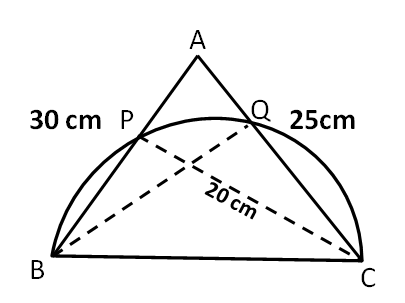
We can see that triangle BPC and BQC are inscribed inside a semicircle. Hence, we can say that
$\angle$ BPC = $\angle$ BQC = 90°
Therefore, we can say that BQ $\perp$ AC and CP $\perp$ AB.
In triangle ABC,
Area of triangle = (1/2)*Base*Height = (1/2)*AB*CP = (1/2)*AC*BQ
$\Rightarrow$ BQ = $\dfrac{AB*CP}{AC}$ = $\dfrac{30*20}{25}$ = 24 cm.
Question 18: A chord of length 5 cm subtends an angle of 60° at the centre of a circle. The length, in cm, of a chord that subtends an angle of 120° at the centre of the same circle is
a) $5\sqrt{3}$
b) $2\pi$
c) $8$
d) $6\sqrt{2}$
18) Answer (A)
Solution:
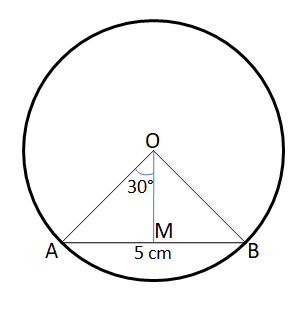
We are given that AB = 5 cm and $\angle$ AOB = 60°
Let us draw OM such that OM $\perp$ AB.
In right angle triangle AMO,
$sin 30° = \dfrac{AM}{AO}$
$\Rightarrow$ AO = 2*AM = 2*2.5 = 5 cm. Therefore, we can say that the radius of the circle = 5 cm.
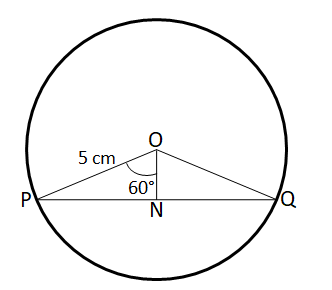
In right angle triangle PNO,
$sin 60° = \dfrac{PN}{PO}$
$\Rightarrow$ PN = $\dfrac{\sqrt{3}}{2}$*PO = $\dfrac{5\sqrt{3}}{2}$
Therefore, PQ = 2*PN = $5\sqrt{3}$ cm
Question 19: In a circle with center O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
a) $ (\frac{\pi}{4\sqrt{3}})^{\frac{1}{2}}$
b) $(\frac{\pi}{6})^{\frac{1}{2}}$
c) $(\frac{\pi}{3\sqrt{3}})^{\frac{1}{2}}$
d) $(\frac{\pi}{4})^{\frac{1}{2}}$
19) Answer (C)
Solution:
It is given that radius of the circle = 1 cm
Chord AB subtends an angle of 60° on the centre of the given circle. R be the region bounded by the radii OA, OB and the arc AB.
Therefore, R = $\dfrac{60°}{360°}$*Area of the circle = $\dfrac{1}{6}$*$\pi*(1)^2$ = $\dfrac{\pi}{6}$ sq. cm
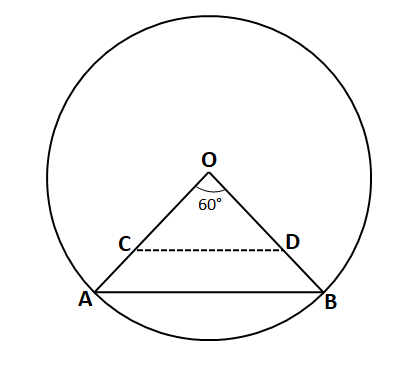
It is given that OC = OD and area of triangle OCD is half that of R. Let OC = OD = x.
Area of triangle COD = $\dfrac{1}{2}*OC*OD*sin60°$
$\dfrac{\pi}{6*2}$ = $\dfrac{1}{2}*x*x*\dfrac{\sqrt{3}}{2}$
$\Rightarrow$ $x^2 = \dfrac{\pi}{3\sqrt{3}}$
$\Rightarrow$ $x$ = $(\frac{\pi}{3\sqrt{3}})^{\frac{1}{2}}$ cm. Hence, option C is the correct answer.
Question 20: Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?
a) 24, 10
b) 25, 9
c) 25, 10
d) 24, 12
20) Answer (A)
Solution:
Let ABCD be a rectangle inscribed in a circle of radius 13 cm. Which one of the following pairs can represent, in cm, the possible length and breadth of ABCD?
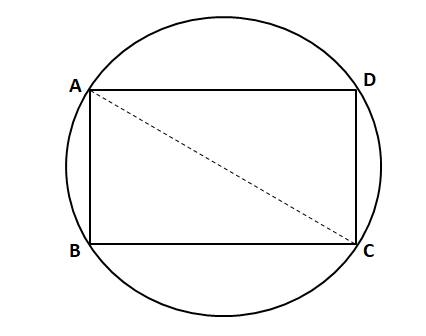
We know that AC is the diameter and $\angle$ ABC = 90°. AC = 2*13 = 26 cm
In right angle triangle ABC,
$AC^2 = AB^2 + BC^2$
$\Rightarrow$ $AB^2+BC^2=26^2$
$\Rightarrow$ $AB^2+BC^2=676$
Let us check with the options.
Option (A): $24^2+10^2 = 676$. Hence, this is a possible answer.
Option (B): $25^2+9^2 = 706 \neq 676$. Hence, this is an incorrect pair.
Option (C): $25^2+10^2 = 725 \neq 676$. Hence, this is an incorrect pair.
Option (D): $24^2+12^2 = 720 \neq 676$. Hence, this is an incorrect pair.
Therefore, we can say that option A is the correct answer.






