CAT Geometry Triangle Questions PDF [Most Important]

Geometry is one of the most important topics in the CAT Quantitative Ability (QA) section. Many aspirants try to avoid this section assuming it’s tough. But remember that Geometry can be improved with more practice. If you’re weak in Geometry check out this Important Formula Sheet of Geometry PDF. Triangles is one of the key topics in CAT Geometry. Every year questions are asked on Geometry Triangles. You can check out these Geometry Triangle-based questions from CAT Previous year’s papers. Practice a good number of sums on CAT Geometry Triangle questions so that you don’t miss out on the easy questions from this topic. In this article, we will look into some important Geometry Triangle Questions for CAT Quants. These are a good source for practice; If you want to practice these questions, you can download this CAT Geometry Triangle Questions PDF below, which is completely Free.

Download Geometry Triangle Questions for CAT

Enroll for CAT 2022 Online Course

Looking for hardcopy of CAT Previous Papers?

Order below. Delivery charges are on us 🙂

Question 1: In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?

a) 17.05

b) 27.85

c) 22.45

d) 32.25

e) 26.25

1) Answer (E)

View Video Solution

Solution:

Let x be the value of third side of the triangle. Now we know that Area = 17.5*9*x/(4*R), where R is circumradius.

Also Area = 0.5*x*3 .

Equating both, we have 3 = 17.5*9 / (2*R)

=> R = 26.25.

Question 2: Consider obtuse-angled triangles with sides 8 cm, 15 cm and x cm. If x is an integer then how many such triangles exist?

a) 5

b) 21

c) 10

d) 15

e) 14

2) Answer (C)

View Video Solution

Solution:

For obtuse-angles triangle, $c^2 > a^2 + b^2$ and c < a+b
If 15 is the greatest side, 8+x > 15 => x > 7 and $225 > 64 + x^2$ => $x^2$ < 161 => x <= 12
So, x = 8, 9, 10, 11, 12
If x is the greatest side, then 8 + 15 > x => x < 23
$x^2 > 225 + 64 = 289$ => x > 17
So, x = 18, 19, 20, 21, 22
So, the number of possibilities is 10

Question 3: In triangle DEF shown below, points A, B and C are taken on DE, DF and EF respectively such that EC = AC and CF = BC. If angle D equals 40 degress , then angle ACB is ?

a) 140

b) 70

c) 100

d) None of these

3) Answer (C)

View Video Solution

Solution:

Let angle EAC = x, so angle AEC = x and angle ACE = 180-2x
Let angle FBC = y, so angle BFC = y and angle BCF = 180-2y
So, angle ACB = 180-(180-2x+180-2y) = 2(x+y) – 180
x+y = 180 – 40 = 140
So, angle ACB = 280 – 180 = 100

Question 4: If a,b,c are the sides of a triangle, and $a^2 + b^2 +c^2 = bc + ca + ab$, then the triangle is:

a) equilateral

b) isosceles

c) right angled

d) obtuse angled

4) Answer (A)

View Video Solution

Solution:

$(a+b+c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca) => 3(a^2 + b^2 + c^2)$

This is possible only if a = b = c.

So, the triangle is an equilateral triangle.

Question 5: The area of the triangle whose vertices are (a,a), (a + 1, a + 1) and (a + 2, a) is
[CAT 2002]

a) $a^3$

b) $1$

c) $2a$

d) $2^{1/2}$

5) Answer (B)

View Video Solution

Solution:

The triangle we have is :

The length of three sides is $\sqrt 2, \sqrt 2$ and $2$.
This is a right-angled triangle.
Hence, it’s area equals $1/2 * \sqrt 2 * \sqrt 2 = 1$
So, the correct answer is b)
Alternate Approach :
Area of triangle = $\frac{1}{2}\times\ base\times\ height$
So we get $\frac{1}{2}\times2\times\ 1$=1 square units

Checkout: CAT Free Practice Questions and Videos

Question 6: In the following figure, ACB is a right-angled triangle. AD is the altitude. Circles are inscribed within the triangle ACD and triangle BCD. P and Q are the centres of the circles. The distance PQ is

The length of AB is 15 m and AC is 20 m

a) 7 m

b) 4.5 m

c) 10.5 m

d) 6 m

6) Answer (A)

View Video Solution

Solution:

By Pythagoras theorem we get BC = 25 . Let BD = x;Triangle ABD is similar to triangle CBA => AD/15 = x/20 and also triangle ADC is similar to triangle ACB=> AD/20 = (25-x)/15. From the 2 equations, we get x = 9 and DC = 16

We know that AREA = (semi perimeter ) * inradius

For triangle ABD, Area = 1/2 x BD X AD = 1/2 x 12 x 9 = 54 and semi perimeter = (15 + 9 + 12)/2 = 18. On using the above equation we get, inradius, r = 3.

Similarly for triangle ADC we get inradius R = 4 .

PQ = R + r = 7 cm

Question 7: If ABCD is a square and BCE is an equilateral triangle, what is the measure of ∠DEC?

a) 15°

b) 30°

c) 20°

d) 45°

7) Answer (A)

View Video Solution

Solution:

According to given diagram, as triangle BCE is equilateral CE=BE=DC
Hence angle CDE = angle CED

So angle DEC = $\frac{180-150}{2} = 15$
Question 8: In triangleABC, ∠B is a right angle, AC = 6 cm, and D is the mid-point of AC. The length of BD is

a) 4cm

b) 6 cm

c) 3cm

d) 3.5cm

8) Answer (C)

View Video Solution

Solution:

A circle is circumscribed to triangle ABC.

For this circle D will be centre of circle, and AD , DC , BD will radius of this circle.

Hence AD=BD=DC=3 cm

Question 9: From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is

a) $225\sqrt{3}$

b) $\frac{500}{\sqrt{3}}$

c) $\frac{275}{\sqrt{3}}$

d) $\frac{250}{\sqrt{3}}$

9) Answer (B)

View Video Solution

Solution:

The lengths are given as 40, 25 and 35.

The perimeter = 100

Semi-perimeter, s = 50

Area = $ \sqrt{50 * 10 * 25 * 15}$ = $250\sqrt{3}$

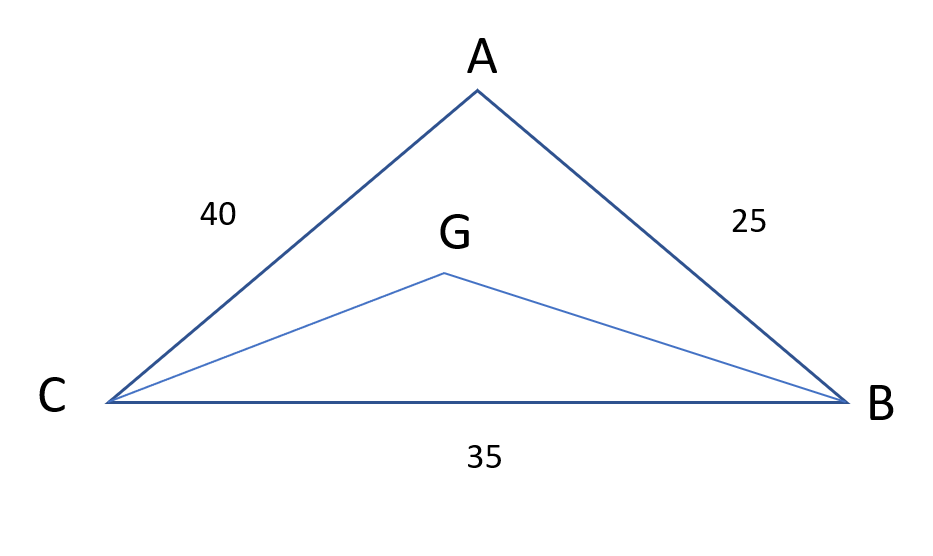
The triangle formed by the centroid and two vertices is removed.

Since the cenroid divides the median in the ratio 2 : 1

The remaining area will be two-thirds the area of the original triangle.

Remaining area = $\frac{2}{3} * 250\sqrt{3}$ = $\frac{500}{\sqrt{3}}$

Question 10: Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is

10) Answer: 24

View Video Solution

Solution:

The length of the altitude from A to the hypotenuse will be the shortest distance.

This is a right triangle with sides 3 : 4 : 5.

Hence, the hypotenuse = $\sqrt{20^2+15^2}$ = 25 Km.

Length of the altitude = $\frac{15 * 20}{25}$ = 12 Km

(This is derived from equating area of triangle, $\frac{15\cdot20}{2}\ =\ \frac{25\cdot\text{altitude}}{2}$)

The time taken = $\frac{12}{30} * 60$ = 24 minutes

CAT Geometry Preparation Videos | CAT 2022 Preparation Videos