Geometry Questions for XAT
Download important Geometry Questions for XAT PDF based on previously asked questions in the XAT exam. Practice Geometry Questions PDF for the XAT exam.
Download Geometry Questions for XAT
Get 5 XAT mocks for Rs. 299. Enroll here
Question 1: Three horses are grazing within a semi-circular field. In the diagram given below, AB is the diameter of the semi-circular field with center at O. Horses are tied up at P, R and S such that PO and RO are the radii of semi-circles with centers at P and R respectively, and S is the center of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi-circles and the horse tied at S can graze within the circle centred at S. The percentage of the area of the semi-circle with diameter AB that cannot be grazed by the horses is nearest to

a) 20
b) 28
c) 36
d) 40
Question 2: In the figure below, AB is the chord of a circle with center O. AB is extended to C such that BC = OB. The straight line CO is produced to meet the circle at D. If $\angle{ACD}$ = y degrees and $\angle{AOD}$ = x degrees such that x = ky, then the value of k is

a) 3
b) 2
c) 1
d) None of the above.
Question 3: If the lengths of diagonals DF, AG and CE of the cube shown in the adjoining figure are equal to the three sides of a triangle, then the radius of the circle circumscribing that triangle will be?
a) equal to the side of the cube
b) $\sqrt 3$ times the side of the cube
c) 1/$\sqrt 3$ times the side of the cube
d) impossible to find from the given information
Question 4: A circle with radius 2 is placed against a right angle. Another smaller circle is also placed as shown in the adjoining figure. What is the radius of the smaller circle?

a) $3 – 2 \sqrt{2}$
b) $4 – 2 \sqrt{2}$
c) $7- 4 \sqrt{2}$
d) $6- 4 \sqrt{2}$
Question 5: 
In the adjoining figure, chord ED is parallel to the diameter AC of the circle. If angle CBE = 65°, then what is the value of angle DEC?
a) 35
b) 55
c) 45
d) 25
Question 6: The figure shows a circle of diameter AB and radius 6.5 cm. If chord CA is 5 cm long, find the area of triangle ABC.

a) 60 sq. cm
b) 30 sq. cm
c) 40 sq. cm
d) 52 sq. cm
Question 7: 
AB is the diameter of the given circle, while points C and D lie on the circumference as shown. If AB is 15 cm, AC is 12 cm and BD is 9 cm, find the area of the quadrilateral ACBD.
a) 54sq. cm
b) 216sq. cm
c) 162sq. cm
d) None of these
Question 8: In the adjoining figure, points A, B, C and D lie on the circle. AD = 24 and BC = 12. What is the ratio of the area of CBE to that of ADE?

a) 1 : 4
b) 1 : 2
c) 1 : 3
d) Data insufficient
Question 9: Three circles, each of radius 20, have centres at P, Q and R. Further, AB = 5, CD = 10 and EF = 12. What is the perimeter of ΔPQR ?

a) 120
b) 66
c) 93
d) 87
Question 10:
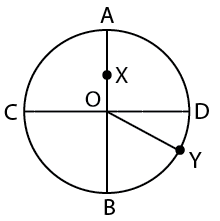
In a circular field, AOB and COD are two mutually perpendicular diameters having length of 4 meters. X is the mid – point of OA. Y is the point on the circumference such that ∠YOD = 30°. Which of the following correctly gives the relation among the three alternate paths from X to Y?
a) XOBY : XODY : XADY :: 5.15 : 4.50 : 5.06
b) XADY : XODY : XOBY :: 6.25 : 5.34 : 4.24
c) XODY : XOBY : XADY :: 4.04 : 5.35 : 5.25
d) XADY : XOBY : XODY :: 5.19 : 5.09 : 4.04
e) XOBY : XADY : XODY :: 5.06 : 5.15 : 4.50
XAT Decision making practice questions
Answers & Solutions:
1) Answer (B)
Let R be radius of big circle and r be radius of circle with centre S. Radius of 2 semicircles is R/2.
From Right angled triangle OPS, using pythagoras theorem we get
$(r+0.5R)^2 = (0.5R)^2 + (R-r)^2$ . We get R=3r .
Now the area of big semicircle that cannot be grazed is Area of big S.C – area of 2 semicircle – area of small circle = $\pi*R^2$/2 – 2*$\pi*(0.5R)^2$/2-$\pi*r^2$ = $\pi*R^2$/2 – 2*$\pi*(0.5R)^2$/2-$\pi*(R/3)^2$= $\pi*R^2$/2 – $\pi*(R)^2$/4-$\pi*(R)^2$/9 = 5*$\pi*R^2$/36. this is about 28 % of the area $\pi*R^2$/2 . Hence option B.
2) Answer (A)
Since Angle BOC = Angle BCO = y.
Angle OBC = 180-2y .
Hence Angle ABO = z = 2y = Angle OAB.
Now since x is exterior angle of triangle AOC .
We have x = z + y = 3y.
Hence option A.
3) Answer (A)
Consider side of the cube as x.
So diagonal will be of length $\sqrt{3}$ * x.
Now if diagonals are side of equilateral triangle we get area = 3*$\sqrt{3}*x^2$ /4 .
Also in a triangle
4 * Area * R = Product of sides
4* 3*$\sqrt{3}*x^2$ /4 * R = .3*$\sqrt{3}*x^3$
R = x
4) Answer (D)

Using pythagoras we can find diagonal of small square shown in fig. = 2*$\sqrt2$ . Now this is equal to 2 + r + $\sqrt2$ *r. Equating we get r = $6- 4 \sqrt{2}$
5) Answer (D)
If EBC = 65 then EOC = 130 then OEC = OCE = 25. NOw since OC and ED are parallel we have OCE = OED = 25. Hence option D.
6) Answer (B)
According to given dimensions, triangle will be a right angled triangle.
So BC = 12
And area = $\frac{1}{2} \times 12 \times 5$
= 30
7) Answer (D)
Since ACBD is cyclic quadrilateral with diagonals as AB = 15 ad CD.
So area = $\frac{1}{2} \times (AB) \times (CD)$ eq.(1)
Triangle ACB and ABD is right angled triangle
Let’s say angle CBA = $\theta$
so $CD = 2 \times (9 sin\theta)$ (Where $sin\theta$ = $\frac{12}{15}$)
CD = $\frac{72}{5}$
Putting values in eq. (1) , we will get area = 108 sq.cm.
Hence answer will be D)
8) Answer (A)
As we know angles of same sectors are equal
Hence angle B and angle D will be equal. Angle BCE and angle EAD will be equal.
So triangles BCE and EAD will be similar triangles with sides ratio as 12:24 or 1:2.
Area will be in ratio of 1:4.
9) Answer (C)
As radius of circle is 20, lengths of PR, QR and PQ will be (15+5+15) , (10+10+10) , (8+12+8) respectively.
So perimeter will be = 28 + 30 + 35 = 93
10) Answer (D)
XADY = XA + AD + DY = 2/2 + (2 * 3.14 * 2)/4 + (30/360) * (2 * 3.14 * 2) = 5.19
XOBY = XO + OB + BY = 2/2 + 2 + (60/360) * (2 * 3.14 * 2) = 5.09
XODY = XO + OD + DY = 2/2 + 2 + (30/360) * (2 * 3.14 * 2) = 4.04
Hence, option D is the correct answer.
We hope this Geometry QuestionsN PDF for XAT with Solutions will be helpful to you.







![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
