Geometry Questions for TISSNET 2022 – Download PDF

Download TISSNET 2022 Geometry [PDF] by Cracku. Very Important Geometry Questions for TISSNET 2022 based on asked questions in previous exam papers. These questions will help your TISSNET exam preparation. So kindly download the PDF for reference and do more practice.

Download Geometry Questions for TISSNET

Get 5 TISSNET mocks at just Rs.299

Download TISSNET previous papers PDF

Question 1: ABC is a triangle with integer-valued sides AB = 1, BC >1, and CA >1. If D is the mid-point of AB, then, which of the following options is the closest to the maximum possible value of the angle ACD (in degrees)?

a) 15

b) 30

c) 45

d) 75

e) 60

Question 2: The six faces of a wooden cube of side 6 cm are labelled A, B, C, D, E and F respectively. Three of these faces A, B, and C are each adjacent to the other two, and are painted red. The other three faces are not painted. Then, the wooden cube is neatly cut into 216 little cubes of equal size. How many of the little cubes have no sides painted?

a) 125

b) 135

c) 91

d) 108

e) 100

Question 3: The point $R (4,10)$ lies on the curve $C: y = x^2 – 6x + 18.$ The tangent and normal to $C$ at $R$ meets the Y-axis at points $P$ and $Q$ respectively. A circle passes through the points $P,Q$ and $R$. The radius of this circle is

a) 3

b) 4

c) 5

d) 6

Question 4: An equilateral triangle, having each side as a , has its corners cut away so as to form a regular hexagon. The area of the hexagon is

a) $\frac{\sqrt3 a^2}{6}$

b) $\frac{2\sqrt3 a^2}{3}$

c) $\frac{\sqrt3 a^2}{12}$

d) $\frac{\sqrt3 a^2}{4}$

Question 5: What is the sum of the interior angles at the vertices of a 5-pointed star as shown below? The star need not have sides of the same length.

a) 120°

b) 180°

c) 540°

d) depends on the sides of the star.

Download TISSNET Previous Papers PDF

Question 6: A bucket contains 200cc of liquid. A solid ball is dropped in the bucket resulting in the rise of liquid level to 1.3 times of its original level. If the radius of the base of the bucket is 3 cm and the radius of the surface of the liquid level is 1 cm more than the radius of the base of the bucket before the ball is dropped. Find the volume of the solid metal ball.

a) 68cc

b) 80cc

c) 92cc

d) Can’t be determined

Question 7: In the triangle PQR, S is the midpoint of QR. X is any point on PR. T is the point on QR such that PT || SX. If the area of triangle PQR is 5.8 sq. cm. then the area of triangle RTX is

a) 2.9 sq. cm

b) 3.2 sq. cm

c) 5.8 sq. cm

d) 2.45 sq. cm

Question 8: Let $S_1$ be a square of side 4 cm. Circle $C_1$ circumscribes the square $S_1$ such that all its corners are on $C_1$. Another square $S_2$ circumscribes the circle $C_1$. Circle $C_2$ circumscribes the square $S_2$, and square $S_3$ circumscribes circle $C_2$, & so on. If $A_N$ is the area between the square $S_N$ and the circle $C_N$, where N is the natural number. then the ratio of sum of all $A_N$ to $A_l$ is

a) 1

b) $\frac{\pi}{2} – 1$

c) Can’t be determined

d) None of the above

Question 9: As shown in the figure, there is a square of 24 cm. A circle is inscribed inside the square. Inside the circle are four circles of equal radius which are inscribed. The total area of the shaded region in the figure given below is ________

a) 576 – 196 $\pi$

b) 584 – 196 $\pi$

c) 864 – 196 $\pi$

d) none of the above

Question 10: The radius of the incircle in the given diagram will be

a) 1.8 cm

b) 2 cm

c) 2.5 cm

d) 3.6 cm

Question 11: C is the mid-point of PQ, if P is (4, x), C is (y, -1) and Q is (-2, 4), then x and y respectively are

a) -6 and 1

b) -6 and 2

c) 6 and -1

d) 6 and -2

Question 12: In the adjoining figure, ABCD is a cyclic quadrilateral. If AB is a diameter, BC = CD and $\angle ABD = 40^\circ$, find the measure of $\angle DBC$.

a) 65

b) 25

c) 45

d) 60

Question 13: In the triangle ABC, MN is parallel to AB. Area of trapezium ABNM is twice the area of triangle CMN. What is ratio of CM : AM ?

a) $\frac{1}{(\surd3 + 1)}$

b) $\frac{(\surd3 – 1)}{2}$

c) $\frac{(\surd3 + 1)}{2}$

d) none of these

Question 14: If ABCD is a square and BCE is an equilateral triangle, what is the measure of the angle DEC?

a) $15^\circ$

b) $30^\circ$

c) $20^\circ$

d) $45^\circ$

Question 15: A rectangular park 60 m long and 40 m wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 sq. m, then what is the width of the road?

a) 2.91 m

b) 3 m

c) 5.82 m

d) None of these

Question 16: A solid sphere is melted and recast into a right circular cone with a base radius equal to the radius of the sphere. What is the ratio of the height and radius of the cone so formed?

a) 4 : 3

b) 2 : 3

c) 3 : 4

d) None of these

Question 17: Consider a cuboidal underground tunnel of length 500 m whose cross-section is given in the figure. If $1 m^3$ of concrete costs 1000 rupees, find the amount of money needed to build the Tunnel.

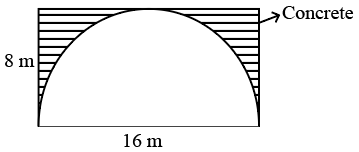
a) $8(4-\pi)10^6 $ rupees

b) $64(4-\pi)10^6 $ rupees

c) $16(4-\pi)10^6 $ rupees

d) $32(4-\pi)10^6 $ rupees

Question 18: In the quadrilateral $ABCD$ below, $\angle DAB$ = 90° and $AB = 24$cm , $BC = 40$cm, $CD = 50$cm and $AD = 18$cm(The diagram is not drawn to scale) Find the area of the quadrilateral

a) 1089 $cm^2$

b) 914 $cm^2$

c) 816 $cm^2$

d) 726 $cm^2$

Question 19: Normals to the parabola $y^2 = 4x$ are drawn at two points P and Q on it. These normals intersect the parabola at the point R (9, -6). Then PQ equals

a) $\sqrt{13}$

b) $\sqrt{15}$

c) $\sqrt{17}$

d) $\sqrt{21}$

Question 20: Two pairs of straight lines $x^2 — 7x + 6 = 0$ and $y^2 — 14y + 40 = 0$ intersect to form a rectangle. Let the diagonals of the rectangle intersect at the point W. A circle with center W and with tangents as lines $y^2 — 14y + 40 = 0$ intersects lines $x^2 — 7x + 6 = 0$ at points P, Q, R, S. The area of the rectangle PQRS is

a) $11\sqrt{15}$

b) $5\sqrt{11}$

c) $7\sqrt{11}$

d) $3\sqrt{5}$

Take TISSNET Mock Tests

Answers & Solutions:

1) Answer (A)

We will try to maximize the value of the angle ACD:

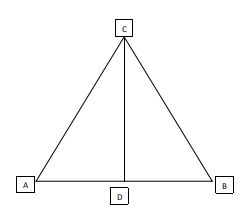
For a fixed triangle ABC, the angle ACD can be maximized when we take the median CD to be perpendicular to AB and the value of AC is as small as possible, so that the sine of angle ACD, and hence, the angle ACD itself if maximized, as the value of AD is fixed at half of AB at 0.5.

Now, the least possible value of AC is 2. The triangle will be of sides (1,2,2).

Value of sin(ACD)=$\frac{0.5}{2}=0.25$

$\angle\ ACD=\sin^{-1}\left(0,25\right)=14.78\approx\ 15.$

2) Answer (A)

Since A, B and C are adjacent faces. If we remove them, the resultant solid will also be a cube with side 5.

Hence total number of cubes unpainted = $5^3$ = 125

3) Answer (C)

$\ \frac{\ dy}{dx}\ =\ 2x-6$

Slope of the tangent at R(4, 10) = 2

A normal will be perpendicular to tangent, so the slope of the normal = $\ \frac{\ -1}{2}$

Equation of the tangent at R(4, 10) =

y-10 = 2(x-4)

y=2x+2

The above line intersects Y-axis at P (0,2)

Equation of the normal at R(4, 10) =

y-10 = $\ \frac{\ -1}{2}$ (x-4)

2y=-x+24

The above line intersects Y-axis at Q (0,12)

Let the equation of the  circle be $x^2+y^2+2gx+2fy+c=0$ with centre (-g, -f)

Now we have to find the equation of the circle passing through P (0, 2), Q(0, 12), R(4, 10)

On substituting these values in the equation of the circle, we get g = 0, f = -7, c = 24

Radii of the circle = $\sqrt{\ \left(g^2+f^2-c\right)}$

= 5

4) Answer (A)

To make a regular hexagon, three equilateral triangles of side$\ \frac{\ a}{3}$ will be cut from the corners to make a regular hexagon of side a.

Hence, this hexagonal can be further divided into 6 equilateral triangles of side $\ \frac{\ a}{3}$.

Hence the area of the hexagon = $\ 6\cdot\ \frac{\ \sqrt{\ 3}}{4}$*($\ \ \frac{\ a}{3}$)$^2$ = $\frac{\sqrt3 a^2}{6}$

A is the answer.

5) Answer (B)

In triangle AFJ, $x_{1}$+180-a+180-b=180

=> $x_{1}$+180=a+b

Similarly, $x_{2}$+180=a+e

$x_{3}$+180=d+e

$x_{4}$+180=c+d

$x_{5}$+180=b+c

Adding all the equations,

$x_{1}$+$x_{2}$+$x_{3}$+$x_{4}$+$x_{5}$+180*5= 2(a+b+c+d+e)

=> Sum of interior angles = 2*(a+b+c+d+e)-900  = 2*540-900=180   (Sum of interior angles of a pentagon = 540)

6) Answer (B)

Let height of liquid level before the ball was dropped be h

The radius of the surface of the liquid level then is 4cm

$\frac{h}{3}\pi\ \left(4^2+3^2+4\cdot3\right)\ =200cc$

=> h = $\frac{600}{37\pi\ }$

The liquid level raises by 0.3h as a result of the solid metal ball being dropped.

By similarity, the radius of the surface of the liquid level after metal ball is dropped is 4.3cm

Volume of he solid metal ball = $\frac{1.3h}{3}\left(4^2+3^2+4.3\left(3\right)\right)\ -\ 200$ = 83.82cc

7) Answer (A)

S is the midpoint of QR. So, area of PSR = $\frac{1}{2}\left(Area\ of\ PQR\right)\ =\ \frac{5.8}{2}=2.9$

PT||XS

So area of XSP = area of XST ( same height and same base)

Adding area of XSR on both sides, we have area of PSR = Area of RTX

=>  area of PSR = Area of RTX = 2.9 sq.cm

8) Answer (D)

Let the side of the square x be denoted by $S_x$

Let the radius of the circle y be denoted by $r_y$ and diameter by $d_y$

$S_{s1}=4$

$r_{c1}=\frac{d_{c1}}{2}=\frac{4\sqrt{\ 2}}{2}=2\sqrt{\ 2}$

$S_{s2}=d_{c1}=4\sqrt{\ 2}$

$r_{c2}=4$

..

.

.

A1 = $\pi\ r_{c1}^2-S_{s1}^2\ =\ 8\pi\ -16$

A2 = $16\pi\ -32$

A3 = $32\pi\ -64$

Sum = $\frac{\left(8\pi\ -16\right)\left(2^n-1\right)}{2-1}\ =\ \left(8\pi\ -16\right)\left(2^n-1\right)$

Ratio = $\left(2^n-1\right)$

Since the value of n is unknown, the answer can be C or D

9) Answer (D)

The above area can be obtained by the following operation: Area of Big Square – Area of the Bigger circle + $4\times\ $ Area of Smaller Circle + $8\times\ $ Overlapping Area of smaller circles

i) Area of Big Square = $24\times\ 24=576$

ii) Area of Big circle = $\pi\ 12^2\ =\ 144\pi\ $

iii) Area of smaller circle = $\pi\ 6^2\ =\ 36\pi\ $

iv) For Area of smaller common area = 2b from below figure

Area b = Area of circular arc(2b+a) – Area of triangle (a+b)

= $\frac{1}{4}\left(36\pi\ \right)-\ \frac{1}{2}\left(6\times\ 6\right)$  =$9\pi\ -18$

Area of common part of smaller circle = 2b = $18\pi\ -36$

Therefore required area = $576-144\pi+\left(4\times\ 36\pi\right)-8\times\ \left(18\pi\ -36\right)$

= $288+144\pi\ $

None of the above are correct

10) Answer (B)

AC= $\sqrt{\ AB^2\ +BC^2}=\ \sqrt{\ 6^2+8^2\ }=10$

In-radius of right angled triangle = $\frac{\left(a+b-h\right)}{2}$

Inradius = $\frac{\left(6+8-10\right)}{2}=2$

11) Answer (A)

Midpoint of P(x1,y1) , Q(x2,y2) = C($\frac{x1+x2}{2},\ \frac{y1+y2}{2}$)

So $y=\frac{4-2}{2},\ -1=\ \frac{x+4}{2}$

On solving x=-6 and y=1

12) Answer (B)

Since AB is the diameter $\angle\ ADB\ =\ 90^0$

Which gives $\angle\ DAB\ =\ 50^0$

ABCD is cyclic quadrilateral so $\angle\ A+\angle\ C\ =\ 180^0$

Thus $\angle\ DCB\ =\ 130^0$

In$\bigtriangleup\ $ BCD, 2x+130 = 150

$x\ =\ 25^0$

13) Answer (C)

We have MN || AB
Now let area of CMN be A
so area of ABMN will be 2A
Now Area of triangle ABC will be 3A

Now since MN || AB
so we can say CMN is similar to CAB
So we can say
(CM/CA)^2 = Area of CMN : Area of CAB
so we can say CM :CA =$1:\sqrt{\ 3}$
Now therefore CM :AM = $1:\sqrt{\ 3}-1\ =\ \sqrt{\ 3}+1:2$

14) Answer (A)

$\angle\ DCB\ =90^0$ (Since each angle in a square is 90)

$\angle\ BCE\ =60^0$ (Since each angle in an equilateral triangle is 60)

$\angle\ DCE\ =90^0+ 60^0$  = $150^0$

In $\triangle\ DCE$, the sides DC and CE are equal, so the angles opposite to them are equal.

$\angle\ DCE$ = $\angle\ CDE$ = $\ \frac{\ 180-150}{2}$

=$15^0$

A is the correct answer.

15) Answer (B)

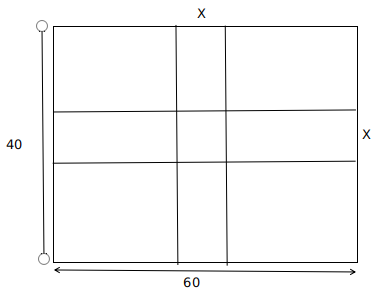
Area of the park = (60 x 40) m² = 2400 m².

Area of the lawn = 2109 m².

Area of the crossroads = (2400 – 2109) m² = 291 m².

Let the width of the road be x metres.

Then, 60x + 40x – x² = 291

x² – 100x + 291 = 0

(x – 97)(x – 3) = 0

x = 3.

B is the correct answer

16) Answer (D)

Let the radius of solid sphere be r.

The volume of sphere $V_s$= $\ \frac{\ 4}{3}$ πr³

It is melted and recast into a right circular cone of radius r and height h.

The volume of cone $V_c$= $\ \frac{\ 1}{3}$ πr²h

The same volume of material is used for recasting. Therefore,

$V_s=V_c$

$\ \frac{\ 4}{3}$πr³ =  $\ \frac{\ 1}{3}$ πr²h

h = 4r

$\ \frac{\ h}{r}$  = 4
D is the correct answer.

17) Answer (C)

Area of the tunnel to be filled with concrete = 16*8-$\pi\ \left(32\right)$

Length of the length along which the tunnel has to be filled with concrete = 500m

Volume = 16*8-$\pi\ \left(32\right)$*500

= $32(4-\pi)$*500

Cost of concrete per $1 m^3$ = 1000

Cost of $32(4-\pi)$*500 = $32(4-\pi)$*500*1000

=$16(4-\pi)*10^{6}$

C is the correct answer.

18) Answer (C)

Join BD

Area of ABCD = area of ABD + area of BCD

In ABD $AB^2\ +\ AD^2\ =BD^2$

Therefore   $24^{2\ }+\ 18^{2\ }=\ BD^2$ , on solving BD= 30

also $30^{2\ }+\ 40^2\ =50^2$ which implies BCD is also a right-angled triangle

Area of ABD = $\frac{1}{2}\times\ 24\times\ 18$ = 216

Area of BCD = $\frac{1}{2}\times\ 30\times\ 40$= 600

Area of ABCD = 816

19) Answer (A)

$y^2 = 4x$  , a =1

Equation of normal is $y=mx-2am-am^3$

=> $y=mx-2m-m^3$

It passes through R(9,-6)

=> -6 = 9m -2m – $m^3$

=> $\left(m+1\right)\left(m-3\right)\left(m+2\right)=0$

=> m =-1,3,-2

$y^2 = 4x$

$2yy’=4\ =>\ y’=\frac{2}{y}$

Slope of the normal = -y/2

-y/2 = -1 => y=2 => x= 1  hence one point is P(1,2)

-y/2 = 3 => y=-6 => x=9 hence secoond point is R(9,-6)

-y/2=-2 => y =4 => x=4 hence third point is Q(4,4)

PQ = $\sqrt{\ 13}$

20) Answer (B)

$x^2 — 7x + 6 = 0$ => x= 1, x=6$PM\ =\sqrt{\ PW^2-MW^2}$

$y^2 — 14y + 40 = 0$ => y= 4, y=10

$W\ =\ \left(\frac{1+6}{2},\frac{4+10}{2}\right)\ =\ \left(\frac{7}{2},7\right)$

QR = 6-1 =5

r = (10-4)/2 = 3

PW = r= 3

MW = QR/2 = 5/2

$PM\ =\sqrt{\ PW^2-MW^2}$ = $\frac{\sqrt{\ 11}}{2}$

PQ=2PM = $\sqrt{\ 11}$

Area of PQRS = QR x PQ = $5\sqrt{\ 11}$

Get 5 TISSNET mocks at just Rs.299

Download TISSNET Previous Papers PDF