Geometry Questions for NMAT:

Download Geometry Questions for NMAT PDF. Top 10 very important Geometry Questions for NMAT based on asked questions in previous exam papers.

Download Geometry Questions for NMAT

Get 5 NMAT Mocks for Rs. 499

Take NMAT mock test

Question 1: From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is

a) $\frac{\sqrt{3}s^{2}}{2}$

b) $\frac{2s^{2}}{\sqrt{3}}$

c) $\frac{s^{2}}{2\sqrt{3}}$

d) $\frac{s^{2}}{\sqrt{3}}$

Question 2: Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6cm and is a tangent to C2, then the diameter, in cm, of C1 is

Question 3: The sum of the perimeters of an equilateral triangle and a rectangle is 90cm. The area, T, of the triangle and the area, R, of the rectangle, both in sq cm, satisfying the relationship $R=T^{2}$. If the sides of the rectangle are in the ratio 1:3, then the length, in cm, of the longer side of the rectangle, is

a) 27

b) 21

c) 24

d) 18

Question 4: Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to

a) 8.8

b) 7.8

c) 6.6

d) 7.2

Question 5: The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is

a) $\frac{14\pi}{3}$

b) $\frac{123\pi}{7}$

c) $\frac{12\pi}{5}$

d) $\frac{205\pi}{9}$

Question 6: In a trapezium $ABCD$, $AB$ is parallel to $DC$, $BC$ is perpendicular to $DC$ and $\angle BAD=45^{0}$. If $DC$ = 5cm, $BC$ = 4 cm,the area of the trapezium in sq cm is

Question 7: The points (2,1) and (-3,-4) are opposite vertices of a parallelogram.If the other two vertices lie on the line $x+9y+c=0$, then c is

a) 12

b) 13

c) 15

d) 14

Question 8: A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is

a) $\frac{6\pi}{25}$

b) $\frac{5\pi}{18}$

c) $\frac{3\pi}{25}$

d) $\frac{2\pi}{15}$

Question 9: On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is

a) $3\sqrt{\pi}(5+\frac{12}{\pi})$

b) $4\sqrt{\pi}(3+\frac{9}{\pi})$

c) $3\sqrt{\pi}(\frac{5}{2}+\frac{6}{\pi})$

d) $5\sqrt{\pi}(3+\frac{9}{\pi})$

Question 10: A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is

a) 243

b) 232

c) 256

d) 264

Join 7K MBA Aspirants Telegram Group

Download Highly Rated CAT preparation App

Answers & Solutions:

1) Answer (D)

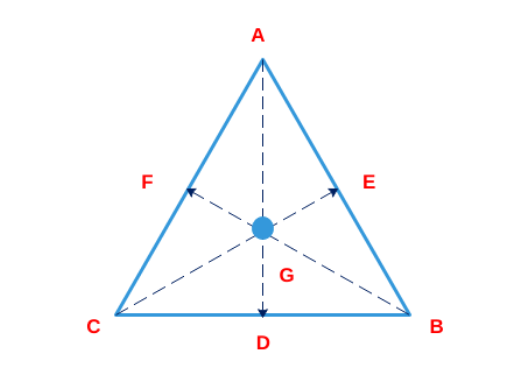
Based on the question: AD, CE and BF are the three altitudes of the triangle. It has been stated that {GD+GE+GF = s}

Now since the triangle is equilateral, let the length of each side be “a”. So area of triangle will be

$\frac{1}{2}\times\ GD\times\ a+\ \frac{1}{2}\times\ GE\times\ a\ +\frac{1}{2}\times\ GF\times\ a=\frac{\sqrt{\ 3}}{4}a^2$

Now $GD+GE+GF=\frac{\sqrt{\ 3}a}{2}$ or $s=\frac{\sqrt{\ 3}a}{2}\ or\ a=\frac{2s}{\sqrt{\ 3}}$

Given the area of the equilateral triangle = $\ \frac{\sqrt{3}}{4}a^2\ $ ; substituting the value of ‘a’ from above, we get the area {in terms ‘s’}= $\frac{s^2}{\sqrt{3}}$

2) Answer: 10

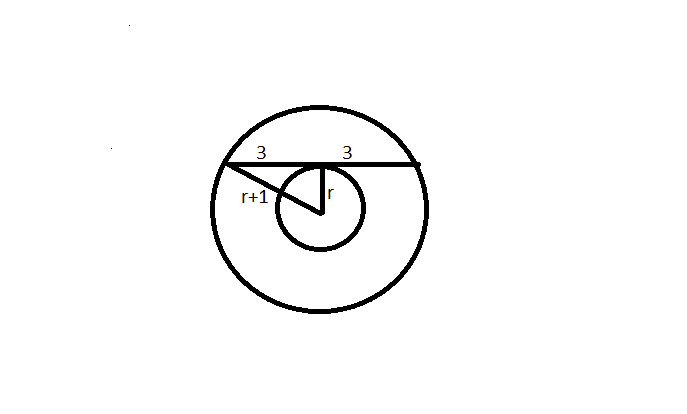
Now we know that the perpendicular from the centre to a chord bisects the chord. Hence at the point of intersection of tangent, the chord will be divided into two parts of 3 cm each. As you can clearly see in the diagram, a right angled triangle is formed there.

Hence   $\left(r+1\right)^2=r^2+9$ or $r^{2\ }+1+2r\ =\ r^2+9\ or\ 2r=8\ or\ r=4cm$

Hence the radius of the larger circle is 5cm and diameter is 10cm.

3) Answer (A)

Let the sides of the rectangle be “a” and “3a” m. Hence the perimeter of the rectangle is 8a.

Let the side of the equilateral triangle be “m” cm. Hence the perimeter of the equilateral triangle is “3m” cm. Now we know that 8a+3m=90……(1)

Moreover area of the equilateral triangle is $\frac{\sqrt{\ 3}}{4}m^2$ and area of the rectangle is $3a^2$

According to the relation given $\left(\frac{\sqrt{\ 3}}{4}m^2\right)^{^2}=\ 3a^2$

$\frac{3}{16}m^4=\ 3a^2\ or\ a^2=\frac{m^4}{16}$

$a=\frac{m^2}{4}$

Substituting this in (1) we get $2m^2+3m-90\ =0$ solving this we get m=6 (ignoring the negative value since side can’t be negative)

Hence a=9 and the longer side of the rectangle will be 3a=27cm

4) Answer (A)

We can form the following figure based on the given information:

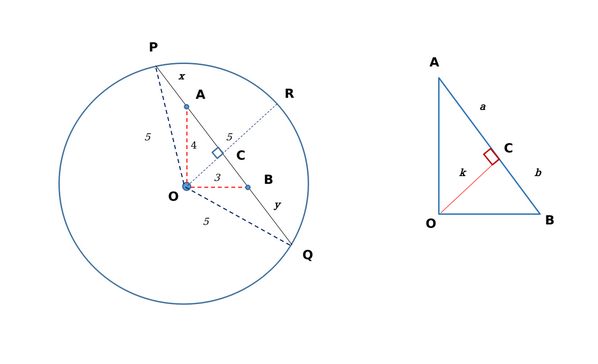
Since OA = 4 m and OB=3 m; AB = 5 m. OR bisects the chord into PC and QC.

Since AB = 5 m, we have $a+b = 5      …(i)$  Also, $4^2\ -k^2=a^2…\left(ii\right)$ and $3^2\ -k^2=b^2…\left(iii\right)$

Subtracting (iii) from (ii), we get: $a^2\ -b^2=7…\left(iv\right)$

Substituting (i) in (iv), we get $a – b = 1.4      …(v)$; $\left[\left(a+b\right)\left(a\ -b\right)=7;\ \therefore\ \left(a-b\right)=\frac{7}{5}\right]$

Solving (i) and (v), we obtain the value of $a=3.2$ and $b=1.8$

Hence, $k^2\ =\ 5.76$

Moving on to the larger triangle $\triangle\ POC$, we have $5^2-k^2=\left(x+a\right)^2$;

Substituting the previous values, we get: $(25-5.76)=\left(x+3.2\right)^2$

$\sqrt{19.24}=\left(x+3.2\right)$ or $x = 1.19 m$

Similarly, solving for y using $\triangle\ QOC$, we get $y=2.59 m$

Therefore, $PQ = 5+2.59+1.19 = 8.78 \approx\ 8.8 m$

Hence, Option A is the correct answer.

5) Answer (D)

Equation of circle $x^2+y^2+2gx+2fy+c=0$

It passes through (0,0), (4,0) and (3,9). Substitute each point in the above equation:

=> On substituting the value (0,0) in the above equation, we obtain: $c=0$

=> On substituting the value (4,0) in the above equation, we obtain:  $16+0+8g+0 = 0$ ; $g=-2$

=> On substituting the value (3,9) in the above equation, we obtain: $9+81-12+18f = 0$ ; $f= -13/3$

Radius of the circle r = $\sqrt{\ g^2+f^2-c}$ => $r^2=\frac{205}{9}$

Therefore, Area = $\pi\ r^2=\frac{205\pi\ }{9}$

6) Answer: 28

Given, BC = DE = 4

CD = BE = 5

In triangle ADE, EAD=45^{0}$

$\tan\ 45\ =\ \frac{DE}{AE}$ => AE = 4

Area of trapezium = Area of rectangle BCDE + Area of triangle AED

= 20 + 8 = 28

7) Answer (D)

The midpoints of two diagonals of a parallelogram are the same

Hence the midpoint of (2,1) and (-3,-4) lie on $x+9y+c=0$

midpoint of (2,1) and (-3,-4) = ($\frac{2-3}{2},\frac{1-4}{2}$) = (-1/2 , -3/2)

Keeping this cordinates in the above line equation, we get c = 14

8) Answer (A)

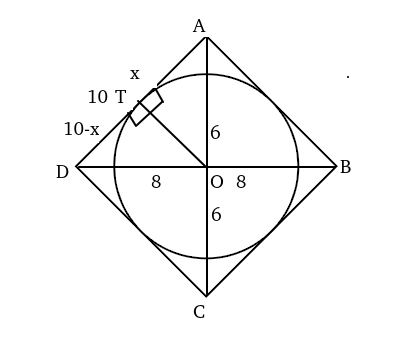
Let the length of radius be ‘r’.

From the above diagram,

$x^2+r^2=6^2\ $….(i)

$\left(10-x\right)^2+r^2=8^2\ $—-(ii)

Subtracting (i) from (ii), we get:

x=3.6 => $r^2=36-\left(3.6\right)^2$ ==> $r^2=36-\left(3.6\right)^2\ =23.04$.

Area of circle = $\pi\ r^2=23.04\pi\ $

Area of rhombus= 1/2*d1*d2=1/2*12*16=96.

.’. Ratio of areas = 23.04$\pi\ $/96=$\frac{6\pi}{25}$

9) Answer (A)

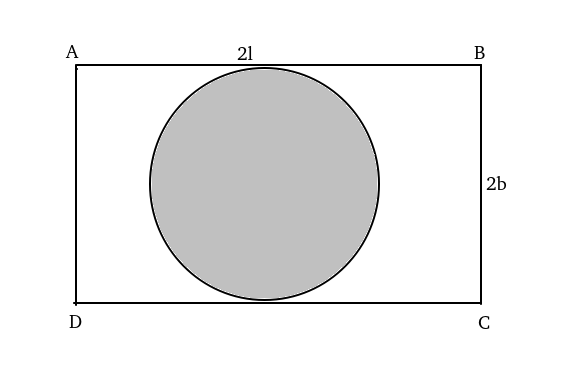
Let ABCD be the rectangle with length 2l and breadth 2b respectively.

Area of the circle i.e. area of painted region = $\pi\ b^2$.

Given, 4lb-$\pi\ b^2$=(2/3)$\pi\ b^2$.

=> 4lb=(5/3)$\pi\ b^2$.

=>l=$\frac{5\pi}{12}b$.

Given, 4lb=135 => 4*$\frac{5\pi}{12}b^2$=135 => b= $\frac{9}{\sqrt{\ \pi\ }}$

=> l=$\frac{15}{4}\sqrt{\ \pi\ }$
Perimeter of rectangle =4(l+b)=4($\frac{15}{4}\sqrt{\ \pi\ }$+$\frac{9}{\sqrt{\ \pi\ }}$ )=$3\sqrt{\pi}(5+\frac{12}{\pi})$.

Hence option A is correct.

10) Answer (A)

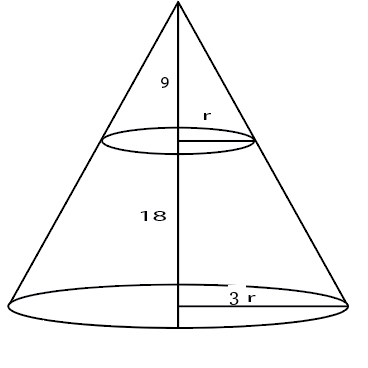
Let the base radius be 3r.

Height of upper cone is 9 so, by symmetry radius of upper cone will be r.

Volume of frustum=$\frac{\pi}{3}\left(9r^2\cdot27-r^2.9\right)$

Volume of upper cone = $\frac{\pi}{3}.r^2.9$

Difference= $\frac{\pi}{3}\cdot9\cdot r^2\cdot25=225$ => $\frac{\pi}{3}\cdot r^2=1$

Volume of larger cone = $\frac{\pi}{3}\cdot9r^2\cdot27=243$

Get 5 NMAT Mocks for Rs. 499

We hope this Geometry Questions for NMAT pdf for NMAT exam will be highly useful for your Preparation.