Geometry Questions for CMAT 2022 – Download PDF

Download CMAT 2022 Geometry Questions pdf by Cracku. Very Important Geometry Questions for CMAT 2022 based on asked questions in previous exam papers. These questions will help your CMAT preparation. So kindly download the PDF for reference and do more practice.

Download Geometry Questions for CMAT

Get 5 CMAT mocks at just Rs.299

Download CMAT previous papers PDF

Question 1: Let ABCD be a parallelogram. The lengths of the side AD and the diogonal AC are 10cm and 20cm, respectively. If the angle $\angle ADC$ is equal to $30^{0}$ then the area of the parallelogram, in sq.cm is

a) $\frac{25(\sqrt{5}+\sqrt{15})}{2}$

b) $25(\sqrt{3}+\sqrt{15})$

c) $\frac{25(\sqrt{3}+\sqrt{15})}{2}$

d) ${25(\sqrt{5}+\sqrt{15})}$

Question 2: If a triangle ABC, $\angle BCA=50^{0}$. D and E are points on $AB$ and $AC$, respectively, such that $AD=DE$. If F is a point on $BC$ such that $BD=DF$, then $\angle FDE$, in degrees, is equal to

a) 72

b) 80

c) 100

d) 96

Question 3: A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is

Question 4: The cost of fencing a rectangular plot is ₹ 200 per ft along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is

a) 120000

b) 90000

c) 100000

d) 160000

Question 5: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is

a) 30

b) 40

c) 25

d) 20

Download CMAT Previous Papers PDF

Take CMAT Mock Tests

Question 6: A circle of diameter 8 inches is inscribed in a triangle ABC where $\angle ABC = 90^\circ$. If BC = 10 inches then the area of the triangle in square inches is

Question 7: Suppose the length of each side of a regular hexagon ABCDEF is 2 cm.It T is the mid point of CD,then the length of AT, in cm, is

a) $\sqrt{13}$

b) $\sqrt{14}$

c) $\sqrt{12}$

d) $\sqrt{15}$

Question 8: If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length, in cm, of each side of the hexagon is

a) $4\sqrt{6}$

b) $6\sqrt{6}$

c) $\sqrt{6}$

d) $2\sqrt{6}$

Question 9: The topmost point of a perfectly vertical pole is marked A. The pole stands on a flat ground at point D. The points B and C are somewhere between A and D on the pole. From a point E, located on the ground at a certain distance from D, the points A, B and C are at angles of 60, 45 and 30 degrees respectively. What is AB : BC : CD?

a) $(3 + \sqrt 3) : (1 + \sqrt 3) : 1$

b) $(3 – \sqrt 3) : 1 : (\sqrt 3 – 1)$

c) 1 : 1 : 1

d) $(3 – \sqrt 3) : (\sqrt 3 – 1) : 1$

e) $(\sqrt 3 – 1) : 1 : (3 – \sqrt 3)$

Question 10: The six faces of a wooden cube of side 6 cm are labelled A, B, C, D, E and F respectively. Three of these faces A, B, and C are each adjacent to the other two, and are painted red. The other three faces are not painted. Then, the wooden cube is neatly cut into 216 little cubes of equal size. How many of the little cubes have no sides painted?

a) 125

b) 135

c) 91

d) 108

e) 100

Question 11: Rajesh, a courier delivery agent, starts at point A and makes a delivery each at points B, C and D, in that order. He travels in a straight line between any two consecutive points. The following are known: (i) AB and CD intersect at a right angle at E, and (ii) BC, CE and ED are respectively 1.3 km, 0.5 km and 2.5 km long. If AD is parallel to BC, then what is the total distance (in km) that Rajesh covers in travelling from A to D?

a) 10.2

b) 12

c) 11.5

d) 5.5

e) 18

Question 12: Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6cm and is a tangent to C2, then the diameter, in cm, of C1 is

Question 13: The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is

a) $\frac{14\pi}{3}$

b) $\frac{123\pi}{7}$

c) $\frac{12\pi}{5}$

d) $\frac{205\pi}{9}$

Question 14: A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is

a) 243

b) 232

c) 256

d) 264

Question 15: The area bounded by the curve $y^2 = x^2 – x^4$ is

a) $\frac{4}{3}$

b) $\frac{2}{3}$

c) $\frac{3}{4}$

d) $\frac{3}{2}$

Take CMAT Mock Tests

Question 16: The locus of the centre of a circle that passes through the origin and cuts off a length 2a from the line y = c is

a) $x^2 + 2cx = a^2 + c^2$

b) $x^2 + 2cy = a^2 + c^2$

c) $y^2 + 2cx = a^2 + c^2$

d) $y^2 + 2cy = a^2 + c^2$

Question 17: A curve is drawn such that the slope at any point P = (x,y) is equal to x. The curve represents a family of

a) Circles

b) Parabolas

c) Ellipses

d) Hyperbolas

Question 18: The radius of the incircle of the triangle formed by the x-axisand the lines 3x + 4y – 24 = 0, 3x – 4y + 24 = 0 is

a) $\frac{7}{3}$

b) $\frac{8}{3}$

c) $2$

d) $3$

Question 19: Meera and Sameera start moving from the same point. Meera goes 4 kms west followed by 3 kms north. Sammera goes 4 kms east and then a right turn and keeps going for 3 kms. What is the shortest distance between the two of them?

a) 10 kms

b) 12 kms

c) 8 kms

d) 14 kms

Question 20: The intersection of two cubes cannot be

a) cube

b) triangle

c) rectangle

d) none of these

Enroll to CAT 2022 Complete Course

Answers & Solutions:

1) Answer (B)

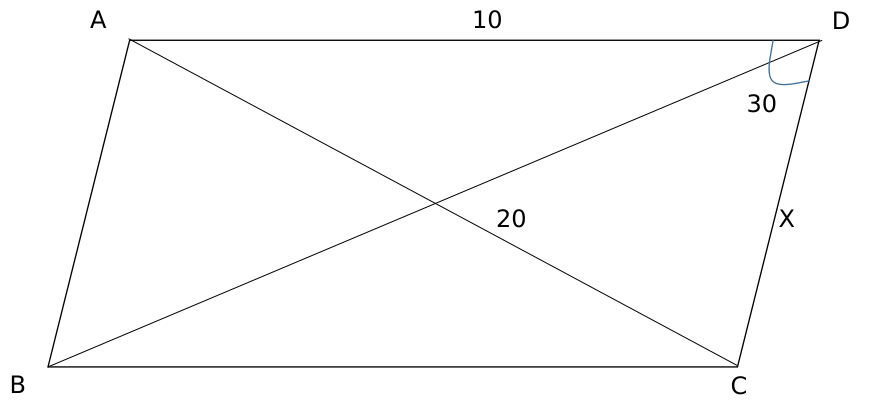
Applying cosine rule in triangle ACD,

$100+X^2-2\times\ 10\times\ X\cos30=400$

$X^2-10X\sqrt{\ 3}-300=0$

Solving, we get X = $\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)$

Hence, area = 10Xsin 30 = $\frac{\left(\frac{10\sqrt{\ 3}+10\sqrt{\ 15}}{2}\right)10}{2}$

= $25(\sqrt{3}+\sqrt{15})$

2) Answer (B)

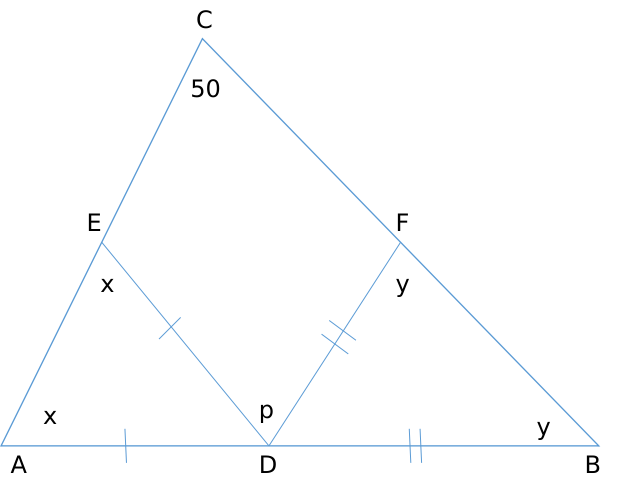
We need to find out p.

Angle ADE = 180 – 2x

Angle BDF = 180 – 2y

Now, 180 – 2y + p + 180 – 2x = 180 [Straight line = 180 deg]

p = 2x + 2y – 180

Also, x + y + 50 = 180 [Sum of the angles of triangle = 180]

x + y = 130

p = 260 – 180 = 80 degrees.

3) Answer: 3500

We can say 40m is the perimeter of the park
so side of rhombus = 10
Now $\frac{1}{2}\times\ d_1\times\ d_2\ =\ 96$
so we get $\ d_1\times\ d_2\ =\ 192$   (1)
And as we know diagonals of a rhombus are perpendicular bisectors of each other :
so $\ \frac{d_1^2}{4}+\ \frac{d_2^2}{4}=\ 100$
so we get $\ d_1^2+\ d_2^2=\ 400$    (2)
Solving (1) and (2)
We get $d_1=12$ and$d_2=16$
Now the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is= (12+16)(125) =3500

4) Answer (A)

Let us draw the rectangle.

Now, definitely, three sides should be fenced at Rs 100/ft, and one side should be fenced at Rs 200/ft.

In this question, we are going to assume that the L is greater than B.

Hence, the one side painted at Rs 200/ft should be B to minimise costs.

Hence, the total cost = 200B + 100B + 100L + 100L = 300B + 200L

Now, L x B = 60000

B = 60000/L

Hence, total cost = 300B + 200L = 18000000/L + 200L

To minimise this cost, we can use AM>=GM,

$\frac{\frac{18000000}{L}+200L}{2}\ge\sqrt{\ \frac{18000000}{L}\times\ 200L}$

$\frac{18000000}{L}+200L\ge2\sqrt{\ 18000000\times\ 200}$

$\frac{18000000}{L}+200L\ge2\times\ 60000$

Hence, minimum cost = Rs 120000.

5) Answer (A)

We are given that :

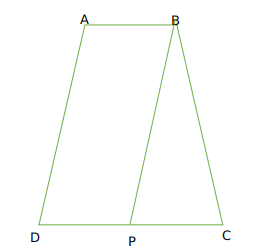
Let DP =x
So AB =x
Now DP=CP
So CD = 2x
Now let height of trapezium be h
we can say A(Parallelogram ABPD ) = xh
And A (BPC) =$\frac{1}{2}xh$
Now by condition$xh-\frac{1}{2}xh=10$
$\frac{xh}{2}=10$
so xh =20
Now therefore area of trapezium ABCD = $\frac{1}{2}\left(x+2x\right)h\ =\ \frac{3}{2}xh\ =\ 30$

6) Answer: 120

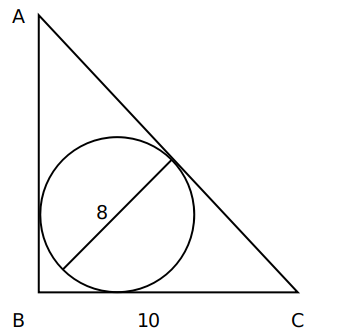
We know that Inradius=$\frac{\left(Perpendicular+Base-Hypotenuse\right)}{2}$

$4=\frac{\left(p+10-h\right)}{2}$

h-p = 2 or h= p+2.

Now, $p^2+100\ =\ h^2$

$p^2+100\ =\ \left(p+2\right)^2$

$p^2+100\ =\ p^2+4p+4$

4p = 96

p=24.

Hence, Area = $\frac{1}{2}\times\ 10\times\ 24\ =\ 120$.

7) Answer (A)

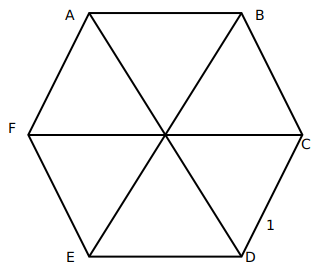
Since a regular hexagon can be considered to be made up of 6 equilateral triangles, a line joining the farthest vertices of a hexagon can be considered to be made up using the sides of two opposite equilateral triangle forming the hexagon. Hence, its length should be twice the side of the hexagon, in this case, 4 cm.

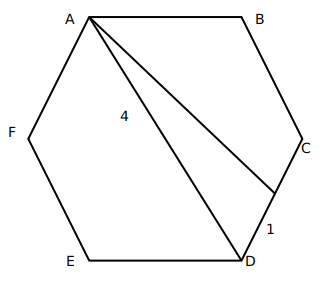
Now, AD divided the hexagon into two symmetrical halves. Hence, AD bisects angle D, and hence, angle ADC is $60^{\circ\ }$.

We can find out the value of AT using cosine formula:

$AT^2=\ 4^2+1^2-2\times\ 1\times\ 4\cos60$

$AT^2=\ 17-4=13$

$AT=\sqrt{\ 13}$

8) Answer (D)

Area of a regular hexagon = $\frac{3\sqrt{3}}{2}x^2$

Area of an equilateral triangle = $\frac{\sqrt{3}}{4}\left(a\right)^2$ ; where a = side of the triangle

Since the area of the two figures are equal, we can equate them as folllows: $\frac{3\sqrt{3}}{2}x^2=\frac{\sqrt{3}}{4}\left(12\right)^2$

On simplifying: $x^2=24\ $

$\therefore\ x=2\sqrt{6}$

9) Answer (D)

Let ED = $\sqrt{\ 3}x$
In triangle CDE, $\tan\ 30\ =\ \frac{CD}{\sqrt{\ 3}x}$ => CD = x

In triangle BDE, $\tan\ 45\ =\ \frac{BD}{\sqrt{\ 3}x}$ => BD = $\sqrt{\ 3}x$ => BC = $\sqrt{\ 3}x\ -x$

In triangle ADE, $\tan\ 60\ =\ \frac{AD}{\sqrt{\ 3}x}$ => AD = 3x => AB = $3x\ -\ \sqrt{\ 3}x$

AB : BC : CD = $(3 – \sqrt 3) : (\sqrt 3 – 1) : 1$

10) Answer (A)

Since A, B and C are adjacent faces. If we remove them, the resultant solid will also be a cube with side 5.

Hence total number of cubes unpainted = $5^3$ = 125

11) Answer (C)

Given, CE=0.5, BC = 1.3 and ED=2.5

Triangle CEB is a right-angled triangle => EB = 1.2

Triangles ECB is similar to triangle EDA

EB/EC = AE/ED  => AE = 6

Hence total distance travelled = AB + BC + CD = 7.2 + 1.3 + 3.5 = 11.5km

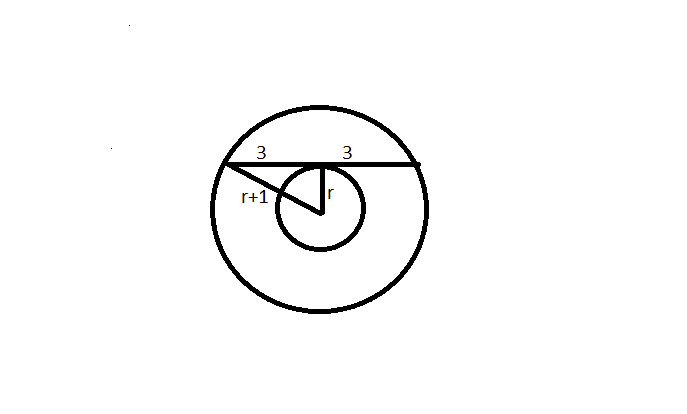
12) Answer: 10

Now we know that the perpendicular from the centre to a chord bisects the chord. Hence at the point of intersection of tangent, the chord will be divided into two parts of 3 cm each. As you can clearly see in the diagram, a right angled triangle is formed there.

Hence   $\left(r+1\right)^2=r^2+9$ or $r^{2\ }+1+2r\ =\ r^2+9\ or\ 2r=8\ or\ r=4cm$

Hence the radius of the larger circle is 5cm and diameter is 10cm.

13) Answer (D)

Equation of circle $x^2+y^2+2gx+2fy+c=0$

It passes through (0,0), (4,0) and (3,9). Substitute each point in the above equation:

=> On substituting the value (0,0) in the above equation, we obtain: $c=0$

=> On substituting the value (4,0) in the above equation, we obtain:  $16+0+8g+0 = 0$ ; $g=-2$

=> On substituting the value (3,9) in the above equation, we obtain: $9+81-12+18f = 0$ ; $f= -13/3$

Radius of the circle r = $\sqrt{\ g^2+f^2-c}$ => $r^2=\frac{205}{9}$

Therefore, Area = $\pi\ r^2=\frac{205\pi\ }{9}$

14) Answer (A)

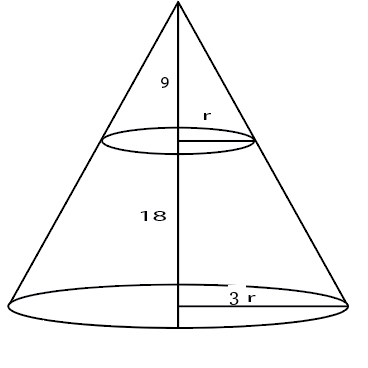
Let the base radius be 3r.

Height of upper cone is 9 so, by symmetry radius of upper cone will be r.

Volume of frustum=$\frac{\pi}{3}\left(9r^2\cdot27-r^2.9\right)$

Volume of upper cone = $\frac{\pi}{3}.r^2.9$

Difference= $\frac{\pi}{3}\cdot9\cdot r^2\cdot25=225$ => $\frac{\pi}{3}\cdot r^2=1$

Volume of larger cone = $\frac{\pi}{3}\cdot9r^2\cdot27=243$

15) Answer (A)

Since we see that both y and x has even terms, it implies the curve is symmetric along x-axis as well as y-axis.

Required area = 4*(area in quadrant I)

Area in quadrant I is given by

A =$_0\int^1\sqrt{\ x^2-x^4}dx\ $

A = $_0\int^1x\sqrt{1-x^2}dx$

take $1-x^2\ =\ t^2$, then $-2x\ dx\ =\ 2\ t\ dt$. when x =0 then t = 1 and  when x = 1 then t = 0

Updated integral can be written as

$\int_0^1t^{2\ }dt$ = $\left[\frac{t^3\ }{3}\right]_0^1\ =\ \ \frac{\ 1}{3}$

Required area = 4*A = $\ \frac{\ 4}{3}$

16) Answer (B)

Let the locus of the center be represented by (h,k)

Since it passes through origin. Radius r = $\sqrt{\ h^2+k^2}$

Since it cuts off chord of length = 2a on y=c. We draw 1 perpendicular bisector of the chord till the center and make a line which is intersecting point of line y=c and the circle.

We obtain a right triangle that has “r” as its hypotenuse and a and |c-k| as its sides.

Applying Pythogoras theorm,

$r^2\ =\ a^2\ +\ \left(c-k\ \right)^2$

it implies

$h^2+k^2\ =\ a^2\ +\ \left(c-k\ \right)^2$

$h^2+k^2\ =\ a^2\ +\ c^2+k^2\ -2ck$

$h^2+2ck\ =\ a^2\ +\ c^2$

replacing (h,k) by (x,y)

we get $x^2+2cy\ =\ a^2\ +\ c^2$

17) Answer (B)

It is given that the slope of the curve at any point P is equal to x.

It is also known that, to find the slope at any point P(x,y), we can find $\ \frac{\ dy}{dx}$ of the curve at that point P.

For $\ \frac{\ dy}{dx}$ of a curve to be equal to x, the original curve must be of the form $\ ax^2\ +c$, where a and c are any constants.

Now, y= $\ ax^2\ +c$ represents a family of parabolas.

Hence, option B

18) Answer (B)

For 3x+4y-24=0 can be re-written as $3x+4y=24$

=>$\frac{3x+4y\ \ }{24}=1$

=>$\ \frac{\ x}{8}+\ \frac{\ y}{6}=1$.

So, this becomes the equation of the straight line of the form $\ \frac{\ x}{a}+\ \frac{\ y}{b}=1$, where a and b are x and y intercepts respectively. The X and Y intercepts for this equation are 8 and 6 respectively.

Similarly 3x-4y+24=0 can be re-written as $\ \frac{\ x}{-8}+\ \frac{\ y}{6}=1$. The X and Y intercepts for this equation are 8 and -6 respectively.

So, we get the following triangle and the incircle can be drawn as:

So, the triangle has sides of length 10,10 and 16.

Area of the triangle= $\ \frac{\ 1}{2}\times\ Base\times\ Height$= $\ \frac{\ 1}{2}\times\ 16\times\ 6$= 48

We know that r*s= Area of the triangle, where r is the inradius and s is the semi-perimeter. s= $\ \frac{\ 1}{2}\left(16+10+10\right)$= 18

So, 18r= 48

=> Or, r= $\ \frac{\ 48}{18}=\ \ \frac{\ 8}{3}$

19) Answer (A)

Using pythagoras theorem, we can clearly see from above that the shortest distance between Sameera and Meera is 10km.

20) Answer (A)

Cubes are a 3-D figure, and so, the intersection of two 3-D figure must be a 2-D figure.

So, Cube cannot be the intersection of two cubes.

Enroll to CAT 2022 Complete Course

Download CMAT Previous Papers PDF