Geometry Circles Questions for MAH-CET

Here you can download a free Geometry Circles questions PDF with answers for MAH MBA CET 2022 by Cracku. These are some tricky questions in the MAH MBA CET 2022 exam that you need to find the answers to the given Geometry Circles questions. These questions will help you to practice and solve the Geometry Circles questions in the MAH MBA CET exam. Utilize this PDF practice set, which is one of the best sources for practising and includes detailed answers. Click on the below link to download the Geometry Circles MCQ PDF for MAH MBA CET 2022 for free.

Download Geometry Circles Questions for MAH-CET

Enroll to MAH-CET 2022 Crash Course

Question 1: The figure below shows two concentric circles with centre 0. PQRS is a square, inscribed in the outer circle. It also circumscribes the inner circle, touching it at points B, C, D and A. What is the ratio of the perimeter of the outer circle to that of polygon ABCD?

a) $\frac{\pi}{4}$

b) $\frac{3\pi}{2}$

c) $\frac{\pi}{2}$

d) $\pi$

1) Answer (C)

View Video Solution

Solution:

By symmetry, it is safe to assume that the polygon ABCD is a square. So, AB = PO. The perimeter of the inner square = 4 AB. The perimeter of the outer circle = $ 2 \pi \times AB$

So, ratio = $ \frac{2 \pi \times AB}{4AB}$ = $ \frac{\pi}{2}$

Question 2: Three circles, each of radius 20, have centres at P, Q and R. Further, AB = 5, CD = 10 and EF = 12. What is the perimeter of ΔPQR ?

a) 120

b) 66

c) 93

d) 87

2) Answer (C)

View Video Solution

Solution:

As radius of circle is 20, lengths of PR, QR and PQ will be (15+5+15) , (10+10+10) , (8+12+8) respectively.
So perimeter will be = 28 + 30 + 35 = 93

Question 3: The sum of the areas of two circles, which touch each other externally, is $153\pi$. If the sum of their radii is 15, find the ratio of the larger to the smaller radius.

a) 4

b) 2

c) 3

d) None of these

3) Answer (A)

View Video Solution

Solution:

Given:
$\pi((r_1)^2 + (r_2)^2) = 153\pi$
So
$(r_1)^2 + (r_2)^2 = 153$
Or $((r_1) + (r_2))^2 – 2(r_1)(r_2) = 153$
Or  $(r_1)(r_2) = 36$ and $(r_1) + (r_2) = 15$
$r_1 = 12$
$r_2 = 3$
Ratio = 4

Question 4: From a circular sheet of paper with a radius 20 cm, four circles of radius 5 cm each are cut out. What is the ratio of the uncut to the cut portion?

a) 1 : 3

b) 4 : 1

c) 3 : 1

d) 4 : 3

4) Answer (C)

View Video Solution

Solution:

Area of the large sheet =$\pi {20}^2$

Area of the 4 circle of sheet = $4\pi {5}^2$

Required ratio =[$\pi {20}^2 – 4\pi {5}^2$]:[$4\pi {5}^2$] = 4-1 = 3:1

Question 5: In a figure, $\triangle ABC$ is a right angled triangle at $C$, semicircles are drawn on $AC$, $BC$ and $AB$’s diameter. Find the area of the shaded region.

Note: Figure not as per scale

a) 336

b) 676

c) 196

d) 556

5) Answer (A)

Solution:

Area of shaded region = area of semicircle on BC + area of semicircle of AC – area of unshaded semicircle regions
Area of unshaded semicircle regions = area of semicircle on AB – area of triangle ABC
Given,
AB = 50, BC = 14
In triangle ABC, $AC^2+BC^2 = AB^2$
Solving we get,
AC = 48
Area of unshaded semicircle regions = $\pi\ \left(25\right)^2\ $ – $\frac{1}{2}\times\ 48\times\ 14$ = $625\pi\ -336$
Area of shaded region = $576\pi\ +49\pi\ -625\pi\ +336$ = 336

The answer is option A.

Take Free MAH-CET mock tests here

Enrol to 5 MAH CET Latest Mocks For Just Rs. 299

Question 6: Three small identical circles are inscribed inside an equilateral triangle with length $10\sqrt{3}$ cm as shown in the figure. The radius of each small circle is 2 cm A big circle touches these three circles as shown in the figure. Find the ratio of the area of the big circle with that of the area of the small circle. (figure not as per scale)

a) 4:1

b) 2:1

c) 3:1

d) 5:1

6) Answer (A)

Solution:

Height of triangle = $\left(10\sqrt{3}\right)\times\ \left(\frac{\sqrt{3}}{2}\right)=15$

Distance between the centroid of the triangle and the vertex= $15\times\ \frac{2}{3}=10$

Since in-radius is one-third of the height of the triangle

therefore, length of the line from vertex to the point where small circle and big circle touch each other = $2\times3=6$

Radius of the bigger circle = 10 – 6 = 4cm

Ratio of areas will be square of the ration of radius which is 4:1.

Question 7: There are 12 points in a two-dimensional plane with following coordinates: Points A, B, C, D, E,F, G have coordinates (1, 0), (2, 0), (3, 0), (4, 0), (5, 0), (6, 0) and (7, 0) respectively. Points H, I, J havecoordinates (1, 1), (2, 2) and (3, 3) respectively. Points K, L have coordinates (4, -2) and (5, -3)respectively. The number of circles possible with these points are?

a) 179

b) 158

c) 168

d) 147

7) Answer (A)

Solution:

A, B, C, D, E, F, G all lie of a single line

H, I, J all lie on another single line

K, L lie on another single line

If we are given three points which are not collinear than we can draw a circle from these three points

Question 8: Two circles P and Q, each of radius 2 cm, pass through each other’s centres. They intersect at points A and B. A circle R is drawn with diameter AB. What is the area of overlap (in square cm) between the circles R and P?

a) $\frac{8 \pi}{3} – 2 \sqrt 3$

b) $\frac{8 \pi}{3}$

c) $\frac{13 \pi}{3} – \sqrt 3$

d) $\frac{17 \pi}{6} – 2 \sqrt 3$

e) $\frac{17 \pi}{6} – \sqrt 3$

8) Answer (E)

Solution:

We know that radius of circle P is 2 cm

Length of MO = 1 cm

radius of circle R = AO = $\sqrt{\ 2^2-1^2}$ = $\sqrt{\ 3}$

Area of overlap between the circle R and P(shaded region) = semi circle area of R + area of segment ANBOA

Area of segment ANBOA = area of sector ANBM – area of triangle AMB

= $\frac{120}{360}\pi\ \left(2\right)^2$ – $\frac{1}{2}\left(1\right)\left(2\sqrt{\ 3}\right)$

= $\frac{4\pi}{3}-\sqrt{\ 3}$

Area of overlap between circle R and P = $\frac{\pi\ \left(\sqrt{\ 3}\right)^2}{2}$+ $\frac{4\pi}{3}-\sqrt{\ 3}$

= $\ \frac{\ 17\pi\ }{6}-\sqrt{\ 3}$

Answer is option E.

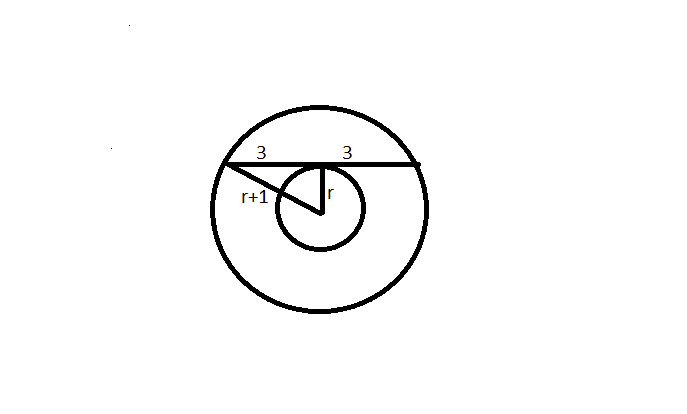
Question 9: Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6cm and is a tangent to C2, then the diameter, in cm, of C1 is

9) Answer: 10

View Video Solution

Solution:

Now we know that the perpendicular from the centre to a chord bisects the chord. Hence at the point of intersection of tangent, the chord will be divided into two parts of 3 cm each. As you can clearly see in the diagram, a right angled triangle is formed there.

Hence   $\left(r+1\right)^2=r^2+9$ or $r^{2\ }+1+2r\ =\ r^2+9\ or\ 2r=8\ or\ r=4cm$

Hence the radius of the larger circle is 5cm and diameter is 10cm.

Question 10: Mohanlal, a prosperous farmer, has a square land of side 2 km. For the current season, he decides to have some fun. He marks two distinct points on one of the diagonals of the land. Using these points as centers, he constructs two circles. Each of these circles falls completely within the land, and touches at least two sides of the land. To his surprise, the radii of both the circles are exactly equal to $\frac{2}{3}$ km. Mohanlal plants potatoes on the overlapping portion of these circles. Calculate the area on which Mohanlal planted potatoes (in sq. km).

a) $\frac{5(\pi + 4)}{27}$

b) $\frac{2(2 \pi – 3\sqrt{3})}{27}$

c) $\frac{(\pi – 2)}{9}$

d) $\frac{2(\pi – 2)}{9}$

e) $\frac{4(\pi – 3\sqrt{3})}{27}$

10) Answer (D)

Solution:

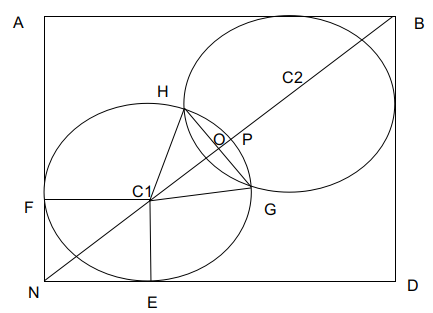
The two circles are symmetric about the diagonal.

NC1=$\frac{2\sqrt{\ 2}}{3}$ = $\sqrt{\ \left(\frac{2}{3}\right)^{^2}+\left(\frac{2}{3}\right)^2}=\ \frac{\left(2\sqrt{\ 2}\right)}{3}$

The lengths FC1, EC1 are the radius of the circle which is 2km/3.

The length C1P is the radius of the circle.

Because of symmetry C1O = C2O and C1N = C2B.

2*(C1N+ C1O) = $2\sqrt{\ 2}$ the length of the diagonal of the square.

C1N+C1O = $\sqrt{\ 2}$

C1O = $\sqrt{\ 2}-\frac{2\sqrt{\ 2}}{3}=\ \frac{\sqrt{\ 2}}{3}$

OP = $\frac{\left(2-\sqrt{\ 2}\right)}{3}$

The diagonal perpendicularly bisects the line GH. Hence C1OH is 90 degrees.$C1H^2\ =\ C1O^2+OH^2$

OH = $\frac{\sqrt{\ 2}}{3}$. Similarly OG = $\frac{\sqrt{\ 2}}{3}$

HC1, C1G both are equal to $\frac{2}{3}$ each. H1G is $\frac{2\sqrt{\ 2}}{3}$. HC1G is a raight angled traingle with angle HC1G is 90 degrees.

Area of the region required is 2*(Area of segment OGH)

.’. Area of required region=$2\left(\frac{90}{360}\cdot\frac{4\pi\ }{9}-\frac{1}{2}\cdot\frac{2\sqrt{\ 2}}{3}\cdot\frac{\sqrt{\ 2}}{3}\right)$=$\frac{2(\pi – 2)}{9}$

Question 11: A rectangular field is 40 meters long and 30 meters wide. Draw diagonals on this field and then draw circles of radius 1.25 meters, with centers only on the diagonals. Each circle must fall completely within the field. Any two circles can touch each
other but should not overlap. What is the maximum number of such circles that can be drawn in the field?

a) 38

b) 39

c) 36

d) 37

e) 40

11) Answer (D)

Solution:

Each circle on the end of the diagonal will touch sides of the rectangular field

Using Pythagoras’ theorem, the distance between the vertex of the rectangle and center of the first circle drawn on the diagonal = $1.25\sqrt{\ 2}$

Distance between the vertex of the rectangle and circumference of the first circle drawn on the diagonal = $1.25\sqrt{\ 2}$ – 1.25 = 0.51 meters

Space that cannot be used to draw circle otherwise they will go outside rectangle on every diagonal = 0.51 * 2 = 1.02 meters

Space that can be used to draw circles = length of diagonal – unused space = 50 – 1.02 = 48.98 meters

On every diagonal, maximum number of such circles = usable length/diameter of each circle = 48.98/2.5 = 19

Or, on every diagonal, one circle will be at the center (intersection of diagonals) and 9 circles will be on each half of the diagonal

.’. The circle in center will be common for both diagonals, and 9 circles can be drawn on each half of the diagonal. So total circles = 9*4 + 1 = 37

Question 12: A square of length 1 m is inside a square of length 2 m and four quarter circles are joined as shown in the figure. The value of y —x is given by,

a) $\frac{8-\pi}{10}$

b) $\frac{4-\pi}{5}$

c) $\frac{2\pi-1}{8}$

d) $\frac{\pi-3}{4}$

12) Answer (D)

Solution:

From the above figure area of  the region bounded by ABCDEFGH = Are of the square with side 2 – (4*quadrants with side 1cm + 4x)

=4-$\pi\ $-4x

Which is same as the area of the square with side 1 cm -4y

4-$\pi\ $-4x = 1-4y

4x-4y=3-$\pi$

y-x= $\frac{\pi-3}{4}$

D is the correct answer.

Question 13: Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is

a) $\frac{1}{\surd2}$

b) $\frac{\pi}{3}$

c) $\surd2$

d) 1

13) Answer (D)

View Video Solution

Solution:

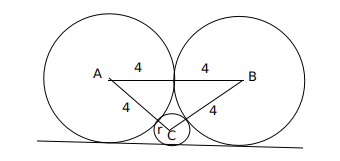
Let ‘h’ be the height of the triangle ABC, semiperimeter(S) $= \frac{4+4+r+4+4+r}{2} = 8+r$,
$a=4+r, b=4+r, c=8$

Area of triangle ABC $=\ \ \sqrt{\ s\cdot\left(s-a\right)\left(s-b\right)\left(s-c\right)}=$
$= \sqrt{\left(\ 8+r\right)\times\ 4\times\ 4\times\ r}$ = $\ \frac{\ 1}{2}\times\ \left(4+4\right)\times\ height$

Height (h) = $\sqrt{\ \left(8+r\right)r}$

Now, $ h + r = 4 \longrightarrow  \sqrt{\ \left(8+r\right)r} + r = 4$ (Considering the height of the triangle)

$\sqrt{\ \left(8+r\right)r}$=4-r

16r=16

r=1

Alternatively,

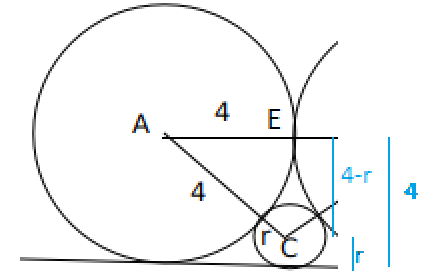
$\text{AE}^@+\text{EC}^2=\text{AC}^2 \longrightarrow 4^2+\left(4-r\right)^2 = \left(4+r\right)^2 \longrightarrow\ \longrightarrow\ \longrightarrow\ r=1$

Question 14: As shown in the figure, there is a square of 24 cm. A circle is inscribed inside the square. Inside the circle are four circles of equal radius which are inscribed. The total area of the shaded region in the figure given below is ________

a) 576 – 196 $\pi$

b) 584 – 196 $\pi$

c) 864 – 196 $\pi$

d) none of the above

14) Answer (D)

Solution:

The above area can be obtained by the following operation: Area of Big Square – Area of the Bigger circle + $4\times\ $ Area of Smaller Circle + $8\times\ $ Overlapping Area of smaller circles

i) Area of Big Square = $24\times\ 24=576$

ii) Area of Big circle = $\pi\ 12^2\ =\ 144\pi\ $

iii) Area of smaller circle = $\pi\ 6^2\ =\ 36\pi\ $

iv) For Area of smaller common area = 2b from below figure

Area b = Area of circular arc(2b+a) – Area of triangle (a+b)

= $\frac{1}{4}\left(36\pi\ \right)-\ \frac{1}{2}\left(6\times\ 6\right)$  =$9\pi\ -18$

Area of common part of smaller circle = 2b = $18\pi\ -36$

Therefore required area = $576-144\pi+\left(4\times\ 36\pi\right)-8\times\ \left(18\pi\ -36\right)$

= $288+144\pi\ $

None of the above are correct

Question 15: Let the equations of two circles $C_1$ and $C_2$ be given by $x^2 + y^2 – 4x – 4y + 6 = 0$ and $x^2 + y^2 – 10x – 10y + k = 0$ respectively, where $k$ is a constant. Suppose that $C_1$ and $C_2$ have exactly two common tangents. Then possible values of $k$ are

a) $0 < k < 18$

b) $18 < k < 42$

c) $42 < k < 50$

d) none of the above

15) Answer (B)

Solution:

Centre and radius of a circle $x^2 + y^2 +2gx +2fy + c = 0$ is (-g,-h) and $\sqrt{g^{2}+h^{2}-c}$
Centre and the radius of $C_1$ is (2,2) and $\sqrt{2}$
Centre and the radius of $C_2$ is (5,5) and $\sqrt{50-k}$
Distance between the centres of the two circles = $\sqrt{18}$
According to the properties of the circle
If two circles have two common tangents then ,
|Difference of the radii|  < Distance between the centres of the two circles < |Sum of the radii|
$\sqrt{50-k}$ – $\sqrt{2}$ <  $\sqrt{18}$ < $\sqrt{50-k}$ + $\sqrt{2}$
Let’s look at the options one by one ,

Option A : let k= 1  |7-$\sqrt{2}$| < 3$\sqrt{2}$ < |7+$\sqrt{2}$|  ——————->  Does not satisfy
Option B : let k= 25 |5-$\sqrt{2}$| < 3$\sqrt{2}$ < |5+$\sqrt{2}$|  ——————-> Satisfied
Option C : let k= 49  |1-$\sqrt{2}$| < 3$\sqrt{2}$ < |1+$\sqrt{2}$|  ——————->  Does not satisfy

Hence B is the correct answer.

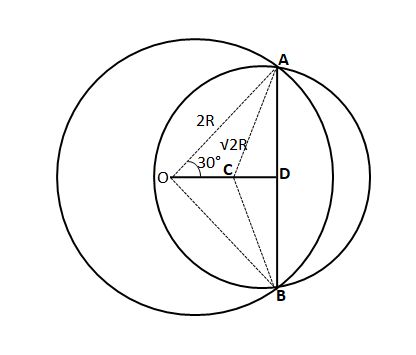
Question 16: Two circles with radius 2R and $\sqrt{2R}$ intersect each other at points A and B. The centers of both the circles are on the same side of AB. O is the center of the bigger circle and ∠AOB is 60°. Find the area of the common region between two circles.

a) $(\sqrt{3}-\pi-1)R^{2}$

b) $(\sqrt{3}-\pi)R^{2}$

c) $(\frac{13\pi}{6}+1-\sqrt{3})R^2$

d) $(\frac{13\pi}{6}+\sqrt{3})R^2$

e) None of the above

16) Answer (C)

Solution:

Let us draw the diagram according to the given info,

We can see that AD = AO*cos60° = 2R*$\dfrac{1}{2}$ = R

In triangle, ACD

$\Rightarrow$ $sinACD=\dfrac{AC}{AC}$

$\Rightarrow$ $sinACD=\dfrac{R}{\sqrt{2}*R}$ = $\dfrac{1}{\sqrt{2}}$

$\Rightarrow$ $\angle$ ACD = 45°

By symmetry we can say that $\angle$ BCD = 45°

Therefore we can say that $\angle$ ACB = 90°

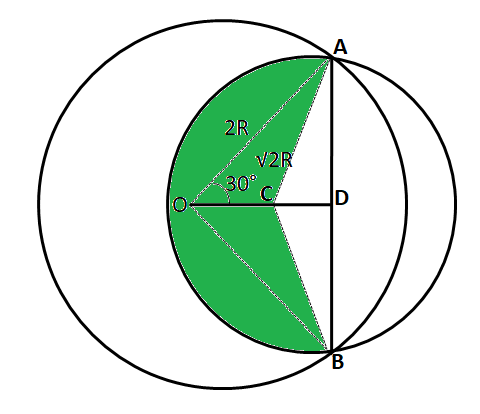
Hence, the area colored by green color = $\dfrac{270°}{360°}*\pi*(\sqrt{2}R)^2$ = $\dfrac{3}{2}*\pi*R^2$ … (1)

Area of triangle ACB = $\dfrac{1}{2}*R*2R$ = $R^2$ … (2)

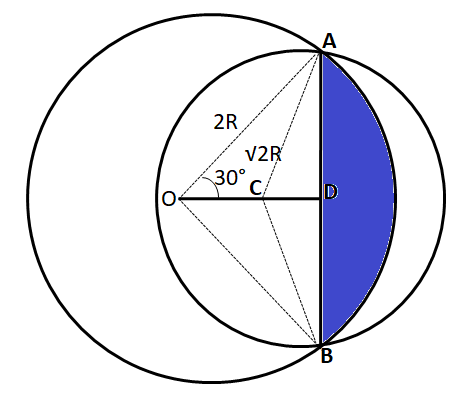
Area shown in blue color = $\dfrac{60°}{360°}*\pi*(2R)^2-\dfrac{\sqrt{3}}{4}*(2R)^2$ = $\dfrac{2}{3}*\pi*R^2-\sqrt{3}*R^2$ … (3)

By adding (1) + (2) + (3)

Therefore, the area of the common region between two circles = $\dfrac{3}{2}*\pi*R^2$ + $R^2$ + $\dfrac{2}{3}*\pi*R^2-\sqrt{3}*R^2$

$\Rightarrow$ $(\dfrac{13\pi}{6}+1-\sqrt{3})R^2$

Hence, option C is the correct answer.

Question 17: There are two circles $C_{1}$ and $C_{2}$ of radii 3 and 8 units respectively. The common internal tangent, T, touches the circles at points $P_{1}$ and $P_{2}$ respectively. The line joining the centers of the circles intersects T at X. The distance of X from the center of the smaller circle is 5 units. What is the length of the line segment $P_{1} P_{2}$ ?

a) ≤ 13

b) > 13 and ≤ 14

c) > 14 and ≤ 15

d) > 15 and ≤ 16

e) > 16

17) Answer (C)

Solution:

Given : $OP_1 = 3 , O’P_2 = 8 , OX = 5$ units

To find : $P_1P_2 = ?$

Solution : In $\triangle OP_1X$

=> $(P_1X)^2 = (OP_1)^2 – (OX)^2$

=> $(P_1X)^2 = 5^2 – 3^2 = 25 – 9$

=> $P_1X = \sqrt{16} = 4$

In $\triangle OP_1X$ and $\triangle O’P_2X$

$\angle OXP_1 = O’XP_2$   (Vertically opposite angles)

$\angle OP_1X = O’P_2X = 90$

=> $\triangle OP_1X \sim \triangle O’P_2X$

=> $\frac{XP_1}{XP_2} = \frac{OP_1}{O’P_2}$

=> $XP_2 = 4 \times \frac{8}{3} = 10.66$

$\therefore P_1P_2 = P_1X + XP_2 = 4 + 10.66 = 14.66$ units

Question 18: In the following figure, ACB is a right-angled triangle. AD is the altitude. Circles are inscribed within the triangle ACD and triangle BCD. P and Q are the centers of the circles. The distance PQ is

The length of AB is 15 m and AC is 20 m

a) 7 m

b) 4.5 m

c) 10.5 m

d) 6 m

18) Answer (A)

View Video Solution

Solution:

By Pythagoras theorem we get BC = 25 . Let BD = x;Triangle ABD is similar to triangle CBA => AD/15 = x/20 and also triangle ADC is similar to triangle ACB=> AD/20 = (25-x)/15. From the 2 equations, we get x = 9 and DC = 16

We know that AREA = (semi perimeter ) * inradius

For triangle ABD, Area = 1/2 x BD X AD = 1/2 x 12 x 9 = 54 and semi perimeter = (15 + 9 + 12)/2 = 18. On using the above equation we get, inradius, r = 3.

Similarly for triangle ADC we get inradius R = 4 .

PQ = R + r = 7 cm

Question 19: The length of the common chord of two circles of radii 15 cm and 20 cm, whose centres are 25 cm apart, is

a) 24 cm

b) 25 cm

c) 15 cm

d) 20 cm

19) Answer (A)

View Video Solution

Solution:

The radii of both the circles and the line joining the centers of the two circles form a right angled triangle. So, the length of the common chord is twice the length of the altitude dropped from the vertex to the hypotenuse.

Let the altitude be h and let it divide the hypotenuse in two parts of length x and 25-x
So, $h^2 + x^2 = 15^2$ and $h^2 + (25-x)^2 = 20^2$
=> $225 – x^2 = 400 – x^2 + 50x – 625$
=> 50x = 450 => x = 9 and h = 12
So, the length of the common chord is 24 cm.

Question 20: A jogging park has two identical circular tracks touching each other, and a rectangular track enclosing the two circles. The edges of the rectangles are tangential to the circles. Two friends, A and B, start jogging simultaneously from the point where one of the circular tracks touches the smaller side of the rectangular track. A jogs along the rectangular track, while B jogs along the two circular tracks in a figure of eight. Approximately, how much faster than A does B have to run, so that they take the same time to return to their starting point?

a) 3.88%

b) 4.22%

c) 4.34%

d) 4.46%

20) Answer (D)

View Video Solution

Solution:

Let the radius of 2 circles be r . Speed of A would be 12r/t and Speed of B would be 4*Pi*r/t . To find percentage faster B have to run than A we have : (4*Pi – 12)*100/ (4*Pi) = 4.46% approx. Hence, option D.

Take MAH-CET Mock Tests

Enroll to CAT 2022 course