Geometry Circle Questions for MAH-CET PDF

Here you can download the important MAH – CET Geometry Circle Questions PDF by Cracku. Very Important MAH – CET 2022 and These questions will help your MAH – CET preparation. So kindly download the PDF for reference and do more practice.

Download Geometry Circle Questions for MAH-CET PDF

Enroll to MAH-CET Crash Course

Question 1: A circle of diameter 8 inches is inscribed in a triangle ABC where $\angle ABC = 90^\circ$. If BC = 10 inches then the area of the triangle in square inches is

Question 2: Two circles P and Q, each of radius 2 cm, pass through each other’s centres. They intersect at points A and B. A circle R is drawn with diameter AB. What is the area of overlap (in square cm) between the circles R and P?

a) $\frac{8 \pi}{3} – 2 \sqrt 3$

b) $\frac{8 \pi}{3}$

c) $\frac{13 \pi}{3} – \sqrt 3$

d) $\frac{17 \pi}{6} – 2 \sqrt 3$

e) $\frac{17 \pi}{6} – \sqrt 3$

2) Answer (E)

Solution:

We know that radius of circle P is 2 cm

Length of MO = 1 cm

radius of circle R = AO = $\sqrt{\ 2^2-1^2}$ = $\sqrt{\ 3}$

Area of overlap between the circle R and P(shaded region) = semi circle area of R + area of segment ANBOA

Area of segment ANBOA = area of sector ANBM – area of triangle AMB

= $\frac{120}{360}\pi\ \left(2\right)^2$ – $\frac{1}{2}\left(1\right)\left(2\sqrt{\ 3}\right)$

= $\frac{4\pi}{3}-\sqrt{\ 3}$

Area of overlap between circle R and P = $\frac{\pi\ \left(\sqrt{\ 3}\right)^2}{2}$+ $\frac{4\pi}{3}-\sqrt{\ 3}$

= $\ \frac{\ 17\pi\ }{6}-\sqrt{\ 3}$

Answer is option E.

Question 3: Let C1 and C2 be concentric circles such that the diameter of C1 is 2cm longer than that of C2. If a chord of C1 has length 6cm and is a tangent to C2, then the diameter, in cm, of C1 is

Question 4: Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to

a) 8.8

b) 7.8

c) 6.6

d) 7.2

4) Answer (A)

View Video Solution

Solution:

We can form the following figure based on the given information:

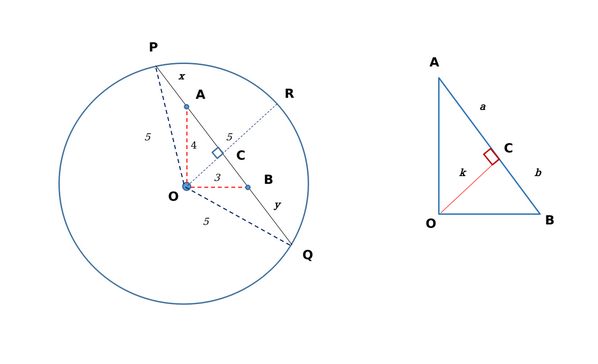
Since OA = 4 m and OB=3 m; AB = 5 m. OR bisects the chord into PC and QC.

Since AB = 5 m, we have $a+b = 5      …(i)$  Also, $4^2\ -k^2=a^2…\left(ii\right)$ and $3^2\ -k^2=b^2…\left(iii\right)$

Subtracting (iii) from (ii), we get: $a^2\ -b^2=7…\left(iv\right)$

Substituting (i) in (iv), we get $a – b = 1.4      …(v)$; $\left[\left(a+b\right)\left(a\ -b\right)=7;\ \therefore\ \left(a-b\right)=\frac{7}{5}\right]$

Solving (i) and (v), we obtain the value of $a=3.2$ and $b=1.8$

Hence, $k^2\ =\ 5.76$

Moving on to the larger triangle $\triangle\ POC$, we have $5^2-k^2=\left(x+a\right)^2$;

Substituting the previous values, we get: $(25-5.76)=\left(x+3.2\right)^2$

$\sqrt{19.24}=\left(x+3.2\right)$ or $x = 1.19 m$

Similarly, solving for y using $\triangle\ QOC$, we get $y=2.59 m$

Therefore, $PQ = 5+2.59+1.19 = 8.78 \approx\ 8.8 m$

Hence, Option A is the correct answer.

Question 5: The vertices of a triangle are (0,0), (4,0) and (3,9). The area of the circle passing through these three points is

a) $\frac{14\pi}{3}$

b) $\frac{123\pi}{7}$

c) $\frac{12\pi}{5}$

d) $\frac{205\pi}{9}$

5) Answer (D)

View Video Solution

Solution:

Equation of circle $x^2+y^2+2gx+2fy+c=0$

It passes through (0,0), (4,0) and (3,9). Substitute each point in the above equation:

=> On substituting the value (0,0) in the above equation, we obtain: $c=0$

=> On substituting the value (4,0) in the above equation, we obtain:  $16+0+8g+0 = 0$ ; $g=-2$

=> On substituting the value (3,9) in the above equation, we obtain: $9+81-12+18f = 0$ ; $f= -13/3$

Radius of the circle r = $\sqrt{\ g^2+f^2-c}$ => $r^2=\frac{205}{9}$

Therefore, Area = $\pi\ r^2=\frac{205\pi\ }{9}$

Take Free MAH-CET mock tests here

Question 6: A circle is inscribed in a rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is

a) $\frac{6\pi}{25}$

b) $\frac{5\pi}{18}$

c) $\frac{3\pi}{25}$

d) $\frac{2\pi}{15}$

6) Answer (A)

View Video Solution

Solution:

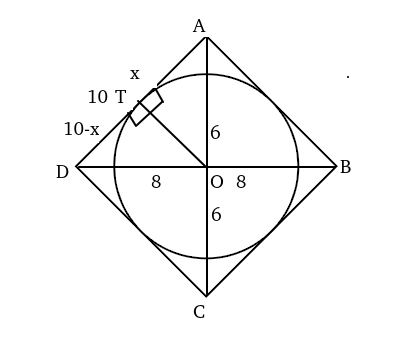
Let the length of radius be ‘r’.

From the above diagram,

$x^2+r^2=6^2\ $….(i)

$\left(10-x\right)^2+r^2=8^2\ $—-(ii)

Subtracting (i) from (ii), we get:

x=3.6 => $r^2=36-\left(3.6\right)^2$ ==> $r^2=36-\left(3.6\right)^2\ =23.04$.

Area of circle = $\pi\ r^2=23.04\pi\ $

Area of rhombus= 1/2*d1*d2=1/2*12*16=96.

.’. Ratio of areas = 23.04$\pi\ $/96=$\frac{6\pi}{25}$

Question 7: On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is

a) $3\sqrt{\pi}(5+\frac{12}{\pi})$

b) $4\sqrt{\pi}(3+\frac{9}{\pi})$

c) $3\sqrt{\pi}(\frac{5}{2}+\frac{6}{\pi})$

d) $5\sqrt{\pi}(3+\frac{9}{\pi})$

7) Answer (A)

View Video Solution

Solution:

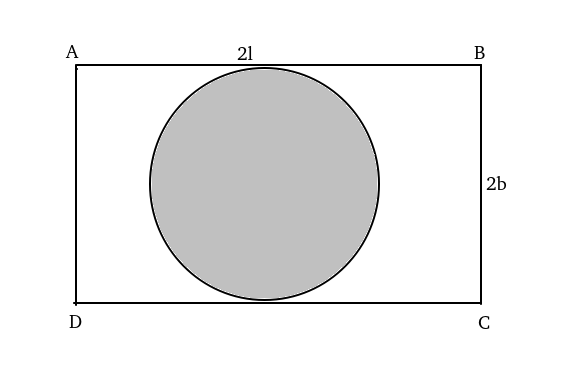
Let ABCD be the rectangle with length 2l and breadth 2b respectively.

Area of the circle i.e. area of painted region = $\pi\ b^2$.

Given, 4lb-$\pi\ b^2$=(2/3)$\pi\ b^2$.

=> 4lb=(5/3)$\pi\ b^2$.

=>l=$\frac{5\pi}{12}b$.

Given, 4lb=135 => 4*$\frac{5\pi}{12}b^2$=135 => b= $\frac{9}{\sqrt{\ \pi\ }}$

=> l=$\frac{15}{4}\sqrt{\ \pi\ }$
Perimeter of rectangle =4(l+b)=4($\frac{15}{4}\sqrt{\ \pi\ }$+$\frac{9}{\sqrt{\ \pi\ }}$ )=$3\sqrt{\pi}(5+\frac{12}{\pi})$.

Hence option A is correct.

Question 8: The locus of the centre of a circle that passes through the origin and cuts off a length 2a from the line y = c is

a) $x^2 + 2cx = a^2 + c^2$

b) $x^2 + 2cy = a^2 + c^2$

c) $y^2 + 2cx = a^2 + c^2$

d) $y^2 + 2cy = a^2 + c^2$

8) Answer (B)

Solution:

Let the locus of the center be represented by (h,k)

Since it passes through origin. Radius r = $\sqrt{\ h^2+k^2}$

Since it cuts off chord of length = 2a on y=c. We draw 1 perpendicular bisector of the chord till the center and make a line which is intersecting point of line y=c and the circle.

We obtain a right triangle that has “r” as its hypotenuse and a and |c-k| as its sides.

Applying Pythogoras theorm,

$r^2\ =\ a^2\ +\ \left(c-k\ \right)^2$

it implies

$h^2+k^2\ =\ a^2\ +\ \left(c-k\ \right)^2$

$h^2+k^2\ =\ a^2\ +\ c^2+k^2\ -2ck$

$h^2+2ck\ =\ a^2\ +\ c^2$

replacing (h,k) by (x,y)

we get $x^2+2cy\ =\ a^2\ +\ c^2$

Question 9: The radius of the incircle of the triangle formed by the x-axisand the lines 3x + 4y – 24 = 0, 3x – 4y + 24 = 0 is

a) $\frac{7}{3}$

b) $\frac{8}{3}$

c) $2$

d) $3$

9) Answer (B)

Solution:

For 3x+4y-24=0 can be re-written as $3x+4y=24$

=>$\frac{3x+4y\ \ }{24}=1$

=>$\ \frac{\ x}{8}+\ \frac{\ y}{6}=1$.

So, this becomes the equation of the straight line of the form $\ \frac{\ x}{a}+\ \frac{\ y}{b}=1$, where a and b are x and y intercepts respectively. The X and Y intercepts for this equation are 8 and 6 respectively.

Similarly 3x-4y+24=0 can be re-written as $\ \frac{\ x}{-8}+\ \frac{\ y}{6}=1$. The X and Y intercepts for this equation are 8 and -6 respectively.

So, we get the following triangle and the incircle can be drawn as:

So, the triangle has sides of length 10,10 and 16.

Area of the triangle= $\ \frac{\ 1}{2}\times\ Base\times\ Height$= $\ \frac{\ 1}{2}\times\ 16\times\ 6$= 48

We know that r*s= Area of the triangle, where r is the inradius and s is the semi-perimeter. s= $\ \frac{\ 1}{2}\left(16+10+10\right)$= 18

So, 18r= 48

=> Or, r= $\ \frac{\ 48}{18}=\ \ \frac{\ 8}{3}$

Question 10: The circle $x^2 + y^2 = 8$ intersects the parabola $y^2 = 2x$ at a point P in the first quadrant. The acute angle between the tangents to the circle and the parabola at the point P is

a) $\tan^{-1}(3)$

b) $\tan^{-1}(-3)$

c) $\tan^{-1}(\sqrt{3})$

d) $\tan^{-1}(-\sqrt{3})$

10) Answer (A)

Solution:

First, we will try and find the point of intersection of the two curves.

We do so by equating the two curves.

So, $x^2+\ y^2-8=y^2-2x$

=> $x^2+2x\ -8=0$

=> (x+4)(x-2)=0

=> x= -4 or 2.

But since, the point of intersection lies on the first quadrant, x=2.

By putting the value of x in any of the two curves, we can find the value of y.

‘.’ $y^2=2x$

=> $y^2=4$

=> y= 2 or -2. But the point of intersection is in first quadrant, so y=2.

So, P= (2,2)

Now, for the parabola $y^2=2x$, tangent can be found by differentiating the curve at (2,2).

=> $2y\ \frac{\ dy}{dx}=2$

=>$\frac{\ dy}{dx}=\ \frac{\ 1}{y}$

=> $\frac{\ dy}{dx}=\ \frac{\ 1}{2}$

.’. Angle made by the tangent to parabola at P, tan$\alpha\ $= $\ \frac{\ 1}{2}$.

Similarly, tangent at the circle $x^2+y^2=8$ can be found by differentiating the curve at (2,2)

=> $2x+2y\ \frac{\ dy}{dx}=0$

=> $2y\ \frac{\ dy}{dx}=-2x$

=> $\frac{\ dy}{dx}=\ \frac{\ -x}{y}$

=> $\frac{\ dy}{dx}=\ -1$.

.’. Angle made by the tangent to circle at P, tan$\beta\ $= -1

Now, the acute angle between the two tangents is represented by $\alpha\ -\beta\ $.

We will use the expression $\tan\left(\alpha-\beta\right)\ =\ \ \frac{\ \tan\ \alpha\ -\tan\ \beta\ }{1+\tan\ \alpha\ \tan\ \beta\ }$

=> $\tan\left(\alpha\ -\beta\ \right)=\ \ \frac{\ \ \frac{\ 1}{2}-\left(-1\right)}{1-\frac{\ 1}{2}}$

=>$\tan\left(\alpha\ -\beta\ \right)=\ \ \frac{\ \ \ \frac{\ 3}{2}}{\ \ \frac{\ 1}{2}}$

=>$\tan\left(\alpha\ -\beta\ \right)=\ \ 3$

.’. $\alpha\ -\beta\ =\ \ \tan^{-1}\left(3\right)$. therefore, option A

Question 11: Mohanlal, a prosperous farmer, has a square land of side 2 km. For the current season, he decides to have some fun. He marks two distinct points on one of the diagonals of the land. Using these points as centers, he constructs two circles. Each of these circles falls completely within the land, and touches at least two sides of the land. To his surprise, the radii of both the circles are exactly equal to $\frac{2}{3}$ km. Mohanlal plants potatoes on the overlapping portion of these circles. Calculate the area on which Mohanlal planted potatoes (in sq. km).

a) $\frac{5(\pi + 4)}{27}$

b) $\frac{2(2 \pi – 3\sqrt{3})}{27}$

c) $\frac{(\pi – 2)}{9}$

d) $\frac{2(\pi – 2)}{9}$

e) $\frac{4(\pi – 3\sqrt{3})}{27}$

11) Answer (D)

Solution:

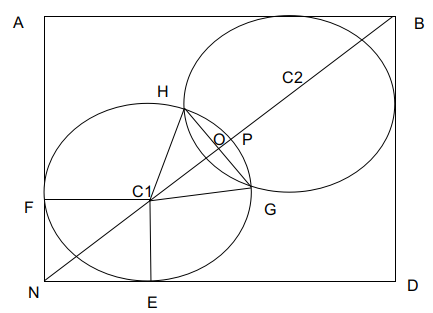
The two circles are symmetric about the diagonal.

NC1=$\frac{2\sqrt{\ 2}}{3}$ = $\sqrt{\ \left(\frac{2}{3}\right)^{^2}+\left(\frac{2}{3}\right)^2}=\ \frac{\left(2\sqrt{\ 2}\right)}{3}$

The lengths FC1, EC1 are the radius of the circle which is 2km/3.

The length C1P is the radius of the circle.

Because of symmetry C1O = C2O and C1N = C2B.

2*(C1N+ C1O) = $2\sqrt{\ 2}$ the length of the diagonal of the square.

C1N+C1O = $\sqrt{\ 2}$

C1O = $\sqrt{\ 2}-\frac{2\sqrt{\ 2}}{3}=\ \frac{\sqrt{\ 2}}{3}$

OP = $\frac{\left(2-\sqrt{\ 2}\right)}{3}$

The diagonal perpendicularly bisects the line GH. Hence C1OH is 90 degrees.$C1H^2\ =\ C1O^2+OH^2$

OH = $\frac{\sqrt{\ 2}}{3}$. Similarly OG = $\frac{\sqrt{\ 2}}{3}$

HC1, C1G both are equal to $\frac{2}{3}$ each. H1G is $\frac{2\sqrt{\ 2}}{3}$. HC1G is a raight angled traingle with angle HC1G is 90 degrees.

Area of the region required is 2*(Area of segment OGH)

.’. Area of required region=$2\left(\frac{90}{360}\cdot\frac{4\pi\ }{9}-\frac{1}{2}\cdot\frac{2\sqrt{\ 2}}{3}\cdot\frac{\sqrt{\ 2}}{3}\right)$=$\frac{2(\pi – 2)}{9}$

Question 12: XYZ is an equilateral triangle, inscribed in a circle. P is a point on the arc YZ such that X and P are on opposite sides of the chord YZ. Which of the following MUST always be true?

a) XZ + YP = XY + PZ

b) XP = XY

c) XP + PZ = XY + YP

d) XP = YP + PZ

e) XP = XY + YZ

12) Answer (D)

Solution:

If we join YP and PZ, XYPZ will become a cyclic quadrilateral. YZ and XP will be diagonals of this quadrilateral.

Ptolemy’s theorem states that the product of the length of the diagonals is equal to the sum of products of measures of the pairs of opposite sides.

As per this theorem for the quadrilateral :

XY*PZ +XZ*PY = YZ*XP.

For the equilateral triangle.

Now, in equilateral triangle XYZ, YZ = XZ = XY.

Hence equation 1 becomes, XP = YP + PZ.

Question 13: A rectangular field is 40 meters long and 30 meters wide. Draw diagonals on this field and then draw circles of radius 1.25 meters, with centers only on the diagonals. Each circle must fall completely within the field. Any two circles can touch each
other but should not overlap. What is the maximum number of such circles that can be drawn in the field?

a) 38

b) 39

c) 36

d) 37

e) 40

13) Answer (D)

Solution:

Each circle on the end of the diagonal will touch sides of the rectangular field

Using Pythagoras’ theorem, the distance between the vertex of the rectangle and center of the first circle drawn on the diagonal = $1.25\sqrt{\ 2}$

Distance between the vertex of the rectangle and circumference of the first circle drawn on the diagonal = $1.25\sqrt{\ 2}$ – 1.25 = 0.51 meters

Space that cannot be used to draw circle otherwise they will go outside rectangle on every diagonal = 0.51 * 2 = 1.02 meters

Space that can be used to draw circles = length of diagonal – unused space = 50 – 1.02 = 48.98 meters

On every diagonal, maximum number of such circles = usable length/diameter of each circle = 48.98/2.5 = 19

Or, on every diagonal, one circle will be at the center (intersection of diagonals) and 9 circles will be on each half of the diagonal

.’. The circle in center will be common for both diagonals, and 9 circles can be drawn on each half of the diagonal. So total circles = 9*4 + 1 = 37

Question 14: In the figure given below, the circle has a chord AB of length 12 cm, which makes an angle of $60^\circ$ at the center of the circle, O. ABCD, as shown in the diagram, is a rectangle. OQ is the perpendicular bisector of AB, intersecting the chord AB at P, the arc AB at M and CD at Q. OM = MQ. The area of the region enclosed by the line segments AQ and QB,and the arc BMA, is closest to (in cm$^2$):

a) 215

b) 137

c) 35

d) 63

e) 69

14) Answer (E)

Solution:

In triangle OAP, since AP=6, OA will be 12.

Area of AQBMA=Area of Triangle ABQ- (Area of minor arc AMB-Area of OAB)

Length of PQ=MQ+PM = 12+(12-$6\sqrt{\ 3}$)=24-$6\sqrt{\ 3}$

Area of Triangle ABQ=$\frac{1}{2}\cdot12.\left(24-6\sqrt{\ 3}\right)=6\left(24-6\sqrt{\ 3}\right)$.=81.64

Area of minor arc AMB-Area of OAB=$\frac{60}{360}\cdot\pi\ \cdot144-\frac{1}{2}\cdot12\cdot6\sqrt{\ 3}$ = $24\pi\ -36\sqrt{\ 3}$.=13.07

.’.Area of AQBMA=68.57$\approx\ 69$

Question 15: The radius of circle is so increased that its circumference increased by 5%. The area of the circle then increases by

a) 12.5%

b) 10.25%

c) 10.5%

d) 11.25%

15) Answer (B)

Solution:

We know that Circumference is dependent linearly on radius
so if circumference is increased by 5% , we can conclude radius is increased by 5%
Now Area varies directly with square of radius
Now if r is changed to 1.05 r
so r^2 will change to (1.05r)(1.05r) = 1.1025 r^2
So we can conclude area will change by 10.25%

Question 16: Let T be the triangle formed by the straight line 3x + 5y – 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is

Question 17: In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is

a) 2.5

b) 1.5

c) 3.5

d) 0.5

17) Answer (D)

View Video Solution

Solution:

In figure AE*BE=CE*DE    (The   intersecting chords theorem)

=> 7*15= x(20.5-x)                  (Assuming AE=x)

=> 210=x(41-2x)

=> $2x^2$-41x+210=0

=> x=10 or x=10.5   => AE=10 or AE=10.5      Hence BE = 20.5-10=10.5  or BE = 20.5-10.5=10

Required difference= 10.5-10=0.5

Question 18: AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to

a) 9.3

b) 7.8

c) 9.1

d) 8.5

18) Answer (C)

View Video Solution

Solution:

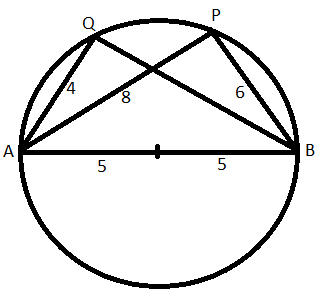
Since AB is a diameter,  AQB and APB will right angles.

In right triangle APB, AP = $\sqrt{10^2-6^2}=8$

Now, 2AQ=AP  => AQ= 8/2=4

In right triangle AQB, AP = $\sqrt{10^2-4^2}=9.165$ =9.1 (Approx)

Question 19: In the following diagram there are four semi circular arcs and a shaded region. The diameter of largest semi circle is 28cm and of the smallest is 7cm. The area of shaded region is

a) $98.75   \pi$

b) $120.5  \pi$

c) $105.5  \pi$

d) $110.25  \pi$

19) Answer (D)

Solution:

we have :

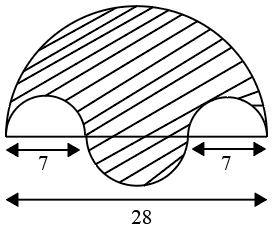
28-7-7 =14
So we have 4 semicircles with diameters 28,7,7 and 14 .
Now area of shaded region = Area of bigger semicircle (radius 14 ) – 2 (Area of smaller semicircles with radius 3.5 ) +Area of semicircle with radius 7
we get $\pi\ \ \frac{14^2}{2}-\ 2\ \frac{\pi\left(3.5\right)^2}{2}+\pi\ \ \frac{\left(7\right)^2}{2}$
= $98\pi+24.5\pi\ -12.25\pi\ \ =110.25\pi\ $

Question 20: A square of length 1 m is inside a square of length 2 m and four quarter circles are joined as shown in the figure. The value of y —x is given by,

a) $\frac{8-\pi}{10}$

b) $\frac{4-\pi}{5}$

c) $\frac{2\pi-1}{8}$

d) $\frac{\pi-3}{4}$

20) Answer (D)

Solution:

From the above figure area of  the region bounded by ABCDEFGH = Are of the square with side 2 – (4*quadrants with side 1cm + 4x)

=4-$\pi\ $-4x

Which is same as the area of the square with side 1 cm -4y

4-$\pi\ $-4x = 1-4y

4x-4y=3-$\pi$

y-x= $\frac{\pi-3}{4}$

D is the correct answer.

Take MAH-CET Mock Tests

Enroll to CAT 2022 course