Functions and Graphs Questions for IIFT PDF
Download important IIFT Functions and Graphs Questions PDF based on previously asked questions in IIFT and other MBA exams. Practice Functions and Graphs Questions and answers for IIFT and other exams.
Download Functions and Graphs Questions for IIFT PDF
Get 5 IIFT mock tests for Rs. 299. Enroll here
Download IIFT Previous Papers PDF
Take IIFT Mock Tests (With Solutions)
Question 1: A function $f (x)$ satisfies $f(1) = 3600$, and $f (1) + f(2) + … + f(n) =n^2f(n)$, for all positive integers $n > 1$. What is the value of $f (9)$ ?
a) 80
b) 240
c) 200
d) 100
e) 120
Instructions
Directions for the next 3 questions:
Given below are three graphs made up of straight-line segments shown as thick lines. In each case choose the answer as:
a) if f(x)=3f(-x)
b) if f(x)= -f(-x)
c) if f(x) = f(-x)
d) if 3f(x) = 6f(-x), for x >= 0
Question 2: 
a) if f(x)=3f(-x)
b) if f(x)= -f(-x)
c) if f(x) = f(-x)
d) if 3f(x) = 6f(-x), for x >= 0
Question 3:
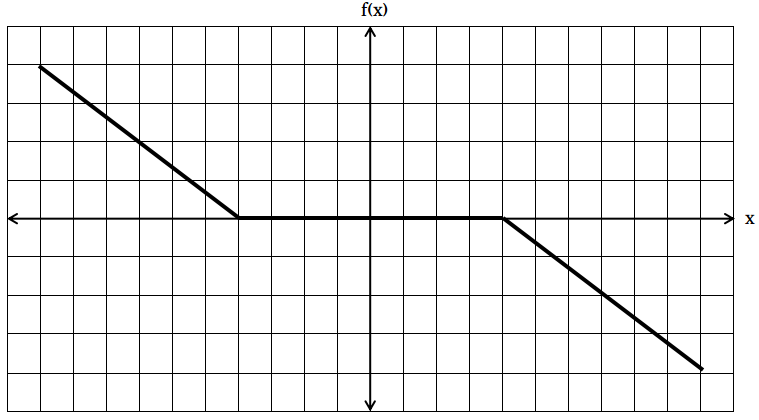
a) if f(x)=3f(-x)
b) if f(x)= -f(-x)
c) if f(x) = f(-x)
d) if 3f(x) = 6f(-x), for x >= 0
Instructions
DIRECTIONS for the following questions: These questions are based on the situation given below: In each of the questions a pair of graphs F(x) and F1(x) is given. These are composed of straight-line segments, shown as solid lines, in the domain $x\epsilon (-2, 2)$.
choose the answer as
a. If F1(x) = – F(x)
b. if F1(x) = F(- x)
c. if F1(x) = – F(- x)
d. if none of the above is true
Question 4: 
a) a
b) b
c) c
d) d
Question 5: 
a) a
b) b
c) c
d) d
Question 6: 
a) a
b) b
c) c
d) d
Question 7: 
a) a
b) b
c) c
d) d
Question 8: Let $f(x)\neq0$ for any ‘x’ be a function satisfying $f(x)f(y) = f(xy)$ for all real x, y. If $f(2) = 4$, then what is the value of $f(\frac{1}{2})$?
a) 0
b) 1/4
c) 1/2
d) 1
e) cannot be determined
Question 9: The function f(x) = |x – 2| + |2.5 – x| + |3.6 – x|, where x is a real number, attains a minimum at
a) x = 2.3
b) x = 2.5
c) x = 2.7
d) None of the above
Instructions
Directions for the following two questions:
Answer the questions on the basis of the information given below.
$f_1(x) = x$ if $0 \leq x \leq 1$
$f_1(x) = 1$ if x >= 1
$f_1(x) = 0$ otherwise
$f_2(x) = f_1(-x)$ for all x
$f_3(x) = -f_2(x)$ for all x
$f_4(x) = f_3(-x)$ for all x
Question 10: How many of the following products are necessarily zero for every x:$f_1(x)f_2(x), f_2(x)f_3(x), f_2(x)f_4(x)$
a) 0
b) 1
c) 2
d) 3
Get Complete MBA Test Series for Rs. 799
Answers & Solutions:
1) Answer (A)
According to given conditions we get f(2)=f(3)/3 , then f(3)=f(1)/6, then f(4)=f(1)/10 , then f(5)=f(1)/15 .
We can see the pattern here that the denominator goes on increasing from 3,3+3,6+4,10+5,15+6,.. so for the f(9) the denominator will be same as 15+6+7+8+9=45 .
So f(9)=3600/45 = 80
2) Answer (D)
In this graph, f(-1) = 1 and f(1) = 2 and since the two lines pass origin, their values increase linearly.
3f(x) = 6f(-x)
3) Answer (B)
In this graph, we can see that the graph on LHS of y axis is symmetrical to the graph on RHS of y axis about origin.
Hence f(x) = -f(-x)
4) Answer (D)
The correct relation between the two is: F(x) = | F1(x) |
So, all the three options a), b) and c) can be ruled out. Option d) is the correct answer.
5) Answer (B)
The value of F(x) for x < 0 is the same as the value of F1(x) for x > 0.
So, F1(x) = F(-x)
Option b) is the correct answer.
Take IIFT Mock Tests (With Solutions)
6) Answer (B)
The value of F(x) for x > 0 is the same as the value of F1(x) for x < 0.
So, F1(x) = F(-x)
Option b) is the correct answer.
7) Answer (C)
F(0) = 1 ; F1(0) = -1
F(1) = 0 ; F1(-1) = 0
F(2) = -1 ; F1(-2) = 1
=> F1(x) = -F(-x).
8) Answer (B)
$f(1)^2$ = f(1) => f(1) = 1
f(2)*(f(1/2) = f(1) => 4x = 1
So, f(1/2) = 1/4
9) Answer (B)
f(x) = |x – 2| + |2.5 – x| + |3.6 – x|
For x belonging to (-infinity to 2), f(x) = 2-x + 2.5-x + 3.6-x = 8.1-3x
This attains the minimum value at x=2. Value = 2.1
For x belonging to (2 to 2.5), f(x) = x-2 + 2.5-x + 3.6-x = 4.1-x
Attains the minimum value at x = 2.5. Value = 1.6
For x belonging to (2.5 to 3.6), f(x) = x-2 + x-2.5 + 3.6-x = x-0.9
Attains the minimum at x=2.5, value = 1.6
For x > 3.6, f(x) = x-2+x-2.5+x-3.6 = 3x – 8.1
Attains the minimum at x= 3.6, value = 2.7
So, min value of the function is 1.6 at x=2.5
10) Answer (C)
Checking for different values of x . Suppose x= -0.5 we get
$f_1(x)f_2(x) = 0*0.5 = 0$
$f_2(x)f_4(x) = 0.5*0 = 0$ .
But $f_2(x)f_3(x)$ is not equal to zero.
Hence two functions are necessarily equal to zero and two products given above are equal to zero.
IIFT Previous year question papers PDF
We hope this Functions and Graphs questions and answers for IIFT PDF will be helpful to you.
