Fraction Questions For SSC GD PDF
SSC GD Constable Fractions Question paper with answers download PDF based on SSC GD exam previous papers. 40 Very important Fractions questions for GD Constable.
DOWNLOAD FRACTION QUESTIONS FOR SSC GD PDF
GET 20 SSC GD MOCK FOR JUST RS. 117
Download SSC GD Important Questions PDF
1500+ Must Solve Questions for SSC Exams (Question bank)
Fraction Questions For SSC GD PDF[/shortlink]Question 1: If a:b=4:5, b:c=6:7, c:d=5:8 then what is the value of a:b:c:d ?
a) 24:30:28:32
b) 24:30:42:56
c) 24:30:35:49:
d) 24:30:35:56
Question 2: $\frac{75\times75-26\times26}{101}=?$
a) 59
b) 39
c) 29
d) 49
Question 3: If m = 9 and n = $\frac{1}{3}\ $m, then $\ \sqrt{(m)^{2}-(n)^{2}=?}$
a) $2\sqrt2$
b) $6\sqrt2$
c) $4\sqrt2$
d) $5\sqrt2$
Question 4: What should come in place of both the question marks (?) in the following equation. $\frac{16}{?}=\frac{?}{42.25}$
a) 2.6
b) 260
c) .26
d) 26
Question 5: $\frac{3}{4}\ $of $\ \frac{1}{7}\ $of a number 120, then the number
a) 1120
b) 560
c) 280
d) 140
Download SSC GD FREE PREVIOUS PAPERS
Question 6: By how much is $\ \frac{3}{5}$th of 75 greater than $\ \frac{4}{7}$th of 77?
a) 0
b) 5
c) 1
d) None of these
Question 7: $\frac{(a-b)^{2}}{(b-c) (c-a)}+\frac{(b-c)^{2}}{(a-b) (c-a)}+\frac{(a-c)^{2}}{(a-b) (b-c)}$, $a\neq b\neq c$ is
a) 0
b) 1
c) 2
d) 3
Question 8: If sum of two number be a and their product be, b, then the sum of their reciprocals is
a) $\frac{1}{a}+\frac{1}{b}$
b) $\frac{b}{a}$
c) $\frac{a}{b}$
d) $\frac{1}{ab}$
Question 9: If x = 3-2√2, then √x + (1/√x) is equal to ____.
a) 0
b) 1
c) 2
d) 2√2
Question 10: If x=y=z, then $\ \frac{(x+y+z)^{2}}{x^{2}+y^{2}+z^{2}}\ $is:
a) 2
b) 3
c) 1
d) 4
Question 11: If $\ \sqrt{y}\ $= 4x, then $\ \frac{x^{2}}{y}\ $is:
a) $\frac{1}{16}$
b) $\frac{1}{4}$
c) 4
d) 2
Question 12: Length of each edge of a regular tetrahedron is 1 cm. Its volume is:
a) $\frac{1}{4}\sqrt{3}\ $cu.cm
b) $\frac{\sqrt{2}}{6}\ $cu.cm
c) $\frac{1}{12}\sqrt{2}\ $cu.cm
d) $\frac{\sqrt{3}}{12}\ $cu.cm
Question 13: The Vulgar fraction of 0.3939…… is:
a) $\frac{11}{39}$
b) $\frac{17}{39}$
c) $\frac{13}{33}$
d) $\frac{15}{33}$
Question 14: If $a^2+b^2+c^2-ab-bc-ca=0$ then a:b:c is:
a) 1 : 1 : 2
b) 1 : 1 : 1
c) 1 : 2 : 1
d) 2 : 1 : 1
Question 15: If $a+\frac{1}{b}-1$ and $b+\frac{1}{c}-1$, then $c+\frac{1}{a}$ is equal to:
a) 0
b) 1
c) 2
d) $\frac{1}{2}$
Question 16: If $\alpha + \beta = 90^\circ$ then the expression $tan \alpha + Sin^2 \alpha + Sin^2 \beta$ is equal to: $tan \beta$
a) $Sec^2 \beta$
b) $tan^2 \beta$
c) $Sec^2 \alpha$
d) $tan^2 \alpha$
Question 17: Two positive whole numbers are such that the sum of the first and twice the second number is 8 and their difference is 2. The numbers are:
a) 7,5
b) 6,4
c) 3,5
d) 4,2
Question 18: If Cos A + Sin A = $\sqrt{2}$ Cos A then Cos A- Sin A is equal to: (Where $0^\circ$<A<$90^\circ$)
a) $\sqrt{2SinA}$
b) $\sqrt{SinA}$
c) $\sqrt{2}Sin A$
d) 2 Sin A
Question 19: If $\frac{a}{b}=\frac{c}{d}=5$, then $\frac{3a+4c}{3b+4d}$ is equal to
a) 60
b) 15
c) 5
d) 20
Question 20: The graph of linear equation y = x passes through the point
a) $\left(\begin{array}{c}0,\frac{3}{2}\end{array}\right)$
b) (1,1)
c) $\left(\begin{array}{c}-\frac{1}{2},\frac{1}{2}\end{array}\right)$
d) $\left(\begin{array}{c}\frac{3}{2},-\frac{3}{2}\end{array}\right)$
Question 21: Arrangement of the factions $\frac{4}{3},-\frac{2}{9},-\frac{7}{8},\frac{5}{12}$ into ascending order are
a) $-\frac{7}{8},-\frac{2}{9},\frac{5}{12},\frac{4}{3}$
b) $-\frac{2}{9},-\frac{7}{8},\frac{5}{12},\frac{4}{3}$
c) $-\frac{2}{9},-\frac{7}{8},\frac{4}{3},\frac{5}{12}$
d) $-\frac{7}{8},-\frac{2}{9},\frac{4}{3},\frac{5}{12}$
Question 22: If $2x^2+2y^2=4a$, then find the value of $\frac{2a}{x^2-a}+\frac{2a}{y^2-a}$
a) 0
b) 1
c) a
d) 2a
Question 23: Find the value of $n+n+\frac{3n}{2}+\frac{9n}{4}+………\infty$
a) 0
b)
c) 2
d) Infinity
Question 24: Find the value $((49)^\frac{3}{2}+(49)^\frac{-3}{2})$
a) 117549/343
b) 117550/343
c) 117649/343
d) 117650/343
Question 25: If $(\frac{3}{2})X=(\frac{5}{7})Y=(\frac{6}{5})Z$, then what is X:Y:Z ?
a) 105 : 50 : 84
b) 24 : 25 : 32
c) 15 : 21 : 25
d) 20 : 42 : 25
Question 26: Find the y-intercept of the line joining two points (1, 3) and (3, 5).
a) -2
b) 0
c) 2
d) 4
Question 27: What is the total length intercepted between both the axes by the line 8x+4y=40?
a) 5
b) 10
c) 15
d) 20
Question 28: From which of the following quadrants does the line 7x + 12y = 16 will pass?
a) I and II
b) II and III
c) I, II, III
d) I, II, IV
Question 29: The sum of a fraction and its reciprocal is $\frac{113}{56}$. Find the fraction.
a) $\frac{7}{8}$
b) $\frac{5}{8}$
c) $\frac{8}{9}$
d) $\frac{3}{7}$
Question 30: Manish can complete a work in 21 days and Karan can complete the same work in 28 days. If both together work for 7 days, then what fraction of total work is left?
a) $\frac{3}{5}$
b) $\frac{2}{3}$
c) $\frac{7}{12}$
d) $\frac{5}{12}$
Question 31: The equation of a line is given by 4y-6x+9=0. Find the slope of other line which is perpendicular to it.
a) $\frac{-2}{3}$
b) $\frac{2}{3}$
c) $\frac{3}{2}$
d) $\frac{-3}{2}$
Question 32: Arrange the fractions $\frac{3}{4},\frac{5}{12},\frac{13}{16},\frac{16}{29},\frac{3}{8}$ in their descending order of magnitude.
a) $\frac{3}{4}>\frac{3}{8}>\frac{13}{16}>\frac{16}{29}>\frac{5}{12}$
b) $\frac{3}{8}>\frac{5}{12}>\frac{16}{29}>\frac{3}{4}>\frac{13}{16}$
c) $\frac{13}{16}>\frac{3}{4}>\frac{16}{29}>\frac{5}{12}>\frac{3}{8}$
d) $\frac{13}{16}>\frac{16}{29}>\frac{3}{4}>\frac{5}{12}>\frac{3}{8}$
Question 33: Determine the value of $\frac{x+y}{x+2y}$ when $\frac{2x+y}{x+4y}=3$
a) $\frac{3}{5}$
b) $\frac{7}{10}$
c) $\frac{4}{5}$
d) $\frac{10}{9}$
Question 34: If $(x+1)$ is a factor of $x^2 -7qx+12q=0$, then find the possible values of $q$.
a) $-(\frac{1}{19})$
b) $-19$
c) $\frac{1}{19}$
d) $19$
Question 35: $\frac{9}{15}$ of $\frac{7}{3}$ of a number is greater than $\frac{7}{12}$ of $\frac{3}{5}$ of the same number by 7. Find the number.
a) 6.36
b) 6.67
c) 5.67
d) 5.36
Question 36: Divya and Kriti have total 46 candies. If Divya has 10 candies more than kriti, then find the total number of candies Divya have?
a) 20
b) 24
c) 28
d) 32
Question 37: If $\frac{-5x}{3}+2=x-6$, then fond the value of ‘x’.
a) 1
b) 2
c) 3
d) 4
Question 38: The sum of a proper fraction and its reciprocal is $\frac{61}{30}$. Find the fraction.
a) $\frac{1}{3}$
b) $\frac{5}{6}$
c) $\frac{3}{10}$
d) $\frac{3}{5}$
Question 39: If Y:X:Z=4:5:6, then find the value of $\frac{X-Y+Z}{X+Y-Z}$.
a) $\frac{3}{3}$
b) $\frac{3}{7}$
c) $\frac{5}{7}$
d) $\frac{7}{3}$
Question 40: If $X+\frac{4}{X}=4$, then find the value of $X^6+1$.
a) 51
b) 65
c) 78
d) 82
Answers & Solutions:
1) Answer (D)
Given a:b=4:5
b:c=6:7
First equate ‘b’ term of both the ratios then a:b=24:30 and b:c=30:35
Now we get a:b:c=24:30:35
Since c:d=5:8
To make c=35 multiply it with 7
So c:d becomes 35:56
$\therefore$ a:b:c:d=24:30:35:56
2) Answer (D)
$\frac{75\times75-26\times26}{101}$ = $ \frac{75^{2}-26^{2}}{101}$
==>$ \frac{(75+26)(75-26)}{101}$ ( $\because a^{2}-b^{2}=(a+b)(a-b)$)
= $\frac{101\times49}{101} = 49$
3) Answer (B)
Given : $m=9$ and $n=\frac{1}{3}m$
=> $n=\frac{1}{3}\times9=3$
To find : $\sqrt{(m)^{2}-(n)^{2}}$
= $\sqrt{(9)^2-(3)^2}$
= $\sqrt{81-9}=\sqrt{72}=6\sqrt2$
=> Ans – (B)
4) Answer (D)
$\frac{16}{x}=\frac{x}{42.25}$
==> $x^{2}=\frac{16\times4225}{100}$
==> $x=\frac{4\times65}{10}$
$\therefore x = 26$
5) Answer (A)
Let the number be ‘x’
$\frac{3}{4}\times\frac{1}{7}\times x$ = 120
x = $\frac{120\times7\times4}{3}$
$\therefore$ x = 1120
6) Answer (C)
$\frac{3}{5}\times75$ = 45
$\frac{4}{5}\times 77$ = 44
$\therefore$ 45 is greater than 44 by 1
7) Answer (D)
Let a=3, b=2, c=1
$\frac{(a-b)^{2}}{(b-c) (c-a)}+\frac{(b-c)^{2}}{(a-b) (c-a)}+\frac{(a-c)^{2}}{(a-b) (b-c)}$
= $\frac{(3-2)^{2}}{(2-1) (1-3)}+\frac{(2-1)^{2}}{(3-2) (1-3)}+\frac{(3-1)^{2}}{(3-2) (2-1)}$
= -$\frac{1}{2}-\frac{1}{2}$+4=3
8) Answer (C)
Let the two numbers be x and y
Given x+y=a
xy=b
$\frac{1}{x}+\frac{1}{y}$=?
$\frac{1}{x}+\frac{1}{y}$=$\frac{x+y}{xy}$=$\frac{a}{b}$
9) Answer (D)
Given, $x = 3-2\sqrt{2}$……(1)
$\sqrt{x} = \sqrt{3-2\sqrt{2}}$ (or) $\sqrt{x} = \sqrt{(\sqrt{2})^{2} + (\sqrt{1})^{2} -2\sqrt{2}}$
$\sqrt{x} = \sqrt{(\sqrt{2}) – \sqrt{1})^{2}}$ (or) $\sqrt{x} = {\sqrt{2} – 1}$……..(2)
Now, $\sqrt{x} + \frac{1}{\sqrt{x}}$ = $\frac{x + 1}{\sqrt{x}}$
Substitute equation (1) and (2) in the above equation
$\frac{3 – 2\sqrt{2} + 1}{\sqrt{2} – 1}$ (or) $\frac{4 – 2\sqrt{2}}{\sqrt{2} – 1}$
Multiply and divide by $\sqrt{2} + 1$
$\Rightarrow \frac{4 – 2\sqrt{2}}{\sqrt{2} – 1}$ x $\frac{\sqrt{2}+1}{\sqrt{2}+1}$ = $(4 – 2\sqrt{2})(\sqrt{2}+1)$
$\Rightarrow$ $(4\sqrt{2} + 4 – 4 -2\sqrt{2})$ = $2\sqrt{2}$
Hence, option D is the correct answer.
10) Answer (B)
Given : $x=y=z$
Let $x=y=z=k$
To find : $\ \frac{(x+y+z)^{2}}{x^{2}+y^{2}+z^{2}}\ $
= $\frac{(k+k+k)^2}{k^2+k^2+k^2}$
= $\frac{(3k)^2}{3k^2}$
= $\frac{9k^2}{3k^2}=3$
=> Ans – (B)
11) Answer (A)
Given : $\sqrt{y}=4x$
Squaring both sides, we get :
=> $y=16x^2$
=> $\frac{x^2}{y}=\frac{1}{16}$
=> Ans – (A)
12) Answer (C)
Side of tetrahedron = 1 cm
Volume of tetrahedron = $\frac{\sqrt2}{12}a^3$
= $\frac{\sqrt2}{12}(1)^3$
= $\frac{1}{12}\sqrt{2}\ $cu.cm
=> Ans – (C)
13) Answer (C)
Number = $0.\overline{39}$
Let $x=0.\overline{39}$ ————(i)
=> $100x=39.\overline{39}$ ————(ii)
Subtracting equation (i) from (ii),
=> $100x-x=39.39-0.39$
=> $99x=39$
=> $x=\frac{39}{99}=\frac{13}{33}$
=> Ans – (C)
14) Answer (B)
Given : $a^2+b^2+c^2-ab-bc-ca=0$
Multiplying both sides by 2, we get :
=> $2a^2+2b^2+2c^2-2ab-2bc-2ca=0$
=> $(a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ca+a^2)=0$
=> $(a-b)^2+(b-c)^2+(c-a)^2=0$
$\because$ Sum of three positive sum is 0, then each term is equal to ‘0’
=> $(a-b)=(b-c)=(c-a)=0$
=> $a=b=c$
$\therefore$ $a:b:c=1:1:1$
=> Ans – (B)
15) Answer (E)
16) Answer (E)
17) Answer (D)
Let the numbers be $x$ and $(x-2)$
According to ques,
=> $x+2(x-2)=8$
=> $x+2x-4=8$
=> $3x=8+4=12$
=> $x=\frac{12}{3}=4$
$\therefore$ Numbers are = 4, 2
=> Ans – (D)
18) Answer (C)
Given : $cos A+sin A=\sqrt2 cos A$
Squaring both sides, we get :
=> $(cos A+sin A)^2=(\sqrt2 cos A)^2$
=> $cos^2A+sin^2A+2sin A.cos A=2cos^2A$
=> $1+2sin A.cos A=2(1-sin^2A)$
=> $1+2sin A.cos A=2cos=2-2sin^2A$
=> $2sin A.cos A=2cos=1-2sin^2A$ —————–(i)
To find : $cos A-sin A=x$
Squaring both sides, we get :
=> $x^2=cos^2A+sin^2A-2sin A.cos A$
Substituting value from equation (i),
=> $x^2=1-(1-2sin^2A)$
=> $x^2=2sin^2A$
=> $x=\sqrt{2sin^2A}$
=> $x=\sqrt2sin A$
=> Ans – (C)
19) Answer (C)
Given : $\frac{a}{b}=\frac{c}{d}=5$
Let $a=c=5$ and $b=d=1$
To find : $\frac{3a+4c}{3b+4d}$
= $\frac{3(5)+4(5)}{3(1)+4(1)}$
= $\frac{15+20}{3+4}$
= $\frac{35}{7}=5$
=> Ans – (C)
20) Answer (B)
Only option B satisfies the given equation i.e
After substituting x=1 and y=1 in the given equation we get LHS equal to RHS.
Hence, option B is the correct answer.
21) Answer (A)
Given factions $\frac{4}{3},-\frac{2}{9},-\frac{7}{8},\frac{5}{12}$
Multiply 72(LCM) with each fraction, then we get
96, -16, -63, 30
Arrange them in ascending order i.e $-63 < -16 < 30 < 96$ (or) $-\frac{7}{8}<-\frac{2}{9}<\frac{5}{12}<\frac{4}{3}$
Hence, option A is the correct answer.
22) Answer (A)
Given : $2x^2+2y^2=4a$
=> $x^2+y^2=2a$ ———–(i)
To find : $\frac{2a}{x^2-a}+\frac{2a}{y^2-a}$
= $2a(\frac{1}{x^2-a}+\frac{1}{y^2-a})$
= $2a(\frac{(x^2-a)+(y^2-a)}{(x^2-a)(y^2-a)})$
= $2a(\frac{(x^2+y^2)-2a}{(x^2-a)(y^2-a)})$
Substituting value from equation (i), we get :
= $2a\times\frac{2a-2a}{(x^2-a)(y^2-a)}$
= $2a\times0=0$
=> Ans – (A)
23) Answer (D)
Expression = $n+n+\frac{3n}{2}+\frac{9n}{4}+………\infty$
= $n+(n+\frac{3n}{2}+\frac{9n}{4}+………\infty)$
It is a geometric progression with common ratio, $r=\frac{3}{2}$ and first term, $a=n$
$\because$ The common ratio is greater than 1, => Sum will tend to infinity.
=> Ans – (D)
24) Answer (C)
Expression = $((49)^\frac{3}{2}+(49)^\frac{-3}{2})$
= $((7^2)^{\frac{3}{2}}+(7^2)^{\frac{-3}{2}})$
= $7^3+7^{-3}$
= $343+\frac{1}{343}$
= $\frac{117649}{343}$
=> Ans – (C)
25) Answer (D)
Let $(\frac{3}{2})X=(\frac{5}{7})Y=(\frac{6}{5})Z=k$
=> $X=\frac{2k}{3}$, $Y=\frac{7k}{5}$ and $Z=\frac{5k}{6}$
=> $X:Y:Z=\frac{2k}{3}:\frac{7k}{5}:\frac{5k}{6}$
Multiplying the terms by L.C.M. (3,5,6) = 30
=> $30(\frac{2}{3}:\frac{7}{5}:\frac{5}{6})$
= $20:42:25$
=> Ans – (D)
26) Answer (C)
Equation of line joining points $(x_1,y_1)$ and $(x_2,y_2)$ is : $(y-y_1)=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$
Points (1, 3) and (3, 5)
=> Equation : $(y-3)=\frac{5-3}{3-1}(x-1)$
=> $y-3=x-1$
=> $y=x-1+3$
=> $y=x+2$
Comparing with equation $y=mx+c$, $m$ is the slope and $c$ is the y-intercept.
$\therefore$ y-intercept of the line joining two points (1, 3) and (3, 5) = 2
=> Ans – (C)
27) Answer (C)
Equation of line = $8x+4y=40$
=> $\frac{8x}{40}+\frac{4y}{40}=1$
=> $\frac{x}{5}+\frac{y}{10}=1$
Thus, total length intercepted = $5+10=15$
=> Ans – (C)
28) Answer (D)
Equation : $7x+12y=16$
Solving the equation by putting $x=0$, => $12y=16$
=> $y=\frac{16}{12}=\frac{4}{3}$
Also, putting $y=0$, => $7x=16$
=> $x=\frac{16}{7}$
$\therefore$ Plotting the graph for points $(0,\frac{4}{3})$ and $(\frac{16}{7},0)$
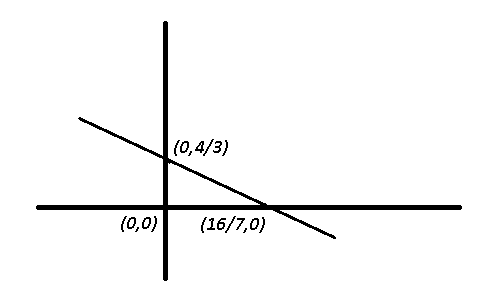
Thus, the equation $7x+12y=16$ passes through I, II and IV quadrants.
=> Ans – (D)
29) Answer (A)
Let the fraction be $x$
According to ques,
=> $x+\frac{1}{x}=\frac{113}{56}$
=> $\frac{x^2+1}{x}=\frac{113}{56}$
=> $56x^2-113x+56=0$
=> $56x^2-49x-64x+56=0$
=> $7x(8x-7)-8(8x-7)=0$
=> $(7x-8)(8x-7)=0$
=> $x=\frac{8}{7},\frac{7}{8}$
=> Ans – (A)
30) Answer (D)
Let total work to be done = L.C.M. (21,28) = 84
Manish can complete the work in 21 days, => Manish’s efficiency = $\frac{84}{21}=4$ units/day
Similarly, Karan’s efficiency = $\frac{84}{28}=3$ units/day
Now, (Manish+Karan)’s 7 day’s work = $(4+3)7=49$ units
Fraction of work that is left = $\frac{(84-49)}{84}=\frac{35}{84}=\frac{5}{12}$
=> Ans – (D)
31) Answer (A)
Slope of line having equation $ax+by+c=0$ is $\frac{-a}{b}$
Slope of line $-6x+4y+9=0$ is $\frac{-(-6)}{4}=\frac{3}{2}$
Product of slopes of two perpendicular lines = -1
=> Slope of other line which is perpendicular to it = $\frac{-2}{3}$
=> Ans – (A)
32) Answer (C)
$\frac{3}{4}=0.75$
$\frac{5}{12}=0.42$
$\frac{13}{16}=0.81$
$\frac{16}{29}=0.55$
$\frac{3}{8}=0.37$
Descending order = $\frac{13}{16}>\frac{3}{4}>\frac{16}{29}>\frac{5}{12}>\frac{3}{8}$
=> Ans – (C)
33) Answer (D)
Expression : $\frac{2x+y}{x+4y}=3$
=> $2x+y=3x+12y$
=> $3x-2x=y-12y$
=> $x=-11y$
$\therefore$ $\frac{x+y}{x+2y}$
= $\frac{-11y+y}{-11y+2y}$
= $\frac{-10y}{-9y}=\frac{10}{9}$
=> Ans – (D)
34) Answer (A)
Given : $(x+1)$ is a factor of $x^2 -7qx+12q=0$
=> $x=-1$ is a solution of above equation.
=> $(-1)^2-7q(-1)+12q=0$
=> $1+7q+12q=0$
=> $19q=-1$
=> $q=\frac{-1}{19}$
=> Ans – (A)
35) Answer (B)
Let the number be $x$
According to ques,
=> $(\frac{9}{15}\times\frac{7}{3}x)-(\frac{7}{12}\times\frac{3}{5}x)=7$
=> $(\frac{7x}{5})-(\frac{7x}{20})=7$
=> $\frac{x}{5}-\frac{x}{20}=1$
=> $\frac{4x-x}{20}=1$
=> $x=\frac{20}{3}=6.67$
=> Ans – (B)
36) Answer (C)
Let candies with Kirti = $x$ and with Divya = $(x+10)$
Total candies = $x+x+10=46$
=> $2x=46-10=36$
=> $x=\frac{36}{2}=18$
$\therefore$ Number of candies that Divya has = $18+10=28$
=> Ans – (C)
37) Answer (C)
Expression : $\frac{-5x}{3}+2=x-6$
=> $x+\frac{5x}{3}=2+6$
=> $\frac{3x+5x}{3}=8$
=> $8x=8\times3=24$
=> $x=\frac{24}{8}=3$
=> Ans – (C)
38) Answer (B)
Let the fraction be $x$
According to ques,
=> $x+\frac{1}{x}=\frac{61}{30}$
=> $\frac{x^2+1}{x}=\frac{61}{30}$
=> $30x^2-61x+30=0$
=> $30x^2-36x-25x+30=0$
=> $6x(5x-6)-5(5x-6)=0$
=> $(6x-5)(5x-6)=0$
=> $x=\frac{5}{6},\frac{6}{5}$
=> Ans – (B)
39) Answer (D)
Given = $Y:X:Z=4:5:6$
Let $X=5$, $Y=4$ and $Z=6$
To find : $\frac{X-Y+Z}{X+Y-Z}$
= $\frac{5-4+6}{5+4-6}=\frac{7}{3}$
=> Ans – (D)
40) Answer (B)
Expression : $X+\frac{4}{X}=4$
=> $\frac{x^2+4}{x}=4$
=> $x^2-4x+4=0$
=> $(x-2)^2=0$
=> $x-2=0$
=> $x=2$
$\therefore$ $X^6+1$ = $(2)^6+1$
= $64+1=65$
=> Ans – (B)





