Data Interpretation Questions For TISSNET
Download TISSNET Data Interpretation Questions and Answers PDF covering the important questions. Most expected questions with explanations for TISSNET 2021 exam.
Download DI Questions For TISSNET PDF
Download TISSNET Previous Papers PDF
Instructions
XYZ organization got into the business of delivering groceries to home at the beginning of the last month. They have a two-day delivery promise. However, their deliveries are unreliable. An order booked on a particular day may be delivered the next day or the day after. If the order is not delivered at the end of two days, then the order is declared as lost at the end of the second day. XYZ then does not deliver the order, but informs the customer, marks the order as lost, returns the payment and pays a penalty for non-delivery. The following table provides details about the operations of XYZ for a week of the last month. The first column gives the date, the second gives the cumulative number of orders that were booked up to and including that day. The third column represents the number of orders delivered on that day. The last column gives the cumulative number of orders that were lost up to and including that day. It is known that the numbers of orders that were booked on the 11th, 12th, and 13th of the last month that took two days to deliver were 4, 6, and 8 respectively
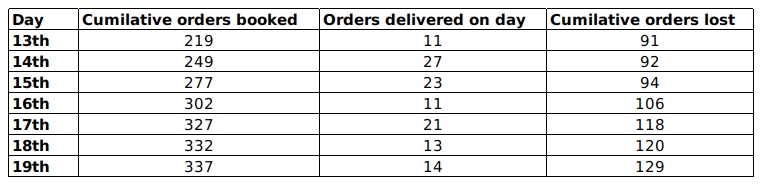
Question 1: On which of the following days was the number of orders booked the highest?
a) 12th
b) 15th
c) 13th
d) 14th
Question 2: The delivery ratio for a given day is defined as the ratio of the number of orders booked on that day which are delivered on the next day to the number of orders booked on that day which are delivered on the second day after booking. On which of the following days, was the delivery ratio the highest?
a) 15th
b) 16th
c) 13th
d) 14th
Question 3: On which of the following days was the number of orders booked the highest?
a) 12th
b) 15th
c) 13th
d) 14th
Question 4: Among the following days, the largest fraction of orders booked on which day was lost?
a) 15th
b) 16th
c) 13th
d) 14th
Download TISSNET Previous Papers PDF
Instructions
In a certain board examination, students were to appear for examination in five subjects:
English, Hindi, Mathematics, Science and Social Science. Due to a certain emergency situation, a few of the examinations could not be conducted for some students. Hence, some students missed one examination and some others missed two examinations. Nobody missed more than two examinations.
The board adopted the following policy for awarding marks to students. If a student appeared in all five examinations, then the marks awarded in each of the examinations were on the basis of the scores obtained by them in those examinations.
If a student missed only one examination, then the marks awarded in that examination was the average of the best three among the four scores in the examinations they appeared for. If a student missed two examinations, then the marks awarded in each of these examinations was the average of the best two among the three scores in the examinations they appeared for. The marks obtained by six students in the examination are given in the table below. Each of them missed either one or two examinations.
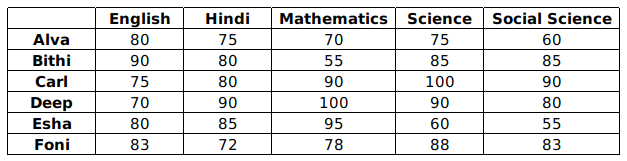
The following facts are also known.
I. Four of these students appeared in each of the English, Hindi, Science, and Social Science examinations.
II. The student who missed the Mathematics examination did not miss any other examination.
III. One of the students who missed the Hindi examination did not miss any other examination. The other student who missed the Hindi examination also missed the Science examination.
Question 5: For how many students can we be definite about which examinations they missed?
Question 6: For how many students can we be definite about which examinations they missed?
Question 7: What BEST can be concluded about the students who missed the Science examination?
a) Bithi and one out of Alva and Deep
b) Alva and Bithi
c) Deep and Bithi
d) Alva and Deep
Question 8: What BEST can be concluded about the students who missed the Science examination?
a) Bithi and one out of Alva and Deep
b) Alva and Bithi
c) Deep and Bithi
d) Alva and Deep
Question 9: Which students did not appear for the English examination?
a) Carl and Deep
b) Cannot be determined
c) Alva and Bithi
d) Esha and Foni
Question 10: Who among the following did not appear for the Mathematics examination?
a) Alva
b) Carl
c) Foni
d) Esha
Question 11: Who among the following did not appear for the Mathematics examination?
a) Alva
b) Carl
c) Foni
d) Esha
Take CMAT Free Mock Test With Solutions
Enroll to MAH MBA CET Crash Course
Instructions
Answer the questions with the given information and the data.
The following table gives number of T-Shirts sold (in thousand units) in Delhi and Mumbai. The T-Shirts are sold in different styles (S1, S2, S3, and S4) with different colours as shown in the table.
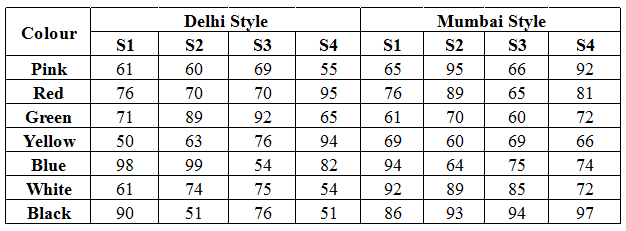
Question 12: Which style T-Shirt has highest difference in numberof units sold between twocities of Delhi and Mumbai?
a) S1
b) S2
c) S3
d) S4
Question 13: The average sales of which colour T-Shirt sold is same in both the cities ?
a) Yellow
b) Blue
c) Black
d) Red
Instructions
After receiving the disturbing news of falling standards the Supreme Council of Confederation of five Kingdoms is considering to conduct joint entrance examination for all student in these kingdoms for Vaidya Ratna course. As a first step, it has been decided to review the past five years data about the individual entrance examination of the kingdoms so that an appropriate action can be taken. Study the table given below and answer the questions.

Question 14: Highest number of candidates passed are from which of the following kingdoms for all the years together?
a) Anga
b) Banga
c) Gandhar
d) Dwarka
Question 15: What is the overall pass percentage of all the kingdoms in the year 2013?
a) 13.88
b) 14.88
c) 15.88
d) 16.88
Question 16: What is the overall pass percentage of all the kingdoms in the year 2013?
a) 13.88
b) 14.88
c) 15.88
d) 16.88
Question 17: What is the overall pass percentage of all the kingdoms in the year 2013?
a) 13.88
b) 14.88
c) 15.88
d) 16.88
Question 18: What is the overall pass percentage from Anga Kingdom for all the years together?
a) 16.7
b) 17.5
c) 18.7
d) 15.5
Download TISSNET Previous Papers PDF
Instructions
Read the following information on ‘Sectoral Trends in Mergers & Acquisitions in India (2001-02 to 2006-07)’ given in Tables below and answer the questions.
Table: Sector wise Number of ‘Mergers & Acquisitions’

Table: Sector wise Number of ‘Mergers’

Question 19: In which year maximum sectors have exhibited higher number of acquisitions compared to previous year?
a) 2003 – 04
b) 2004 – 05
c) 2005 – 06
d) 2006 – 07
Question 20: In which year maximum sectors have exhibited higher number of acquisitions compared to previous year?
a) 2003 – 04
b) 2004 – 05
c) 2005 – 06
d) 2006 – 07
Free MBA Preparation YouTube Videos
Join 7K MBA Aspirants Telegram Group
Answers & Solutions:
1) Answer (C)
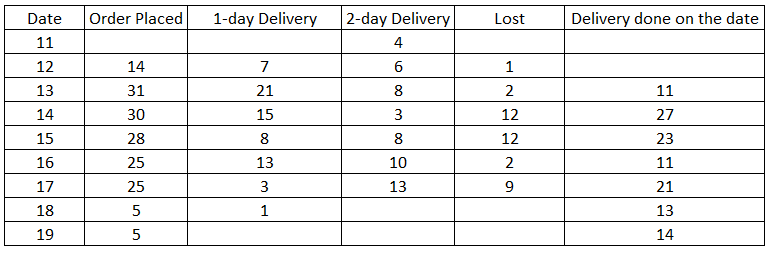
The cumulative orders booked by 19th are 337 and that of 18th are 332=> No. orders booked on 19th are 5
Similarly we can find the orders booked on that day till 14th.
Number of orders lost that were booked on 12th = Cumulative orders lost till 14th-Cumulative orders lost till 13th =92-91=1
Similarly, the number of orders lost till 17th can be found out.
Number
of orders delivered on 13th are 11 out of which 4 are orders which were
booked in 11th so, 7 must be the orders which were booked on 12th.
Similarly, we can find the orders which took 1day and 2 days to get delivered till 17th.
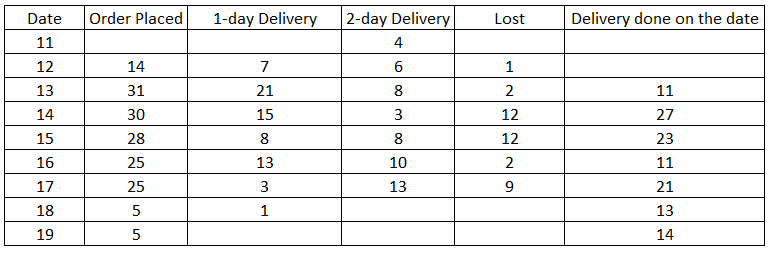
Now, total number of orders booked on 12th will be 7+6+1=14.
The total number of orders placed on 13th = 21+8+2 = 31
FRom the table we can determine that among options, number of orders booked on 13th are maximum.
2) Answer (D)
The cumulative orders booked by 19th are 337 and that of 18th are 332=> No. orders booked on 19th are 5
Similarly we can find the orders booked on that day till 14th.
Number of orders lost that were booked on 12th = Cumulative orders lost till 14th-Cumulative orders lost till 13th =92-91=1
Similarly, the number of orders lost till 17th can be found out.
Number
of orders delivered on 13th are 11 out of which 4 are orders which were
booked in 11th so, 7 must be the orders which were booked on 12th.
Similarly, we can find the orders which took 1day and 2 days to get delivered till 17th.
Now, total number of orders booked on 12th will be 7+6+1=14.
From the table we can determine that among options, number of orders booked on 13th are maximum.
For 15 the delivery ratio = 8/8 = 1
For 16 the delivery ratio = 13/10 = 1.3
For 13 the delivery ratio = 21/8 = 2.625
For 14 the delivery ratio = 15/3 = 5
Hence Option D
3) Answer (C)
The cumulative orders booked by 19th are 337 and that of 18th are 332=> No. orders booked on 19th are 5
Similarly we can find the orders booked on that day till 14th.
Number of orders lost that were booked on 12th = Cumulative orders lost till 14th-Cumulative orders lost till 13th =92-91=1
Similarly, the number of orders lost till 17th can be found out.
Number
of orders delivered on 13th are 11 out of which 4 are orders which were
booked in 11th so, 7 must be the orders which were booked on 12th.
Similarly, we can find the orders which took 1day and 2 days to get delivered till 17th.

Now, total number of orders booked on 12th will be 7+6+1=14.
The total number of orders placed on 13th = 21+8+2 = 31
FRom the table we can determine that among options, number of orders booked on 13th are maximum.
Get 5 CMAT Mocks for just Rs. 299
Download CMAT Previous Papers Andriod App
4) Answer (A)
The cumulative orders booked by 19th are 337 and that of 18th are 332=> No. orders booked on 19th are 5
Similarly we can find the orders booked on that day till 14th.
Number of orders lost that were booked on 12th = Cumulative orders lost till 14th-Cumulative orders lost till 13th =92-91=1
Similarly, the number of orders lost till 17th can be found out.
Number of orders delivered on 13th are 11 out of which 4 are orders which were booked in 11th so, 7 must be the orders which were booked on 12th.
Similarly, we can find the orders which took 1day and 2 days to get delivered till 17th.
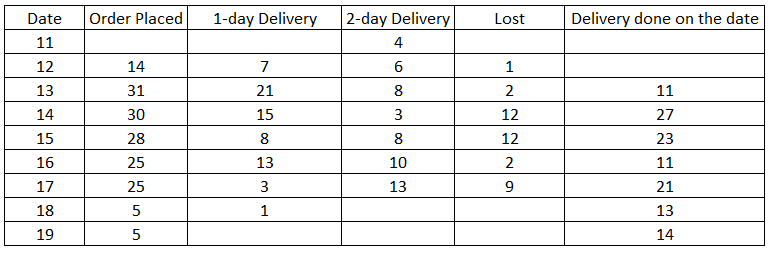
Now, total number of orders booked on 12th will be 7+6=1=14.
Fraction of orders booked on 15th that were lost = 12/28
Fraction of orders booked on 16th that were lost = 2/25
Fraction of orders booked on 13th that were lost =2/31
Fraction of orders booked on 14th that were lost = 8/30.
.’. Option A is correct answer.
5) Answer: 4
Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.
For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)
Avg. = 270/3 = 90 which matches the given value
$\therefore\ $ Carl missed his Mathematics examination.
Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.
Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.
For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)
Avg. = 240/3 = 80 which matches the given value
$\therefore\ $ Esha most likely missed her English examination.
For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)
Avg. = 249/3 = 83 which matches the given value
$\therefore\ $ Foni most likely missed her English examination.
Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.
For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.
We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.
For Bithi: Best 2 out 3 – 90(English), 80(Hindi)
Avg = 170/2 = 85 which matches the given value
$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.
We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.
Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).
Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):
Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi
Except for Alva and Deep, we can conclusively comment of the missed subjects of the rest four. Hence, the correct answer is 4.
6) Answer: 4
Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.
For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)
Avg. = 270/3 = 90 which matches the given value
$\therefore\ $ Carl missed his Mathematics examination.
Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.
Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.
For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)
Avg. = 240/3 = 80 which matches the given value
$\therefore\ $ Esha most likely missed her English examination.
For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)
Avg. = 249/3 = 83 which matches the given value
$\therefore\ $ Foni most likely missed her English examination.
Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.
For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.
We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.
For Bithi: Best 2 out 3 – 90(English), 80(Hindi)
Avg = 170/2 = 85 which matches the given value
$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.
We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.
Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).
Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):
Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi
Except for Alva and Deep, we can conclusively comment of the missed subjects of the rest four. Hence, the correct answer is 4.
7) Answer (A)
Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.
For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)
Avg. = 270/3 = 90 which matches the given value
$\therefore\ $ Carl missed his Mathematics examination.
Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.
Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.
For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)
Avg. = 240/3 = 80 which matches the given value
$\therefore\ $ Esha most likely missed her English examination.
For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)
Avg. = 249/3 = 83 which matches the given value
$\therefore\ $ Foni most likely missed her English examination.
Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.
For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.
We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.
For Bithi: Best 2 out 3 – 90(English), 80(Hindi)
Avg = 170/2 = 85 which matches the given value
$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.
We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.
Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).
Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):
Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi
Hence, the correct answer to this question is Option A: Bithi & one out of Alva and Deep.
8) Answer (A)
Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.
For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)
Avg. = 270/3 = 90 which matches the given value
$\therefore\ $ Carl missed his Mathematics examination.
Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.
Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.
For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)
Avg. = 240/3 = 80 which matches the given value
$\therefore\ $ Esha most likely missed her English examination.
For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)
Avg. = 249/3 = 83 which matches the given value
$\therefore\ $ Foni most likely missed her English examination.
Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.
For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.
We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.
For Bithi: Best 2 out 3 – 90(English), 80(Hindi)
Avg = 170/2 = 85 which matches the given value
$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.
We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.
Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).
Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):
Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi
Hence, the correct answer to this question is Option A: Bithi & one out of Alva and Deep.
9) Answer (D)
Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores. After estimating the average scores for the rest of the candidates, we observe that only Carl has missed his Mathematics examination.
For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)
Avg. = 270/3 = 90 which matches the given value
$\therefore\ $ Carl missed his Mathematics examination.
Further, based on Condition III, we can surmise that the student who missed Hindi and Science should have similar average scores in these two subjects. We notice that Alva has the same score of 75 in both Hindi and Science. The same can be said about Deep, who has a score of 90 in both these subjects. Thus, one out of Alva and Deep missed out on Hindi and Science examination, while the second individual missed out only on the Hindi examination.
Since we know that Carl, Alva and Deep are unlikely to have missed out on the English exam, we can divert our attention to determining which individual out of Bithi, Esha and Foni failed to appear for this subject. However, we notice that Bithi’s English score is greater than the rest of her scores, thereby helping us eliminate her as the potential candidate.
For Esha: best 3 out of 4 – 85(Hindi), 95(Mathematics), 60(Science)
Avg. = 240/3 = 80 which matches the given value
$\therefore\ $ Esha most likely missed her English examination.
For Foni: best 3 out of 4 – 78(Mathematics), 83(Social Science), 88(Science)
Avg. = 249/3 = 83 which matches the given value
$\therefore\ $ Foni most likely missed her English examination.
Based on Condition I, we know that exactly two candidates missed the examinations for English, Hindi, Science, and Social Science.
For English, we determined these individuals to be Esha and Foni. For Hindi, we determined these individuals to be Alva and Deep. For Science, we know one of the individuals is either Alva or Deep. Given that Carl, Alva and Deep cannot be a part of the group that missed Science or Social Science exam, we can proceed by carefully scrutinizing the rest of the group that includes Bithi, Esha and Foni.
We notice that Bithi has a similar score in both Science and Social Science examination. Assuming that she did miss these exams, let us proceed to check if this was actually the case.
For Bithi: Best 2 out 3 – 90(English), 80(Hindi)
Avg = 170/2 = 85 which matches the given value
$\therefore\ $ Bithi is likely to have missed her Science and Social Science examinations.
We additionally notice that Foni has a similar score in English and Social Science. On considering the best 2 out of 3 scores, the average value of the score for both the subject holds (equal to 83). Thus, we can conclude that Bithi and Foni missed their Social Science examination.
Thus, the students who missed just one exam were: Carl (Mathematics); Esha (English) and one out of Alva and Deep (Hindi).
Hence of the six students, we can correctly determine the missed subjects for four of them (except Alva and Deep):
Mathematics: Carl ; English: Esha & Foni ; Hindi: Alva & Deep; Science: Bithi & one out of Alva and Deep ; Social Science: Foni & Bithi
Hence, the correct answer to this question is Option D: Esha and Foni.
10) Answer (B)
Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores.
For Alva: best 3 out of 4 – 80(English), 75(Hindi), 75(Science)
Avg. = 230/3 = 76.67 $\ne\ $ 70
For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)
Avg. = 270/3 = 90 which matches the given value
$\therefore\ $ Carl most likely missed his Mathematics examination.
For Foni: best 3 out of 4 – 83(English), 83(Social Science), 88(Science)
Avg. = 254/3 = 84.67 $\ne\ $ 78
Hence, we observe that only Carl has missed his Mathematics examination. Hence, Option B is the correct answer.
11) Answer (B)
Based on Condition II, we understand that the student who missed the Mathematics examination did not miss any other examination. This indicates that the Maths score is bound to be the average of the best 3 out of the 4 exam scores obtained by this candidate. Based on this inference, we can proceed with identifying the math score that can be represented as an average of the rest of the scores. We can straightaway eliminate Deep and Esha as potential candidates, given that their Mathematics score is greater than the rest of the exam scores.
For Alva: best 3 out of 4 – 80(English), 75(Hindi), 75(Science)
Avg. = 230/3 = 76.67 $\ne\ $ 70
For Carl: best 3 out of 4 – 80(Hindi), 90(Social Science), 100(Science)
Avg. = 270/3 = 90 which matches the given value
$\therefore\ $ Carl most likely missed his Mathematics examination.
For Foni: best 3 out of 4 – 83(English), 83(Social Science), 88(Science)
Avg. = 254/3 = 84.67 $\ne\ $ 78
Hence, we observe that only Carl has missed his Mathematics examination. Hence, Option B is the correct answer.
Download TISSNET Previous Papers PDF
12) Answer (D)
S1- Delhi = 507 ; S1- Mumbai = 543 ; Difference = 36
S2-Delhi = 506 ; S2 – Mumbai=560 ; Difference = 54
S3 – Delhi =515 ; S3 – Mumbai = 154 ; Difference = 1
S4 – Delhi = 496 ; S4 – Mumbai = 554 ; Difference = 58.
Option D, S4 is the correct answer.
13) Answer (D)
Yellow – Delhi : 70.75 ; Yellow – Mumbai : 66.
Blue – Delhi : 83.25 ; Blue – Mumbai :76.75
Black – Delhi :67 ; Black – Mumbai :92.5
Red – Delhi :77.75 ; Red – Mumbai :77.75.
Red has same average sales in both cities
14) Answer (D)
Total no of candidates passed from Anga Kingdoms for all years = 850+770+1200+750+1190 = 4760
Total no of candidates passed from Banga Kingdoms for all years = 640+810+1235+880+660 = 4225
Total no of candidates passed from Gandhar Kingdoms for all years = 765+595+810+520+1200 = 3890
Total no of candidates passed from Dwarka Kingdoms for all years = 780+1120+715+935+1330 = 4880
Hence, Dwarka is the kingdom with highest number of candidates passed.
15) Answer (B)
Total no of students passed in 2013 = 770+810+275+1120+595 = 3570
Total no of students appeared in 2013 = 5500+4500+2500+8000+3500 = 24000
Overall pass percentage of all kingdoms in 2013 = (Total no of students passed in 2013 / Total no of students appeared in 2013) *100
= (3570/24000)*100
= 14.875 = 14.88 (Rounded off)
16) Answer (B)
Total no of students passed in 2013 = 770+810+275+1120+595 = 3570
Total no of students appeared in 2013 = 5500+4500+2500+8000+3500 = 24000
Overall pass percentage of all kingdoms in 2013 = (Total no of students passed in 2013 / Total no of students appeared in 2013) *100
= (3570/24000)*100
= 14.875 = 14.88 (Rounded off)
17) Answer (B)
Total no of students passed in 2013 = 770+810+275+1120+595 = 3570
Total no of students appeared in 2013 = 5500+4500+2500+8000+3500 = 24000
Overall pass percentage of all kingdoms in 2013 = (Total no of students passed in 2013 / Total no of students appeared in 2013) *100
= (3570/24000)*100
= 14.875 = 14.88 (Rounded off)
18) Answer (A)
Pass Percentage = ( No of students who passed the examination / No of students who appeared for the examination)*100
=(850+770+1200+750+1190/5000+5500+6000+5000+7000)*100
=(4760/28500)*100
=16.7
19) Answer (C)
20) Answer (C)




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
