Coordinate GeometryQuestions For SSC GD PDF
SSC GD Constable Coordinate Geometry Question paper with answers download PDF based on SSC GD exam previous papers. 40 Very important Coordinate Geometry questions for GD Constable.
DOWNLOAD COORDINATE GEOMETRY QUESTIONS FOR SSC GD PDF
GET 20 SSC GD MOCK FOR JUST RS. 117
Download SSC GD Important Questions PDF
1500+ Must Solve Questions for SSC Exams (Question bank)
Question 1: What is the equation of a line which passes through the point of intersection of lines A:x-3y=7 and B:2x+y=-7 and the required line is also perpendicular to line x+4y=10 ?
a) 4x-y+4=0
b) 4x-y+5=0
c) 4x-3y-1=0
d) x-4y-10=0
Question 2: Equation of one of the diagonals of a rhombus is 2x+3y=10. what is the equation of the other diagonal passing through the point (1,3) ?
a) $3x+2y-9=0$
b) $6x-4y+5=0$
c) $3x-2y+3=0$
d) $2x+3y-11=0$
Question 3: The straight line y=3x must pass through the point:
a) (0,1)
b) (0,0)
c) (2,0)
d) (1,2)
Question 4: A is a point on the x-axis with abscissa – 8 and B is the pint on the y-axis with ordinate 15. The length of AB is
a) 19 units
b) 21 units
c) 17 units
d) 23 units
Question 5: What is the reflection of the point (-5, -2) in the line y = 1?
a) (-5, 1)
b) (-5, 4)
c) (-5, 0)
d) (-5, 5)
Download SSC GD FREE PREVIOUS PAPERS
Question 6: If (1, 3) is the centroid of triangle ABC, with co-ordinates A(1, 6), B(3 , a) & C(b, 1), what is the value of a + b?
a) 5
b) 1
c) 6
d) 4
Question 7: What is the reflection of the point ( 6, -3) about the line y = -3?
a) (6, 3)
b) (6, 0)
c) (6, -6)
d) (6, -3)
Question 8: Find the area (in sq units) enclosed by y = 0, x+6=0 and 2x-3y=6.
a) 9
b) 16
c) 20
d) 27
Question 9: What is the area of the triangle made by line 3x+4y = 24 with the coordinate axes?
a) 6 square units
b) 12 square units
c) 24 square units
d) 48 square units
Question 10: A cube is cut into 8 equal smaller cubes.The percentage change in the surface area is
a) 80%
b) 50%
c) 150%
d) 100%
DOWNLOAD APP TO ACESS DIRECTLY ON MOBILE
Question 11: Find the centroid of the triangle formed by the vertices, P(-4,-2) Q(-3, -5) and R(1, 1) ?
a) (2, -2)
b) (-2, 2)
c) (-2,-2)
d) (2, 2)
Question 12: Which of the following represents hyperbola ?
a) $x^2+y^2 = a^2$
b) $\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$
c) $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$
d) None of the above
Question 13: Find the area of triangle formed by the line 6x+7y = 21 with coordinate axes ?
a) 5.25 sq.units
b) 6.25 sq.units
c) 9.25 sq.units
d) 12.25 sq.units
Question 14: What is the reflection of the point ( -2, -3) in the line y = -4?
a) (-2, -2)
b) (-2, -5)
c) (1, -2)
d) (2, 5)
Question 15: What is the equation of a circle of radius 1 unit centered at (-5, -4) ?
a) $x^2+y^2+10x+8y+40 = 0$
b) $x^2+y^2-10x+8y+40 = 0$
c) $x^2+y^2+10x-8y+40 = 0$
d) $x^2+y^2+10x+8y-40 = 0$
Download SSC GD Constable Syllabus PDF
Question 16: If the ordinate and abscissa of (2k+3, 4+k) are equal, then find the value of k ?
a) 0
b) 1
c) 2
d) 3
Question 17: The coordinates of the vertices of a right angled triangle are A(4,3), B(8,-2) and C(4, -2). It is known that the triangle is right angled at C. Find the orthocenter of the triangle ABC ?
a) (4,-2)
b) (8,3)
c) (6,3)
d) (2,3)
Question 18: What is the reflection of the point ( -4, -4) in the line x = 1 ?
a) (-6, 4)
b) (-6, -4)
c) (6, 4)
d) (6, -4)
Question 19: Which of the following represents Ellipse ?
a) $x^2-y^2 = a^2$
b) $\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$
c) $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$
d) None of the above
Question 20: Find the centroid of the triangle formed by the vertices, P(2,3) Q(-3, -5) and R(1, -4) ?
a) (-1, 2)
b) (0, 2)
c) (1,-2)
d) (0, -2)
Question 21: Find the area of triangle formed by the line 3x+5y = 15 with coordinate axes ?
a) 3.5 sq.units
b) 5.5 sq.units
c) 7.5 sq.units
d) 9.5 sq.units
Question 22: What is the reflection of the point ( -3, -2) in the line y = 0?
a) (-3, 2)
b) (3, 2)
c) (3, -2)
d) (-3, -2)
Question 23: If the ordinate and abscissa of (k+1, 1-k) are equal, then find the value of k ?
a) 0
b) 1
c) 2
d) 3
Question 24: What is the equation of a circle of radius 5 units centered at (-4, 2) ?
a) $x^2+y^2-2x-4y+5=0$
b) $x^2+y^2+8x-4y+5 = 0$
c) $x^2+y^2-8x-4y-5 = 0$
d) $x^2+y^2+8x-4y-5 = 0$
Question 25: The coordinates of the vertices of a right angled triangle are A(8,-2) B(8,3) and C(2, 3). It is known that the triangle is right angled at B. Find the orthocenter of the triangle ABC ?
a) (2,-2)
b) (8,3)
c) (6,3)
d) (2,3)
Question 26: What is the reflection of the point ( -2, -2) in the line x = 2?
a) (-6, -2)
b) (6, -2)
c) (-6, 2)
d) (6, 2)
100+ Free GK Tests for SSC Exams
Question 27: Find the distance between the points P(2,4) and Q(-2,1) ?
a) 4 units
b) 5 units
c) 6
d) 7 units
Question 28: A right angled triangle A(2,3), B(8,3) and C(2, -1) is right angled at A. What is the orthocentre of triangle ABC ?
a) (10,2)
b) (5,2)
c) (5,1)
d) (2,3)
Question 29: Find the area of triangle formed by the line 2x+3y = 6 with coordinate axes ?
a) 3 sq.units
b) 6 sq.units
c) 9 sq.units
d) 12 sq.units
Question 30: What is the reflection of the point ( -1, 4) in the line y = -3?
a) (1, -10)
b) (-1, 10)
c) (-1, -10)
d) (1, 10)
Question 31: Find the slope of the line 3x-4y+4 = 0 ?
a) 4/3
b) 3/2
c) 2/3
d) 3/4
Question 32: What is the equation of a circle of radius 3 units centered at (-1, 3) ?
a) $x^2+y^2-2x-4y+5=0$
b) $x^2+y^2-2x-6y+1 = 0$
c) $x^2+y^2+2x-6y+1 = 0$
d) $x^2+y^2+2x-6y-1 = 0$
Question 33: If the ordinate and abscissa of (2k+3, 6-k) are equal, then find the value of k ?
a) 1
b) 2
c) 3
d) 4
Question 34: What is the reflection of the point ( -3, -2) in the line x = -1?
a) (-1, -2)
b) (-1, 2)
c) (1, -2)
d) (1, 2)
Question 35: The coordinates of the vertices of a right angled triangle are A(6,-7) B(8,3) and C(6, 3), which is right angled at C. Find the orthocenter of the triangle ABC ?
a) (2,-2)
b) (8,3)
c) (6,3)
d) (2,3)
Question 36: Find the value of k (greater than 0) for which the lines (2k-1)x+3y-2 = 0 and 3x+(4k-5)y+4 = 0 are parallel ?
a) 1
b) 2
c) 3
d) 4
Question 37: Find the area of a right angled triangle formed by the vertices A(6,-7) B(8,3) and C(6, 3), which is right angled at C ?
a) 25 sq.units
b) 20 sq.units
c) 15 sq.units
d) 10 sq.units
Question 38: Find the area of triangle formed by the line 4x+3y = 12 with coordinate axes ?
a) 3 sq.units
b) 6 sq.units
c) 9 sq.units
d) 12 sq.units
Question 39: What is the reflection of the point ( -2, 2) in the line y = -2?
a) (-2, -6)
b) (2, -6)
c) (6, -2)
d) (6, 2)
Question 40: If the ordinate and abscissa of (2k, 6-k) are equal, then find the value of k ?
a) 1
b) 2
c) 3
d) 4
Answers & Solutions:
1) Answer (B)
The point of intersection of the lines A and B is (-2,-3)
the line is perpendicular to x+4y=10
Slope of x+4y=10 is ($\frac{-1}{4}$)
$\frac{-1}{4}\times s $=-1
s=4
Equation of line is 4(x+2)=y+3
4x+8=y+3
4x-y+5=0
2) Answer (C)
Diagonals of a rhombus are perpendicular to each other.
Lines perpendicular to each other have the product of their slopes = -1
Slope of the line 2x+3y-10=0 is $-(\frac{a}{b})$
Slope = $\frac{-2}{3}$
Then slope of the other line is $ \frac{3}{2}$.
$\therefore$ required equation is $\frac{3}{2}(x-1)=(y-3)$
$3x-3=2y-6$
$ 3x-2y+3=0$
3) Answer (B)
Equation of line = $y=3x$
(A) : (0,1)
=> L.H.S. = $1\neq$ R.H.S. = $3(0)=0$
(B) : (0,0)
=> L.H.S. = $0=$ R.H.S. = $3(0)=0$
=> Ans – (B)
4) Answer (C)

Now, OA = 8 units and OB = 15 units
=> $(AB)^2=(OA)^2+(OB)^2$
=> $(AB)^2=(8)^2+(15)^2$
=> $(AB)^2=64+225=289$
=> $AB=\sqrt{289}=17$ units
=> Ans – (C)
5) Answer (B)
We can see that (-5, -2) is 3 units away from y = 1
X coordinate of the point will remain unchanged while y axis will change
$\Rightarrow$ $1 = \frac{-2 + b}{2}$
$\Rightarrow$ $2 = -2 + b$
$\Rightarrow$ $b = 4$
Alternatively from graph we can see the reflection of point as well. (Answer :B)

6) Answer (B)
Centroid = $(\frac{x_{1}+x_{2}+x_{3}}{3} , \frac{y_{1}+y_{2}+y_{3}}{3})$
$(1, 3)$ = $(\frac{1 + 3 + b}{3} , \frac{6 + a + 1}{3})$
$\Rightarrow$ $1 = \frac{1 + 3 + b}{3}$
$\Rightarrow$ $b + 4 = 3$
$\Rightarrow$ $b = -1$
Also, we know that $3 = \frac{6 + a + 1}{3}$
$\Rightarrow$ $a + 7 = 9$
$\Rightarrow$ $a = 2$
Therefore, a+b = 2 -1 = 1.
Hence, option B is the right answer.
7) Answer (D)
Since the given point (6, -3) lies on the line y = -3 itself, the point and its reflection will coincide.
Therefore, the reflection of point = (6, -3).
Hence, option D is the right answer.
8) Answer (D)
9) Answer (C)
The given line will cut the x-axis at a point where the y co-ordinate will be equal to zero.
$\Rightarrow$ 3x + 4*0 = 24.
$\Rightarrow$ x = 8.
So, the point of intersection on the x axis will be (8, 0).
Similarly, the line will cut y-axis at a point where the x co-ordinate will be equal to zero.
$\Rightarrow$ 3*0 + 4y = 24.
$\Rightarrow$ y = 6.
So, the point of interaction on the y axis will be (0, 6)

We can see that $\triangleOAB$ is right-angled at O.
So, the area of $\triangleOAB$ = $\frac{1}{2} * OA * OB$
= $\frac{1}{2} * 6 * 8$
= 24 sq units.
Therefore, option C is the right answer.
10) Answer (D)
Let us assume the side of the original cube to be 2a units.
=> The surface area of the bigger cube = $6*(2a)^{2} = 24(a)^{2}$
When we cut the original cube to get 8 smaller cubes, each side will become half of its original length.
So, the side of smaller cube will be 2a/2 = a units in length.
Surface area of 1 smaller cube = $6*(a)^{2} = 6(a)^{2}$
Total surface area of 8 cubes combined = $8 * 6(a)^{2} = 48(a)^{2}$
So, the percentage change in the surface area = $\frac{48(a)^{2} – 24(a)^{2}}{24(a)^{2}} \times 100$ = 100 %.
Therefore, option D is the right answer.
11) Answer (C)
Centroid = ($\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}$) = ($\frac{-4-3+1}{3}, \frac{-2-5+1}{3}$) = (-2, -2)
So the answer is option C.
12) Answer (C)
Option A & B, represent Ellipse. ($\because$ general form of Ellipse is $\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$)
Option C represents Hyperbola. ($\because$ general form of Hyperbola is $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$)
So the answer is option C.
13) Answer (A)
Area of the line $\frac{x}{a}+\frac{y}{b} = 1$, made by Coordinate axes is $\frac{1}{2}ab$.
$6x+7y = 21 ==> \frac{x}{3.5}+\frac{y}{3} = 1$
Area = $\frac{1}{2}ab = \frac{1}{2}(3.5)(3) = 5.25 sq.units$
So the answer is option A.
14) Answer (B)
(-2, -3) lies above the line y=-4
Distance b/w the line & point is -3-(-4) = 1
So its reflection must be 1 unit below the line , i.e; (-2, -4-1) = (-2, -5)
So the answer is option B.
15) Answer (A)
Eq.of a circle of radius r and having centre at ($x_1, y_1$) is $(x-x_1)^2+(y-y_1)^2=r^2$
Hence, $(x+5)^2+(y+4)^2=1^2$
==> $x^2+10x+25+y^2+8y+16 = 1$
==> $x^2+y^2+10x+8y+40 = 0$
So the answer is option A.
16) Answer (B)
2k+3 = 4+k
2k-k = 4-3
k = 1
So the answer is option B.
17) Answer (A)
Orthocentre of a right angled triangle is the vertex where the angle is 90°
Here, it is right angled at C, so C(4, -2) is the orthocentre.
So the answer is option A.
18) Answer (D)
(-4, -4) lies on left to the line x=1
Distance b/w the line & point is 1-(-4) = 5
So its reflection must be 5 units to the right side the line , i.e; (1+5, -4) = (6, -4)
So the answer is option D.
19) Answer (B)
Option A & C, represent hyperbola. ($\because$ general form of hyperbola is $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$)
Option B represents Ellipse. ($\because$ general form of Ellipse is $\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$)
So the answer is option B.
20) Answer (D)
Centroid = ($\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}$) = ($\frac{2-3+1}{3}, \frac{3-5-4}{3}$) = (0, -2)
So the answer is option D.
21) Answer (C)
Area of the line $\frac{x}{a}+\frac{y}{b} = 1$, made by Coordinate axes is $\frac{1}{2}ab$.
$3x+5y = 15 ==> \frac{x}{5}+\frac{y}{3} = 1$
Area = $\frac{1}{2}ab = \frac{1}{2}(3)(5) = 7.5 sq.units$
So the answer is option C.
22) Answer (A)
(-3, -2) lies below the line y=0
Distance between the line & point is 0-(-2) = 2
So its reflection must be 2 units above the line , i.e; (-3, 0+2) = (-3, 2)
So the answer is option A.
23) Answer (A)
k+1 = 1-k
2k = 0
k = 0
So the answer is option A.
24) Answer (D)
Eq.of a circle of radius r and having centre at ($x_1, y_1$) is $(x-x_1)^2+(y-y_1)^2=r^2$
Hence, $(x+4)^2+(y-2)^2=5^2$
==> $x^2+8x+16+y^2-4y+4 = 25$
==> $x^2+y^2+8x-4y-5 = 0$
So the answer is option D.
25) Answer (B)
Orthocentre of a right angled triangle is the vertex where the angle is 90°
Here, it is right angled at B, so B(8, 3) is the orthocentre.
So the answer is option B.
26) Answer (B)
(-2, -2) lies on left to the line x=2
Distance b/w the line & point is 2-(-2) = 4
So its reflection must be 4 units to the right side the line , i.e; (2+4, -2) = (6, -2)
So the answer is option B.
27) Answer (B)
Distance = $\sqrt{(y_2-y_1)^2+(x_2-x_1)^2} = \sqrt{(1-4)^2+(-2-2)^2} = \sqrt{9+16} = 5$
So the answer is option B.
28) Answer (D)
Orthocentre of a right angled triangle is the vertex where the angle is 90°
Here, it is right angled at A, so C(2, 3) is the Orthocentre.
So the answer is option D.
29) Answer (A)
Area of the line $\frac{x}{a}+\frac{y}{b} = 1$, made by Coordinate axes is $\frac{1}{2}ab$.
$2x+3y = 6 ==> \frac{x}{3}+\frac{y}{2} = 1$
Area = $\frac{1}{2}ab = \frac{1}{2}(3)(2) = 3 sq.units$
So the answer is option A.
30) Answer (C)
(-1,4) lies above the line y=-3
Distance b/w the line & point is 4-(-3) = 7
So its reflection must be 7 units below the line , i.e; (-1, -3-7) = (-1, -10)
So the answer is option C.
31) Answer (D)
Slope of the line ax+by+c = 0 is -a/b
Hence slope of the line 3x-4y+4 = 0 is -3/-4 = 3/4
So the answer is option D.
32) Answer (C)
Eq.of a circle of radius r and having centre at ($x_1, y_1$) is $(x-x_1)^2+(y-y_1)^2=r^2$
Hence, $(x+1)^2+(y-3)^2=3^2$
==> $x^2+2x+1+y^2-6y+9 = 9$
==> $x^2+y^2+2x-6y+1 = 0$
So the answer is option C.
33) Answer (A)
2k+3 = 6-k
2k+k = 6-3
3k = 3
k = 1
So the answer is option A.
34) Answer (C)
(-3, -2) lies on left to the line x=-1
Distance b/w the line & point is -1-(-3) = 2
So its reflection must be 2 units to the right side the line , i.e; (-1+2, -2) = (1, -2)
So the answer is option C.
35) Answer (C)
Orthocentre of a right angled triangle is the vertex where the angle is 90°
Here, it is right angled at C, so C(6, 3) is the orthocentre.
So the answer is option C.
36) Answer (B)
Slope of the line ax+by+c = 0 is -a/b
For parallel lines, slopes are equal
==>$\frac{-(2k-1)}{3} = \frac{-3}{4k-5}$
==>$8k^2-14k-4 = 0$
==>$4k^2-7k-2 = 0$
==>$(4k+1)(k-2) = 0$
==>$k = -1/4$ or $k = 2$
So the answer is option B.
37) Answer (D)
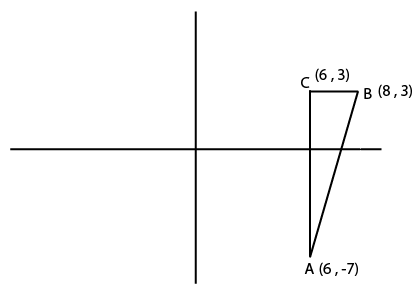
AC = 3-(-7) = 10
BC = 8-6 = 2
Area of given triangle = $\frac{1}{2}(AC)(BC) = \frac{1}{2}(10)(2) = 10 sq.cm$
So the answer is option D.
38) Answer (B)
Area of the line $\frac{x}{a}+\frac{y}{b} = 1$, made by Coordinate axes is $\frac{1}{2}ab$.
$4x+3y = 12 ==> \frac{x}{3}+\frac{y}{4} = 1$
Area = $\frac{1}{2}ab = \frac{1}{2}(3)(4) = 6 \text{ sq.units}$
So the answer is option B.
39) Answer (A)
(-2, 2) lies above the line y=-2
Distance between the line & point is 2-(-2) = 4
So its reflection must be 4 units below the line , i.e; (-2, -2-4) = (-2, -6)
So the answer is option A.
40) Answer (B)
2k = 6-k
3k = 6
k = 2
So the answer is option B.
Download SSC GD Previous Papers PDF
DOWNLOAD APP FOR SSC FREE MOCKS
We hope this Coordinate Geometry questions for SSC GD will be highly useful for your preparation.





