Clock Questions for SSC CGL PDF:
Download SSC CGL Clock questions with answers PDF based on previous papers very useful for SSC CGL exams. 25 Very important Clock objective questions for SSC exams.
Download Clock Questions for SSC CGL PDF
Question 1: If a clock started at noon, then the angle turned by hour hand at 3.45 PM is
a) 117 1°/2
b) 104 1°/2
c) 97 1°/2
d) 112 1°/2
Question 2: Find the angle between the minutes hand and the hours hand at 10:40 ?
a) 90°
b) 85°
c) 80°
d) 75°
Question 3: At what between 10 am and 11 am will the angle between the minutes hand and hours hand be 3° (assume that the hours hand is closer to 12 than than the minutes hand) ?
a) 10:52
b) 10:53
c) 10:54
d) 10:55
Question 4: At what time the hands of the clock show a mirror image of 4:10 ?
a) 7:10
b) 7:40
c) 7:50
d) 8:10
Question 5: A watch gains 6 minutes in one hour and was set right at 8 AM. What time will it show at 6PM on the same day?
a) 8pm
b) 7pm
c) 8:30pm
d) 7:30pm
SSC CGL Previous Papers Download PDF
Question 6: In how many ways can Alex and his 5 friends be seated around a circular table if clockwise and anti-clockwise directions are considered different?
a) 120
b) 720
c) 60
d) 360
e) None of the above
Question 7: In how many ways can 8 people be seated around a circular table (if clockwise direction is not the same as anti-clockwise direction)?
a) 8!*2
b) 8!/2
c) 8!
d) 7!/2
e) 7!
Question 8: There are 5 chairs arranged in a circular manner in a square room. Total 6 people are to meet in a room, but since only 5 chair are available 1 person will have to stand at one of the corners of the room. In how many ways this can be done? Also note that clockwise arrangement and anti-clockwise arrangement are different.
a) 642
b) 386
c) 482
d) 524
e) 576
Question 9: A, C are running with speeds of 20m/s, 24m/s on a circular track. A is running in the clockwise direction and C is running in the anti-clockwise direction. At how many distinct points they meet on that circular track?
a) 5
b) 6
c) 11
d) 10
e) a :None of these
Question 10: A and B are running in opposite directions around a circular track of length 120 meters. If the speeds of A and B are in the ratio 3:2, find the minimum distance between their first and 13th meeting points.
a) 36 m
b) 24 m
c) 12 m
d) 20 m
e) None of these
18000+ Questions – Free SSC Study Material
Question 11: What is the angle between the hour and minute hands of a clock 30 minutes after they meet for the third time in a day?
a) 150 degrees
b) 165 degrees
c) 180 degrees
d) None of these
Question 12: At what time between 7:00 and 8:00 will the minute and hour hands of a clock be pointing at exactly opposite directions?
a) 7:05 minutes 27 seconds
b) 7:07 minutes 16 seconds
c) 7:10 minutes 54 seconds
d) None of these
Question 13: How many times in a day do the minute and hour hands of a clock overlap?
a) 23
b) 24
c) 22
d) None of these
Question 14: A marathon starts between 5pm and 6pm. The referee realizes that the hands of the clock are interchanged when the marathon ends between 8pm and 9pm. What was the approximate duration of the marathon?
a) 2 hours 14 minutes
b) 2 hours 21 minutes
c) 2 hours 46 minutes
d) 2 hours 43 minutes
Question 15: If the hour and minute hands of a clock overlap every 65 minutes, how many minutes does the clock gain or lose every day?
a) 10 10/143 minutes gained
b) 10 10/143 minutes lost
c) 10 minutes gained
d) 10 minutes lost
Question 16: A marathon starts between 5pm and 6pm. The referee realizes that the hands of the clock are interchanged when the marathon ends between 8pm and 9pm. What was the approximate start time of the marathon?
a) 5: 23 pm
b) 5: 42 pm
c) 5: 44 pm
d) 5: 49 pm
Question 17: How many times in twelve hours does the angle between the hour’s and minute’s hand of a clock be exactly one degree at the start of a minute?
a) 2
b) 1
c) 11
d) 22
Question 18: If the minutes and hours hand are identical in a clock. Given that a person checks the time at only integral values of minutes, how many times in a day can a person not be able to find the exact time?
a) 22
b) 20
c) 11
d) 0
Question 19: The hands of two clocks coincide every 60 minutes and 72 minutes respectively. What is the approximate time difference between the two clocks (round to closest minute) after 24 hours as measured by a correct clock?
a) 260 minutes
b) 262 minutes
c) 264 minutes
d) 261 minutes
Question 20: A, B, C, D are standing in clockwise direction at the corners of a square of side ‘s’. They are start running clockwise along the sides of the square with speeds in the ratio 1:2:3:4 respectively. How much distance does A run by the time they all meet for the third time?
a) 11 s
b) 12 s
c) 15 s
d) None of these
100+ Free GK Tests for SSC Exams
Question 21: At what time between 2 o’clock and 3 o’clock will the two hands of the clock be at an angle of 60 degrees?
a) 22 minutes 14 seconds
b) 19 minutes 33 seconds
c) 21 minutes 49 seconds
d) 23 minutes 15 seconds
Question 22: The angle between the minute hand and hour hand of a clock when the time is 7:20 is equal to
a) 45°
b) 90°
c) 100°
d) 120°
Question 23: The angle formed by the hourhand and the minutehand of a clock at 2 : 15 p.m. is
a) 27.5°
b) 45°
c) 22.5°
d) 30°
Question 24: A clock gains 15 minutes per day. If it is set right at 12 noon, the time it shows at 4 AM is
a) 4.20 AM
b) 4.30 AM
c) 4.02 AM
d) 4.10 AM
Question 25: Kanchan bought a clock with 25% discount on marked price. She sold it with 75% gain on the price she bought. What was her profit percentage on the marked price?
a) 31.25
b) 50
c) 56.25
d) 60
1500+ Free SSC Questions & Answers
Answers & Solutions:
1) Answer (D)
The hour hand covers 30° in an hour
$\therefore$ Angle turned in 3$\frac{3}{4}$ hours i.e. $\frac{15}{4}$ hours
= $\frac{15}{4}$ * 30° = $\frac{225^{\circ}}{2}$
= 112$\frac{1^{\circ}}{2}$
2) Answer (C)
Lets take number 12 in clock, as the reference.
hours hand make 30° in 1 hr & (1/2)° in 1 minute.
when the time is 10:40, angle made by hours hand = 10(30)+40(1/2) = 320°
Minute hand makes 30° in every 5 mins==> so in 1 min, it makes 30°/5 = 6°
So in 40 mins, it makes 40*6°=240°
The difference in angles is 320°-240° = 80°
So the answer is option C.
3) Answer (C)
Let the time be 10 hrs x mins.
Lets measure the angle from 12 in clockwise direction,
Angle made by hours hand = 10(360°/12)+x(30°/60) = 10(30°)+x(1/2) = 300°+x/2 —–(1)
Angle made by minutes hand = x(360°/60) = x(6°) ——-(2)
Given that hours hand is nearer to 12 than minutes hand, i.e; hours hand crossed minutes hand
Hence, (1) – (2) = 3°
==>300°+ x/2 – 6x = 3°
==> -11x/2 = -297
==> x = 54
Hence the time will be 10:54
So the answer is option C.
4) Answer (C)
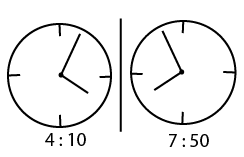
It should be 7:50
So the answer is option C.
5) Answer (B)
8AM to 6PM, 10 hrs
watch gains 6 minutes in one hour,
In 10hrs it gains 10*6 = 60 minutes
Hence at 6PM, it shows 6PM+60mins = 7PM
So the answer is option B.
6) Answer (A)
If clockwise and anti-clockwise directions are considered different, the number of ways of arranging 6 people around a circular table is (6-1)! = 5! = 120 ways
7) Answer (E)
In circular arrangement, there is no distinction among the seats initially. Once the first person sits in one of the seats, all the other seats can be marked based on this reference. The first person can sit in any of the 8 chairs in 1 way (since there is no distinction among the chairs initially). Now, the other 7 people can sit in the 7 remaining chairs in 7! ways.
In general, the number of ways of arranging ‘n’ distinct objects around a circular table is (n-1)!
8) Answer (E)
The person who’ll stand can be selected in 6 ways.
This person can be arranged in any 4 corners in 4 ways.
Remaining 5 can be arranged in a 4! ways around the table.
So total number of ways = 6*4*4! = 576 ways
So E is the right choice.
9) Answer (C)
If two bodies are moving in opposite direction with their speeds in the ratio a: b , the number is distinct points at which they meet on a circular track = a+b
Here the ratio = 20:24 ==>5:6
Therefore number of distinct points = 5+6 = 11
10) Answer (B)
As the two are running in opposite directions, the number of meeting points will be 3+2 = 5 meeting points.
They are as shown on in figure.

Suppose the speeds are 3x and 2x respectively. If A runs clockwise and B counter-clockwise then they will meet at 2L/5, 4L/5, L/5, 3L/5, 5L/5, 2L/5 and so on points.
Hence, 1st point = 2L/5
13th point = L/5
Distance = | 2L/5 – L/5| = L/5 = 120/5 = 24m
Suppose A runs counter-clockwise and B clockwise then they will meet at 3L/5, L/5, 4L/5, 2L/5, 5L/5, 3L/5 and so on points.
Hence, 1st point = 3L/5
13th point = 4L/5
Distance = | 3L/5 – 4L/5| = L/5 = 120/5 = 24m
11) Answer (B)
In thirty minutes, the minute hand covers 180 degrees and hour hand covers 15 degrees. So, angle between the hands is 165 degrees
12) Answer (A)
At a time 7 hours and Y minutes, the hour hand makes an angle of 210+Y/2 degrees and the minutes hand makes an angle of 6Y degrees.
So, we need to solve for Y where
210 + Y/2 = 6Y + 180 or Y = 60/11 minutes which is 5 minutes 27 seconds
13) Answer (C)
In twelve hours, the hands overlap 11 times. So, in a day, they overlap 22 times.
14) Answer (C)
Suppose the marathon started at 5 hours X minutes and ended at 8 hours Y minutes.
Angles made by both the hour’s hands are 150+X/2 and 240+Y/2.
Angles made by the minutes hands are 6X and 6Y.
We know that the difference between the angles made by the hands of the clock is same, so we equate that : 6X – (150 + X/2) = (240 + Y/2) – 6Y => 12X – 300 – X = 480 + Y – 12 Y => 11X + 11Y = 480+300 => X+Y = (780/11) => X+Y $\approx$ 71
We know that the sum of the angles made by the hands of the clock is also same, so we equate that as well : 6X+150+X/2 = 240+Y/2+6Y => 13X + 300 = 480 + 13Y => 13(X-Y) = 180 => X-Y = (180/13) => X-Y = $\approx$ 14
Solving we two equations, we get X = 42.5 mins = 42 mins 30 secs and Y = 28.5 mins = 28 mins 30 secs
Hence, duration of the marathon is = 8:28-5:42 = 2 hours 46 mins.
15) Answer (A)
An hour hand moves 1/2° per minute while a minute hand moves 6° per minute. Hence, a minute hand covers the gap of 11/2° per minute. Hence, an hour hand and minute hand would overlap every 60 mins + 30°/(11/2°) mins = 60m + 60/11 m = 65 5/11 mins.
Hence, in a normal clock, the hour hand and minute hand overlap every 65 5/11 minutes. In the given clock, they overlap every 65 minutes. Hence, the clock gains 5/11 minutes every 65 minutes.
Hence, in 24 hours, the clock would gain = (24*60)*(5/11)/65 = 24*60/143 minutes = 1440/143 minutes = 10 10/143 minutes
16) Answer (B)
Suppose the marathon started at 5 hours X minutes and ended at 8 hours Y minutes. Angle made by hour in the first case will be 150 + 1/2x and the angle made by minute hand will be 6x. In the second case, the angle made by hour hand will be 240 + 1/2y and minute hand will be 6y.
We have been given that 150+ x/2 = 6y and
240 + y/2 = 6x
Solving both the equations we get, x = 42.37 minutes. Start time is 5:42 pm
17) Answer (A)
The angle made by the minute hand against the 12 hour mark after ‘m’ minutes = 360° * (m /60) = 6m
The angle made by the hour hand against the 12 hour mark after ‘h’ hours = 360° * (h /12) = 30h
The angle made by the hour hand against the 12 hour mark after ‘h’ hours and ‘m’ minutes = 30h + 30*m/60 = 30h + m/2
Hence, the condition given is $6m = 30*h + m/2 \pm 1$. We need to find integral solns for this where m<60 and h<12
m = 2/11 (30h-1) or 2/11(30h+1)
The values of h where m is an integer is h=4 m=22 and h=7 m=38.
Thus, there are two solutions (4, 22) and (7, 38). Hence, 2 times in 12 hours.
18) Answer (D)
At any time, A hours and B minutes, the angle made by the hours hand is $30A+B/2.$
Similarly, the angle made by the minutes hand is 6B.
For a person to not be able to find the correct time, there should be another time $A_1:B_1$ such that $30A_1+B_1/2 = 6B$ and $6B_1 = 30A+B/2$.
No integral solutions exist when $0<B<60$
19) Answer (B)
The hands of a correct clock coincide after every 720/11 minutes.
So, 720/11 minutes of the first clock, equal 60 minutes on a correct clock and 720/11 minutes of the second clock equal 72 minutes on a correct clock.
So, in 1 minute on a correct clock, the difference in times of the two clocks is 720/11*[1/60 – 1/72] = 2/11 minutes.
So, time difference in a day is 2880/11 = 262 minutes
20) Answer (A)
In the amount of time taken by A to run one side of the square, D runs all four sides and reaches where he was initially standing. Hence, A and D can only meet at D’s initial position. When A travels 3s, B travels 6s and reaches the point where D is initially standing. Similarly, C travels 9s and reaches D’s starting point. After the first meeting, all three meet after A completes an entire round around the square.
So, total distance covered by A =3s+4s+4s = 11s
21) Answer (C)
The angle between the two hands at 2’o clock is 60 degrees. The speed of the minute hand is 6 deg/min and of the hour hand is 1/2 deg/min. The relative speed between the two hands is 5 and a half degrees/minute. The relative distance that has to be covered is 120 degrees. ( 60 degree initial difference and 60 more ). Therefore, the time needed = 120/5.5 = 120*2/11 = 240/11 = 21 minutes 49 seconds approximately.
22) Answer (C)
Angle between hour hand and minute hand = |30*H – $\frac{11}{2}$*M|
where, H -> hour and M -> minutes
So, at 7:20 => H = 7 & M = 20
=> Angle = 30*7 – $\frac{11}{2}$*20
= 210-110 = 100°
23) Answer (C)
Angle = |$\frac{11}{2}M-30H$| , where M=minutes , H=hours
= |$\frac{11}{2}(15)-30(2)$|
= 22.5
24) Answer (D)
A clock gains 15 minutes per day.
From 12 noon to 4 a.m., time difference = 16 hours
$\because$ 24 hours $\equiv$ 15 minutes
=> 16 hours $\equiv \frac{15}{24} \times 16$ = 10 minutes
$\therefore$ Time shown in watch = 4:10 a.m.
=> Ans – (D)
25) Answer (A)
Let Marked price of clock = Rs. $100x$
Discount % = 25%
=> Price at which Kanchan bought the clock = $100x-(\frac{25}{100}\times100x)=Rs.$ $75x$
Profit % = 75%
=> Price at which Kanchan sold the clock = $75x+(\frac{75}{100}\times75x)$
= $\frac{7}{4}\times75x=Rs.$ $131.25x$
$\therefore$ Profit percentage on the marked price = $\frac{(131.25x-100x)}{100x}\times100$
= $31.25\%$
=> Ans – (A)





