Venn Diagram Questions for CAT

Venn Diagrams is one of the important topics in the CAT Quant/LRDI section. These questions can be a bit challenging, so ensure that you are aware of the Important ways to represent and solve Venn Diagrams in Quant/LRDI. You can check out these CAT Venn Diagrams questions from the CAT Previous year papers. This post will look into some important Venn Diagrams for CAT. These are a good source of practice for CAT preparation; If you want to practice these questions, you can download these Important Venn Diagrams Questions for CAT (with detailed answers) PDF below, which is completely Free.

Download Venn Diagram Questions for CAT

Join CAT 2023 Online Coaching

Instructions

DIRECTIONS for the following two questions: Answer the questions on the basis of the information given below.

New Age Consultants have three consultants Gyani, Medha and Buddhi. The sum of the number of projects handled by Gyani and Buddhi individually is equal to the number of projects in which Medha is involved. All three consultants are involved together in 6 projects. Gyani works with Medha in 14 projects. Buddhi has 2 projects with Medha but without Gyani, and 3 projects with Gyani but without Medha. The total number of projects for New Age Consultants is one less than twice the number of projects in which more than one consultant is involved.

Question 1: What is the number of projects in which Gyani alone is involved?

a) Uniquely equal to zero.

b) Uniquely equal to 1.

c) Uniquely equal to 4.

d) Cannot be determined uniquely.

1) Answer (D)

View Video Solution

Solution:

The total number of projects = 2(3+6+8+2) – 1 = 38 – 1 = 37
So, 19 + 2(x+y) – 16 = 37
=> x+y = 17
The number of projects in which Medha alone is involved is 17-16 = 1
But the number of projects in which Gyani alone is involved cannot be uniquely determined

Question 2: What is the number of projects in which Medha alone is involved?

a) Uniquely equal to zero.

b) Uniquely equal to 1.

c) Uniquely equal to 4.

d) Cannot be determined uniquely.

2) Answer (B)

View Video Solution

Solution:

The total number of projects = 2(3+6+8+2) – 1 = 38 – 1 = 37
So, 19 + 2(x+y) – 16 = 37
=> x+y = 17
The number of projects in which Medha alone is involved is 17-16 = 1
But the number of projects in which Gyani alone is involved cannot be uniquely determined

Question 3: A survey was conducted of 100 people to find out whether they had read recent issues of Golmal, a monthly magazine. The summarized information regarding readership in 3 months is given below:Only September: 18;September but not August: 23;September and July: 8;September:28;July: 48;July and August: 10;none of the three months: 24What is the number of surveyed people who have read exactly two consecutive issues (out of the three)?

a) 7

b) 9

c) 12

d) 14

e) 17

3) Answer (B)

View Video Solution

Solution:

Let the areas be labelled as shown in the diagram above.

The number of people corresponding to “none of the three months” is 24. So, H is 24.

Only September is 18. So, G = 18

September but not August is 23. So, G + D = 23.

Hence, D = 23 – 18 = 5.

We know that September and July is 8. So, D + E = 8

This implies E = 3.

September = 28. So, D + E + F + G = 28.

So, F = 28 – 5 – 3 – 18 = 2.

July and August = 10.

So, B + E = 10.

E = 3. So, B = 7.

July = 48.

So, A + B + D + E = 48

A = 48 – 7 – 5 – 3 = 33.

There are 100 people in total. So, C = 100 – A – B – D – E – F – G – H = 100 – 33 – 7 – 5 – 3 – 2 – 18 – 24 = 8

So, number of people who read exactly two consecutive issues = (July & August) + (August & September) = B + F = 7 + 2 = 9

Instructions

Help Distress (HD) is an NGO involved in providing assistance to people suffering from natural disasters. Currently, it has 37 volunteers. They are involved in three projects: Tsunami Relief (TR) in Tamil Nadu, Flood Relief (FR) in Maharashtra, and Earthquake Relief (ER) in Gujarat. Each volunteer working with Help Distress has to be involved in at least one relief work project.

• A Maximum number of volunteers are involved in the FR project. Among them, the number of volunteers involved in FR project alone is equal to the volunteers having additional involvement in the ER project.

• The number of volunteers involved in the ER project alone is double the number of volunteers involved in all the three projects.

• 17 volunteers are involved in the TR project.

• The number of volunteers involved in the TR project alone is one less than the number ofvolunteers involved in ER project alone.
• Ten volunteers involved in the TR project are also involved in at least one more project.

Question 4: Based on the information given above, the minimum number of volunteers involved in both FR and TR projects, but not in the ER project is:

a) 1

b) 3

c) 4

d) 5

4) Answer (C)

View Video Solution

Solution:

Total number of volunteers are 37

=> 2x+y+x+y+x+y+z+10-z-x+2x-1=37

=> 5x+2y+9=37

=> 5x+2y=28

Also we know that 3x + 2y = 20.

We get x=4, => y=4

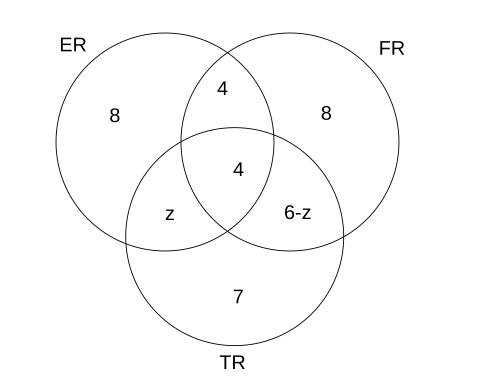
We need to find the minimum value of 6-z, and it is given FR get the most number of volunteers, We get that z cannot be more than 2 because if it is 3 or above ER will have the maximum number of volunteers.

Question 5: Which of the following additional information would enable to find the exact number of volunteers involved in various projects?

a) Twenty volunteers are involved in FR.

b) Four volunteers are involved in all the three projects.

c) Twenty three volunteers are involved in exactly one project.

d) No need for any additional information.

5) Answer (A)

View Video Solution

Solution:

We can get the information mentioned in options B and C using the data given in the passage.

But, we need the information in option A to find the exact number of volunteers in various projects.

Hence, option A is the answer.

Question 6: After some time, the volunteers who were involved in all the three projects were asked to withdraw from one project. As a result, one of the volunteers opted out of the TR project, and one opted out of the ER project, while the remaining ones involved in all the three projects opted out of the FR project. Which of the following statements, then, necessarily follows?

a) The lowest number of volunteers is now in TR project.

b) More volunteers are now in FR project as compared to ER project.

c) More volunteers are now in TR project as compared to ER project.

d) None of the above.

6) Answer (B)

View Video Solution

Solution:

FR is greater than ER, thus z is 4,5,6.

If z=4,

FR=20, ER= 18

If z=5,

FR=21, ER= 17

If z=6,

FR=22, ER= 16

Now even if we transfer one of the volunteers opted out of the TR project thus he will now be handling FR and ER, and one opted out of the ER project will be handling TR and FR, while the remaining ones involved in all the three projects opted out of the FR project.

The worst-case scenario will be when z=4. Now 2 are out of FR, 1 from ER and 1 from TR.

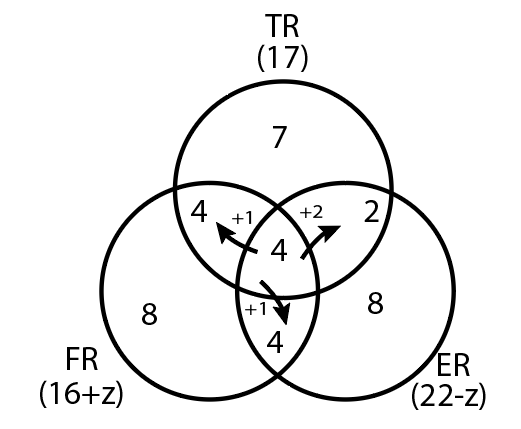
FR=20-2=18 and ER=18-1=17

So we can see that even if volunteers are withdrawn, the number of volunteers in FR are more as in, total if we calculate comes out to be more. Hence option B.

Question 7: After the withdrawal of volunteers, as indicated in the previous question, some new volunteers joined the NGO. Each one of them was allotted only one project in a manner such that, the number of volunteers working in one project alone for each of the three projects became identical. At that point, it was also found that the number of volunteers involved in FR and ER projects was the same as the number of volunteers involved in TR and ER projects. Which of the projects now has the highest number of volunteers?

a) ER

b) FR

c) TR

d) Cannot be determined

7) Answer (A)

View Video Solution

Solution:

Consider p volunteers be added to TR project and q be added to each of FR and ER projects.

Then, 7 + p = 8 + q => p = q + 1

Also, Number of volunteers working on TR = 7 + q + 1 + 4 + 5 = 17 + q

Number of volunteers working on FR = 17 + q

Number of volunteers working on ER = 18 + q.

So if we take any values we get ER  greater than both FR and TR.

Question 8: On her walk through the park, Hamsa collected 50 coloured leaves, all either maple or oak. She sorted them by category when she got home, and found the following:The number of red oak leaves with spots is even and positive.The number of red oak leaves without any spot equals the number of red maple leaves without spots.All non-red oak leaves have spots, and there are five times as many of them as there are red spotted oak leaves.There are no spotted maple leaves that are not red.There are exactly 6 red spotted maple leaves.There are exactly 22 maple leaves that are neither spotted nor red.How many oak leaves did she collect?

a) 22

b) 17

c) 25

d) 18

8) Answer (B)

View Video Solution

Solution:

6+x+22+x+6y/5 = 50
=> 5x + 3y = 55
Since y/5 is even, y should be a multiple of 10
The only possible value is 10
So, y = 10 and x = 5
No. of oak leaves = 17

Question 9: Shyam visited Ram during his brief vacation. In the mornings they both would go for yoga. In the evenings they would play tennis. To have more fun, they indulge only in one activity per day, i.e. either they went for yoga or played tennis each day. There were days when they were lazy and stayed home all day long. There were 24 mornings when they did nothing, 14 evenings when they stayed at home, and a total of 22 days when they did yoga or played tennis. For how many days Shyam stayed with Ram?

a) 32

b) 24

c) 30

d) None of these

9) Answer (C)

View Video Solution

Solution:

Let the number of total days=N
They played tennis for=N-14  days
They did yoga for =N-24 days

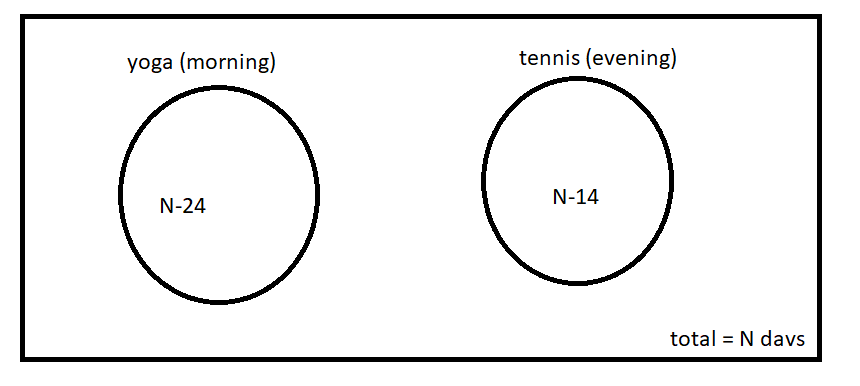
And the question says that total days when they did yoga or played tennis are 22

which means

N-14 + N-24 = 22

2N – 38 = 22

2N = 60

N = 30

Hence total days they stayed together were 30

Question 10: Fifty college teachers are surveyed as to their possession of colour TV, VCR and tape recorder. Of them, 22 own colour TV, 15 own VCR and 14 own tape recorders. Nine of these college teachers own exactly two items out of colour TV, VCR and tape recorder; and, one college teacher owns all three. How many of the 50 teachers own none of the three, colour TV, VCR or tape recorder?

a) 4

b) 9

c) 10

d) 11

10) Answer (C)

View Video Solution

Solution:

Number of people owning exactly 2 articles = 9

Number of people owning exactly 3 articles = 1

Applying AUBUC formula, we get

AUBUC = 22+15+14 – 9 -2*(1)=40

Number of people who do not own any article = 50-40 = 10

Instructions

There were a hundred schools in a town. Of these, the number of schools having a play – ground was 30, and these schools had neither a library nor a laboratory. The number of schools having a laboratory alone was twice the number of those having a library only. The number of schools having a laboratory as well as a library was one-fourth the number of those having a laboratory alone. The number of schools having either a laboratory or a library or both was 35.

Question 11: How many schools had none of the three viz., laboratory, library or play – ground?

a) 20

b) 5

c) 30

d) 35

11) Answer (D)

View Video Solution

Solution:

The diagram for this question has been shown:

Total number of schools having either or LAB or LIB or both = a+b+x/2 – y + y + 3x = 7x/2 + a + b = 35

Here a = b = y = 0

7x/2 = 35

x = 10

Total number of schools having at least one of PG, LIB or LAB = 30+2x+x+x/2 = 30+3x+x/2 = 30+30+5 = 65

Number of schools having neither of the three = 100-65 = 35

Question 12: There are 3 clubs A, B & C in a town with 40, 50 & 60 members respectively. While 10 people are members of all 3 clubs, 70 are members in only one club. How many belong to exactly two clubs?

a) 20

b) 25

c) 50

d) 70

12) Answer (B)

View Video Solution

Solution:

We know that x + y + z = T and x + 2y + 3z = R, where
x = number of members belonging to exactly 1 set = 70
y = number of members belonging to exactly 2 sets
z = number of members belonging to exactly 3 sets = 10
T = Total number of members
R = Repeated total of all the members = (40+50+60) = 150
Thus we have two equations and two unknowns. Solving this we get y = 25

So, 25 people belong to exactly 2 clubs.

Question 13: In a locality, two-thirds of the people have cable TV, one-fifth have VCR, and one-tenth have both. What is the fraction of people having atleast one among cable -TV and VCR?

a) $\frac{19}{30}$

b) $\frac{2}{3}$

c) $\frac{17}{30}$

d) $\frac{23}{30}$

13) Answer (D)

View Video Solution

Solution:

Let the distribution of people having cable TV and VCR be as given in the diagram above.
Hence, $a+c =\frac{2}{3}$
$b+c=\frac{1}{5}$
and $c=\frac{1}{10}$

We need to find $a+b+c=?$
This equals $(a+b)+(b+c)-c = \frac{2}{3}+\frac{1}{5}-\frac{1}{10}$
Which equals $\frac{20+6-3}{30}=\frac{23}{30}$

InstructionsA survey of 200 people in a community who watched at least one of the three channels — BBC, CNN and
DD — showed that 80% of the people watched DD, 22% watched BBC, and 15% watched CNN.

Question 14: What is the maximum percentage of people who can watch all the three channels?

a) 12.5%

b) 8.5%

c) 15%

d) Data insufficient

14) Answer (B)

View Video Solution

Solution:

Let a be the number who watch only one channel, b be the number who watch only 2 channels and c be the number who watch all channels.

a+b+c = 100

a+2b+3c = 80+22+15  =117

Subtracting both equations,

b+2c = 117-100 = 17

Maximum c occurs when b = 0

2c = 17

c = 8.5

Download CAT 2023 Study Plan PDF