CAT Questions on Coordinate Geometry Set-2 PDF
Download important CAT Questions on Coordinate Geometry Set-2 PDF based on previously asked questions in CAT exam. Practice Questions on Coordinate Geometry Set-2 PDF for CAT exam.
Download CAT Questions on Coordinate Geometry Set-2 PDF
Download CAT Quant Questions PDF
Question 1: What is the slope of the line parallel to the line passing through the points (6,3) and (2,1)?
a) 1/2
b) 1
c) 2
d) 1
Question 2: Slope of the line AB is -2/3. Co-ordinates of points A and B are (x , -3) and (5 , 2) respectively. What is the value of x?
a) 4
b) -14
c) 12.5
d) -4
Question 3: What is the slope of the line perpendicular to the line passing through the points (3 , -2) and (4 , 2)?
a) 1/4
b) 4
c) -4
d) -1/4
Question 4: The slopes of two lines are 1 and $\frac{1}{\sqrt{3}}$. What is the angle between these two lines?
a) 15°
b) 30°
c) 45°
d) 60°
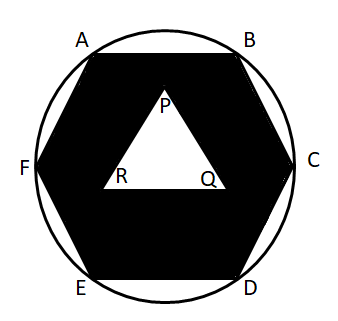
Question 5: ABCDEF is a regular hexagon of side a and PQR is an equilateral triangle. The area of the shaded portion is X and CD : PQ : : 2 : 1. Find the area of the circle circumscribing the hexagon in terms of X.
a) $\frac{16 \pi}{23 \sqrt{3}}$ X
b) $\frac{42 \pi}{5 \sqrt{3}}$ X
c) $\frac{2 \pi}{3 \sqrt{3}}$ X
d) $2\sqrt{3 \pi}$ X
Question 6: In a square of side 2 meters, isosceles triangles of equal area are cut from the corners to form a regular octagon. Find the perimeter and area of the rectangular octagon.
a) $\frac{16}{2+\sqrt{2}};\frac{4(1+\sqrt{2})}{3+2\sqrt{2}}$
b) $\frac{8}{2+\sqrt{2}};\frac{2(1+\sqrt{2})}{3+2\sqrt{2}}$
c) $\frac{16}{1+\sqrt{2}};\frac{3(1+\sqrt{2})}{3+2\sqrt{2}}$
d) None of these
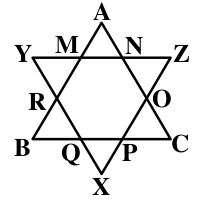
Question 7: $\triangle$ABC and $\triangle$XYZ are equilateral triangles of 54 cm sides. All smaller triangles like $\triangle$ANM, $\triangle$OCP, $\triangle$QPX etc. are also equilateral triangles. Find the area of the shape MNOPQRM.
a) 243√3 sq. cm.
b) 486√3 sq. cm.
c) 729√3 sq. cm.
d) 4374√3 sq. cm.
e) None of the above
Question 8: The centre of a circle inside a triangle is at a distance of 625 cm. from each of the vertices of the triangle. If the diameter of the circle is 350 cm. and the circle is touching only two sides of the triangle, find the area of the triangle.
a) 240000
b) 387072
c) 480000
d) 506447
e) None of the above
Question 9: The figure shows a circle of diameter AB and radius 6.5 cm. If chord CA is 5 cm long, find the area of triangle ABC.

a) 60 sq. cm
b) 30 sq. cm
c) 40 sq. cm
d) 52 sq. cm
Question 10: Two diagonals of a parallelogram intersect each other at coordinates (17.5, 23.5). Two adjacent points of the parallelogram are (5.5, 7.5) and (13.5, 16). Find the lengths of the diagonals.
a) 15 and 30
b) 15 and 40
c) 17 and 30
d) 17 and 40
e) Multiple solutions are possible
Download CAT Quant Questions PDF
Answers & Solutions:
1) Answer (A)
Slope of line passing through points (2,1) and (6,3)
= $\frac{3 – 1}{6 – 2} = \frac{2}{4} = \frac{1}{2}$
Slope of two parallel lines is always equal.
=> Slope of the line parallel to the line having slope 1/2 = $\frac{1}{2}$
=> Ans – (A)
2) Answer (C)
slope = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{2+3}{5-x}=\frac{5}{5-x}=\frac{-2}{3}$
$\rightarrow 15 = -10 + 2x$
$\rightarrow x = \frac{25}{2} = 12.5$
so the answer is option C.
3) Answer (D)
slope m = $\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{2+2}{4-3}=4$
slope of the perpendicular line = -1/m = -1/4.
So the answer is option D.
4) Answer (A)
Slope of the two lines, $m_1=1$ and $m_2=\frac{1}{\sqrt{3}}$
Let angle between them = $\theta$
Then, $tan(\theta)=|\frac{m_1-m_2}{1+m_1m_2}|$
=> $tan(\theta) = \frac{1-\frac{1}{\sqrt{3}}}{1+\frac{1}{\sqrt{3}}}$
=> $tan(\theta)=\frac{tan(45)-tan(30)}{1+tan(45)tan(30)}$
=> $tan(\theta)=tan(45-30)$ $\because [tan(A-B)=\frac{tanA-tanB}{1+tanAtanB}]$
=> $\theta = 15$°
=> Ans – (A)
5) Answer (A)
Let ‘a’ be the length of side of the hexagon. Therefore, the area of hexagon = $6*\dfrac{\sqrt{3}}{4}\times a^2$.
The area of triangle PQR = $\dfrac{\sqrt{3}}{4}\times (a/2)^2$
Therefore, the are of the shaded region = $6*\dfrac{\sqrt{3}}{4}\times a^2$ – $\dfrac{\sqrt{3}}{4}\times (a/2)^2$ = $\dfrac{23\sqrt{3}a^2}{16} = X$
$\Rightarrow$ $a^2 = \dfrac{16X}{23\sqrt{3}}$
The area of the circle = $\pi*a^2$
$\Rightarrow$ $\dfrac{16 \pi}{23 \sqrt{3}}$ X. Hence, option A is the correct answer.
Download CAT Quant Questions PDF
6) Answer (D)
Let us assume that ‘a’ is the length of the side of equal sides of the isosceles triangle.
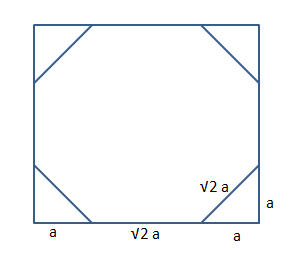
We can see that $a+\sqrt{2}*a+a=2$
$\Rightarrow$ a = $\dfrac{2}{2+\sqrt{2}}$
Therefore, the perimeter of the regular octagon = $8*a*\sqrt{2}$
$\Rightarrow$ $\dfrac{8\sqrt{2}*2}{2+\sqrt{2}}$
$\Rightarrow$ $\dfrac{16}{1+\sqrt{2}}$ … (1)
Area of regular octagon = $2x^2(1+\sqrt{2})$ where ‘x’ is the length of each side.
Here, x = $a\sqrt{2}$ = $\dfrac{2\sqrt{2}}{2+\sqrt{2}}$ = $\dfrac{2}{1+\sqrt{2}}$
Therefore, area of the regular octagon = $2*(\dfrac{2}{1+\sqrt{2}})^2(1+\sqrt{2})$ = $\dfrac{8}{1+\sqrt{2}}$ =$\dfrac{8}{1+\sqrt{2}}*\dfrac{1+\sqrt{2}}{1+\sqrt{2}}$ = $\dfrac{8*(1+\sqrt{2})}{3+2\sqrt{2}}$
Hence, we can say that none of the given answer is correct.
7) Answer (B)
AB = 54 cm and $\triangle$ANM , $\triangle$OCP , $\triangle$OPX are equilateral triangles.
=> MN = MR = NO = OP = PQ = QR = $\frac{54}{3} = 18$ cm
Thus, MNOPQRM is a regular hexagon with side 18 cm
$\therefore$ Area of MNOPQRM = $\frac{3 \sqrt{3}}{2} (side)^2$
= $\frac{3 \sqrt{3}}{2} \times 18^2 = 486 \sqrt{3} cm^2$
8) Answer (B)

If a point is equidistant from all 3 vertices, it has to be the circumcentre. The given circle with centre S is concentric and touches two sides.
As S is equidistant from 2 of the sides (say AB and AC), => It lies on angle bisector of $\angle A$.
=> $\triangle ABC$ is isosceles with AB = AC
Radius of the circle = RS = SQ = 175 cm and SA = SB = SC = 625 cm
=> $AR = \sqrt{625^2 – 175^2} = 600$
Let SP = x
=> $(BP)^2 = (BA)^2 – (AP)^2 = (BS)^2 – (SP)^2$
=> $1200^2 – (625 + x)^2 = 625^2 – x^2$
=>$1200^2 – 625^2 – x^2 – 2*625x = 625^2 – x^2$
=> $1200^2 – 2 * 625^2 = 1250x$
=> $x = \frac{658750}{1250} = 527$
=> $BP = \sqrt{625^2 – 527^2} = 336$
$\therefore$ ar $(\triangle ABC)$ = $\triangle ASB + \triangle ASC + \triangle SBC$
= $(600 \times 175) + (600 \times 175) + (527 \times 336)$
= $105000 + 105000 + 177072 = 387072$
9) Answer (B)
According to given dimensions, triangle will be a right angled triangle.
So BC = 12
And area = $\frac{1}{2} \times 12 \times 5$
= 30
10) Answer (D)

Using distance formula,
$CX = \sqrt{(17.5 – 5.5)^2 + (23.5 – 7.5)^2} = \sqrt{12^2 + 16^2}$
= $\sqrt{144 + 256} = \sqrt{400} = 20$
=> $AC = 2 \times CX = 40$
$BX = \sqrt{(17.5 – 13.5)^2 + (23.5 – 16)^2} = \sqrt{4^2 + 7.5^2}$
= $\sqrt{16 + 56.25} = \sqrt{72.25} = 8.5$
=> $BD = 2 \times BX = 17$
Download CAT Previous Papers PDF
Download Free CAT Preparation App
We hope this Coordinate Geometry Set-2 Questions PDF for CAT with Solutions will be helpful to you.





![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)