CAT Probability Questions PDF [Most Important]

Probability topic an important part of the CAT. You can expect close to 2-3 questions in the latest 22 question format of the CAT Quant section. In this article, we will look into some Probability Questions for the CAT Exam. If you want to practice these important probability questions, you can download the PDF, which is completely Free.

• Probability is often one of the most feared topics among the candidates. It is not a very difficult topic if you understand the basics of Probability well.
• Probability-based questions appear in the CAT test almost every year. A lot of aspirants avoid this topic but remember that one can definitely solve the easy questions on Probability if one is thorough with the basics. Therefore, practising questions with Probability should not be avoided.
• The chances of occurring or not occurring an event should be determined based on the number of favourable and not favourable conditions.
• Here we are giving some very important probability questions, which also include questions from the CAT previous papers. The candidates are advised to try each question on their own and later go through the solutions given below.

Download important CAT Questions on Probability PDF based on previously asked questions in the CAT exam. Practice Probability Questions PDF for CAT exam.

Download Probability Questions for CAT

Enroll for CAT 2022 Crash Course

Question 1: A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is

1) Answer: 50

View Video Solution

Solution:

The question asks for the number of 4 digit numbers using only the digits 1, 2, and 3 such that the digits 2 and 3 appear at least once.

The different possibilities include :

Case 1:The four digits are ( 2, 2, 2, 3). Since the number 2 is repeated 3 times. The total number of arrangements are :

$\frac{4!}{3!}$ = 4.

Case 2: The four digits are 2, 2, 3, 3. The total number of four-digit numbers formed using this are :

$\frac{4!}{2!\cdot2!}=\ 6$

Case 3: The four digits are 2, 3, 3, 3. The number of possible 4 digit numbers are :

$\frac{4!}{3!}$ = 4

Case4: The four digits are 2, 3, 3, 1. The number of possible 4 digit numbers are :

$\frac{4!}{2!}=\ 12$

Case5: Using the digits 2, 2, 3, 1. The number of possible 4 digit numbers are :

$\frac{4!}{2!}=\ 12$

Case 6: Using the digits 2, 3, 1, 1. The number of possible 4 digit numbers are :

$\frac{4!}{2!}=\ 12$

A total of 12 + 12 + 12 + 4 + 6 + 4 = 50 possibilities.

Alternatively

We have to form 4 digit numbers using 1,2,3 such that 2,3 appears at least once
So the possible cases :

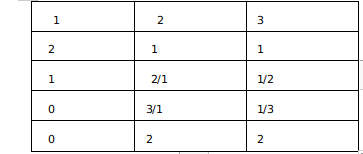
Now we get $\frac{4!}{2!}\times\ 3$= 36 ( When one digit is used twice and the remaining two once )
$\frac{4!}{3!}\times\ 2$ = 8 ( When 1 is used 0 times and 2 and 3 is used 3 times or 1 time )
$\frac{4!}{2!\times\ 2!}=\ 6$( When 2 and 3 is used 2 times each )
So total numbers = 36+8+6 =50

Question 2: The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at least four balloons and one pencil, is

2) Answer: 1000

View Video Solution

Solution:

This question is an application of the product rule in probability and combinatorics.

In the product rule, if two events A and B can occur in x and y ways, and for an event E, both events A and B need to take place, the number of ways that E can occur is xy. This can be expanded to 3 or more events as well.

Event 1: Distribution of balloons

Since each child gets at least 4 balloons, we will initially allocate these 4 balloons to each of them.

So we are left with 15 – 4 x 3 = 15 – 12 = 3 balloons and 3 children.

Now we need to distribute 3 identical balloons to 3 children.

This can be done in $^{n+r-1}C_{r-1}$ ways, where n = 3 and r = 3.

So, number of ways = $^{3+3-1}C_{3-1}=^5C_2=\frac{5\times\ 4}{2\times\ 1}=10$

Event 2: Distribution of pencils

Since each child gets at least one pencil, we will allocate 1 pencil to each child. We are now left with 6 – 3 = 3 pencils.

We now need to distribute 3 identical pencils to 3 children.

This can be done in $^{n+r-1}C_{r-1}$ ways, where n = 3 and r = 3.

So, number of ways = $^{3+3-1}C_{3-1}=^5C_2=\frac{5\times\ 4}{2\times\ 1}=10$

Event 3: Distribution of erasers

We need to distribute 3 identical erasers to 3 children.

This can be done in $^{n+r-1}C_{r-1}$ ways, where n = 3 and r = 3.

So, number of ways = $^{3+3-1}C_{3-1}=^5C_2=\frac{5\times\ 4}{2\times\ 1}=10$

Applying the product rule, we get the total number of ways = 10 x 10 x 10 = 1000.

Question 3: How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order?

3) Answer: 70

View Video Solution

Solution:

Let the numbers be of the form 100a+10b+c, where a, b, and c represent single digits.

Then (100c+10b+a)-(100a+10b+c)=198

99c-99a=198

c-a = 2.

Now, a can take the values 1-7. a cannot be zero as the initial number has 3 digits and cannot be 8 or 9 as then c would not be a single-digit number.

Thus, there can be 7 cases.

B can take the value of any digit from 0-9, as it does not affect the answer. Hence, the total cases will be $7\times\ 10=70$.

Question 4: The number of groups of three or more distinct numbers that can be chosen from 1, 2, 3, 4, 5, 6, 7 and 8 so that the groups always include 3 and 5, while 7 and 8 are never included together is

4) Answer: 47

View Video Solution

Solution:

The possible arrangements are of the form

35 _ Can be chosen in 6 ways.

35 _ _ We can choose 2 out of the remaining 6 in $^6C_2=15$ways. We remove 1 case where 7 and 8 are together to get 14 ways.

35 _ _ _We can choose 3 out of the remaining 6 in $^6C_3=20$ways. We remove 4 cases where 7 and 8 are together to get 16 ways.

35 _ _ _ _We can choose 4 out of the remaining 6 in $^6C_4=15$ways. We remove 6 case where 7 and 8 are together to get 9 ways.

35 _ _ _ _ _ We choose 1 out of 7 and 8 and all the remaining others in 2 ways.

Thus, total number of cases = 6+14+16+9+2 = 47.

Alternatively,

The arrangement requires a selection of 3 or more numbers while including 3 and 5 and 7, 8 are never included together. We have cases including a selection of only 7, only 8 and neither 7 nor 8.

Considering the cases, only 7 is selected.

We can select a maximum of 7 digit numbers. We must select 3, 5, and 7.

Hence we must have ( 3, 5, 7) for the remaining 4 numbers we have

Each of the numbers can either be selected or not selected and we have 4 numbers :

Hence we have _ _ _ _ and 2 possibilities for each and hence a total of 2*2*2*2 = 16 possibilities.

SImilarly, including only 8, we have 16 more possibilities.

Cases including neither 7 nor 8.

We must have 3 and 5 in the group but there must be no 7 and 8 in the group.

Hence we have 3 5 _ _ _ _.

For the 4 blanks, we can have 2 possibilities for either placing a number or not among 1, 2, 4, 6.

= 16 possibilities

But we must remove the case where neither of the 4 numbers are placed because the number becomes a two-digit number.

Hence 16 – 1 = 15 cases.

Total = 16+15+16 = 47 possibilities

Question 5: With rectangular axes of coordinates, the number of paths from (1, 1) to (8, 10) via (4, 6), where each step from any point (x, y) is either to (x, y+1) or to (x+1, y), is

5) Answer: 3920

View Video Solution

Solution:

The number of paths from (1, 1) to (8, 10) via (4, 6) = The number of paths from (1,1) to (4,6) * The number of paths from (4,6) to (8,10)

To calculate the number of paths from (1,1) to (4,6), 4-1 =3 steps in x-directions and 6-1=5 steps in y direction

Hence the number of paths from (1,1) to (4,6) = $^{(3+5)}C_3$ = 56

To calculate the number of paths from (4,6) to (8,10), 8-4 =4 steps in x-directions and 10-6=4 steps in y direction

Hence the number of paths from (4,6) to (8,10) = $^{(4+4)}C_4$ = 70

The number of paths from (1, 1) to (8, 10) via (4, 6) = 56*70=3920

Checkout: CAT Free Practice Questions and Videos

Question 6: In a tournament, there are 43 junior level and 51 senior level participants. Each pair of juniors play one match. Each pair of seniors play one match. There is no junior versus senior match. The number of girl versus girl matches in junior level is 153, while the number of boy versus boy matches in senior level is 276. The number of matches a boy plays against a girl is

6) Answer: 1098

View Video Solution

Solution:

In a tournament, there are 43 junior level and 51 senior level participants.

Let ‘n’ be the number of girls on junior level. It is given that the number of girl versus girl matches in junior level is 153.

$\Rightarrow$ nC2 = 153

$\Rightarrow$ n(n-1)/2 = 153

$\Rightarrow$ n(n-1) = 306

=> n$^{2}$-n-306 = 0

=> (n+17)(n-18)=0

=> n=18  (rejecting n=-17)

Therefore, number of boys on junior level = 43 – 18 = 25.

Let ‘m’ be the number of boys on senior level. It is given that the number of boy versus boy matches in senior level is 276.

$\Rightarrow$ mC2 = 276

$\Rightarrow$ m = 24

Therefore, number of girls on senior level = 51 – 24 = 27.

Hence, the number of matches a boy plays against a girl  = 18*25+24*27 = 1098

Question 7: How many two-digit numbers, with a non-zero digit in the units place, are there which are more than thrice the number formed by interchanging the positions of its digits?

7) Answer: 6

View Video Solution

Solution:

Let ‘ab’ be the two digit number. Where b $\neq$ 0.

We will get number ‘ba’ after interchanging its digit.

It is given that 10a+b > 3*(10b + a)

7a > 29b

If b = 1, then a = {5, 6, 7, 8, 9}

If b = 2, then a = {9}

If b = 3, then no value of ‘a’ is possible. Hence, we can say that there are a total of 6 such numbers.

Question 8: How many numbers with two or more digits can be formed with the digits 1,2,3,4,5,6,7,8,9, so that in every such number, each digit is used at most once and the digits appear in the ascending order?

8) Answer: 502

View Video Solution

Solution:

It has been given that the digits in the number should appear in the ascending order. Therefore, there is only 1 possible arrangement of the digits once they are selected to form a number.
There are 9 numbers (1,2,3,4,5,6,7,8,9) in total.
2 digit numbers can be formed in $9C_2$ ways.
3 digit numbers can be formed in $9C_3$ ways.
…………………………………………..
..9 digit number can be formed in 9C9 ways.

We know that $nC_0+nC_1+nC_2+………+nC_n =2^n$
=> $9C_0 + 9C_1+9C_2+….9C_9 = 2^9$
$9C_0 + 9C_1 + …9C_9 = 512$

We have to subtract $9C_0$ and $9C_1$ from both the sides of the equations since we cannot form single digit numbers.
=> $9C_2 + 9C_3+…+9C_9=512-1-9$
$9C_2+9C_3+…+9C_9=502$

Therefore, $502$ is the right answer.

Question 9: How many four digit numbers, which are divisible by 6, can be formed using the digits 0, 2, 3, 4, 6, such that no digit is used more than once and 0 does not occur in the left-most position?

9) Answer: 50

View Video Solution

Solution:

For the number to be divisible by 6, the sum of the digits should be divisible by 3 and the units digit should be even. Hence we have the digits as

Case I: 2, 3, 4, 6
Now the units place can be filled in three ways (2,4,6), and the remaining three places can be filled in 3! = 6 ways.
Hence total number of ways = 3*6 = 18

Case II: 0, 2, 3, 4
case II a: 0 is in the units place => 3! = 6 ways
case II b: 0 is not in the units place => units place can be filled in 2 ways( 2,4) , thousands place can be filled in 2 ways ( remaining 3 – 0) and remaining can be filled in 2! = 2 ways. Hence total number of ways = 2 * 2 * 2 = 8
Total number of ways in this case = 6 + 8 = 14 ways.

Case III: 0, 2, 4, 6
case III a: 0 is in the units place => 3! = 6 ways

case II b: 0 is not in the units place => units place can be filled in 3 ways( 2,4,6) , thousands place can be filled in 2 ways (remaining 3 – 0) and remaining can be filled in 2! = 2 ways. Hence total number of ways = 3 * 2 * 2 = 12
Total number of ways in this case = 6 + 12= 18 ways.

Hence the total number of ways = 18 + 14  + 18 = 50 ways

Question 10: In how many ways can 8 identical pens be distributed among Amal, Bimal, and Kamal so that Amal gets at least 1 pen, Bimal gets at least 2 pens, and Kamal gets at least 3 pens?

10) Answer: 6

View Video Solution

Solution:

After Amal, Bimal and Kamal are given their minimum required pens, the pens left are 8 – (1 + 2 + 3) = 2 pens
Now these two pens have to be divided between three persons so that each person can get zero pens = $^{2+3-1}C_{3-1}$ = $^4C_2$  = 6