CAT Logical Reasoning Questions [Most Important]
CAT LRDI is one of the three key sections in the CAT exam. This section is a deciding factor for many MBA aspirants. It is essential that you solve more LR sets during your practice. Also, do check out all the CAT LR sets from the CAT Previous Papers with detailed video solutions. This article will look into some important CAT LR questions for the CAT Exam. If you want to practice these important CAT LR questions PDF, you can download the PDF given below, which is completely Free.
Instructions
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
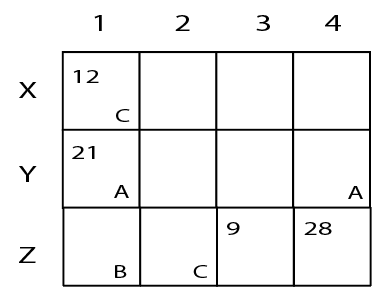
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Question 1: Which column had the highest number of trees?
a) 4
b) 3
c) Cannot be determined
d) 2
1) Answer (A)
Solution:
There are 12 plots and each of them got even number of plots. So, possible cases are 4,4,2,2 or 6,2,2,2.
From 4, A and B got more plots than D. So, the only possible case is A, B each got 4 and C,D each got 2.
From 6, D has to get two adjacent plots and From 8, plots of C, D are
nit adjacent to each other => D must have got plots in X3, X4.
C already has two plots in X1, Z2. So, the corner plot Z4 should belong to B.
From 7, B has a plot in each row and each column. So, X2 should belong to B.
Now, out of the remaining Y2, Y3, Y4 and Z3 three plots belong to A and one belongs to B.
Till now B hasn’t got any plot in Third column and 2nd row.
So, Y3 belongs to B and Y2, Y4, Z3 belongs to A.
Let the number of trees in Y4 be 4x from 3, number of trees in Y3, Y2 will be 2x, x respectively.
The number of teak trees=7x+21
.’. Number of mango trees=14x+42
The table now looks like:

Each plot had trees in non-zero multiples of 3 or 4 and none of the
plots had the same number of trees and from 2, B didn’t have the largest
number of trees in a plot => x<8.
x can’t be 7,5,3,2,1 as for these cases at least one of x,2x,4x is neither multiple of 3 or 4.
x can be 6 or 4.
If x=6, number of Teak trees will be 63 and Mango trees will be 126
=> Number of Pine trees= 205-126-63=16 but number of trees in
Z3+Z4>16 so, x$\ne\ $6.
If x=4, Number of Teak trees=49 and Mango trees=98 => Number of Pine trees=58. Valid case.
Number of trees with A= 30+5x=50.
From 1, number of trees with C, D= 30, 56 respectively.
So, number of trees in Z2= 18.
.’. Number of trees with B= 205-50-30-56=69.
From 2, largest number of trees in a plot is 32. They can be in the
plot of either B or D. If they are from B, they have to be from X2 but
in that case number of trees in Z1=1 which is neither a multiple of 3 or
4.
So, highest number of trees in a plot are with D and it is 32 -=> number of trees in X3, X4 are 32, 24 in any order.
So, number of trees in X2= 98-56-12=30
.’. Number of trees in Z1=69-30-28-8=3.
The final table will look like:
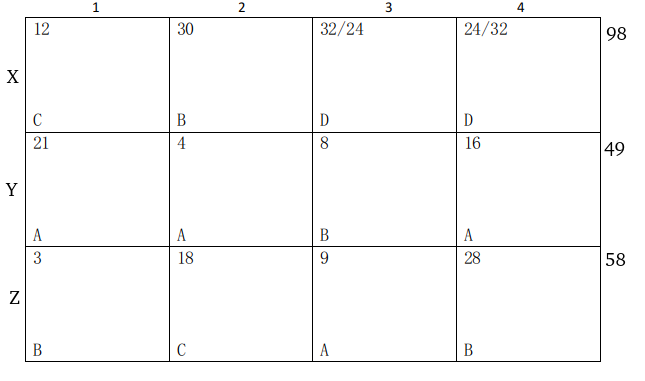
Column 1,2,3,4 have 36, 52, 49, 68 trees respectively.
Hence A is correct answer.
Question 2: Which of the following statements is NOT true?
a) Chitra got 12 mango trees
b) Bina got 32 pine trees.
c) Abha got 41 teak trees.
d) Dipti got 56 mango trees
2) Answer (B)
Solution:
There are 12 plots and each of them got even number of plots. So, possible cases are 4,4,2,2 or 6,2,2,2.
From 4, A and B got more plots than D. So, the only possible case is A, B each got 4 and C,D each got 2.
From 6, D has to get two adjacent plots and From 8, plots of C, D are
nit adjacent to each other => D must have got plots in X3, X4.
C already has two plots in X1, Z2. So, the corner plot Z4 should belong to B.
From 7, B has a plot in each row and each column. So, X2 should belong to B.
Now, out of the remaining Y2, Y3, Y4 and Z3 three plots belong to A and one belongs to B.
Till now B hasn’t got any plot in Third column and 2nd row.
So, Y3 belongs to B and Y2, Y4, Z3 belongs to A.
Let the number of trees in Y4 be 4x from 3, number of trees in Y3, Y2 will be 2x, x respectively.
The number of teak trees=7x+21
.’. Number of mango trees=14x+42
The table now looks like:

Each plot had trees in non-zero multiples of 3 or 4 and none of the
plots had the same number of trees and from 2, B didn’t have the largest
number of trees in a plot => x<8.
x can’t be 7,5,3,2,1 as for these cases at least one of x,2x,4x is neither multiple of 3 or 4.
x can be 6 or 4.
If x=6, number of Teak trees will be 63 and Mango trees will be 126
=> Number of Pine trees= 205-126-63=16 but number of trees in
Z3+Z4>16 so, x$\ne\ $6.
If x=4, Number of Teak trees=49 and Mango trees=98 => Number of Pine trees=58. Valid case.
Number of trees with A= 30+5x=50.
From 1, number of trees with C, D= 30, 56 respectively.
So, number of trees in Z2= 18.
.’. Number of trees with B= 205-50-30-56=69.
From 2, largest number of trees in a plot is 32. They can be in the
plot of either B or D. If they are from B, they have to be from X2 but
in that case number of trees in Z1=1 which is neither a multiple of 3 or
4.
So, highest number of trees in a plot are with D and it is 32 -=> number of trees in X3, X4 are 32, 24 in any order.
So, number of trees in X2= 98-56-12=30
.’. Number of trees in Z1=69-30-28-8=3.
The final table will look like:

Bina got 28 pine trees, Option B is correct answer.
Question 3: Who got the plot with the smallest number of trees and how many trees did that plot have?
a) Dipti, 6 trees
b) Bina, 3 trees
c) Bina, 4 trees
d) Abha, 4 trees
3) Answer (B)
Solution:
There are 12 plots and each of them got even number of plots. So, possible cases are 4,4,2,2 or 6,2,2,2.
From 4, A and B got more plots than D. So, the only possible case is A, B each got 4 and C,D each got 2.
From 6, D has to get two adjacent plots and From 8, plots of C, D are
nit adjacent to each other => D must have got plots in X3, X4.
C already has two plots in X1, Z2. So, the corner plot Z4 should belong to B.
From 7, B has a plot in each row and each column. So, X2 should belong to B.
Now, out of the remaining Y2, Y3, Y4 and Z3 three plots belong to A and one belongs to B.
Till now B hasn’t got any plot in Third column and 2nd row.
So, Y3 belongs to B and Y2, Y4, Z3 belongs to A.
Let the number of trees in Y4 be 4x from 3, number of trees in Y3, Y2 will be 2x, x respectively.
The number of teak trees=7x+21
.’. Number of mango trees=14x+42
The table now looks like:

Each plot had trees in non-zero multiples of 3 or 4 and none of the
plots had the same number of trees and from 2, B didn’t have the largest
number of trees in a plot => x<8.
x can’t be 7,5,3,2,1 as for these cases at least one of x,2x,4x is neither multiple of 3 or 4.
x can be 6 or 4.
If x=6, number of Teak trees will be 63 and Mango trees will be 126
=> Number of Pine trees= 205-126-63=16 but number of trees in
Z3+Z4>16 so, x$\ne\ $6.
If x=4, Number of Teak trees=49 and Mango trees=98 => Number of Pine trees=58. Valid case.
Number of trees with A= 30+5x=50.
From 1, number of trees with C, D= 30, 56 respectively.
So, number of trees in Z2= 18.
.’. Number of trees with B= 205-50-30-56=69.
From 2, largest number of trees in a plot is 32. They can be in the
plot of either B or D. If they are from B, they have to be from X2 but
in that case number of trees in Z1=1 which is neither a multiple of 3 or
4.
So, highest number of trees in a plot are with D and it is 32 -=> number of trees in X3, X4 are 32, 24 in any order.
So, number of trees in X2= 98-56-12=30
.’. Number of trees in Z1=69-30-28-8=3.
The final table will look like:

.’. Number of trees per plot is least for Benna=3.
Question 4: How many pine trees did Chitra receive?
a) 18
b) 30
c) 21
d) 15
4) Answer (A)
Solution:
There are 12 plots and each of them got even number of plots. So, possible cases are 4,4,2,2 or 6,2,2,2.
From 4, A and B got more plots than D. So, the only possible case is A, B each got 4 and C,D each got 2.
From 6, D has to get two adjacent plots and From 8, plots of C, D are
nit adjacent to each other => D must have got plots in X3, X4.
C already has two plots in X1, Z2. So, the corner plot Z4 should belong to B.
From 7, B has a plot in each row and each column. So, X2 should belong to B.
Now, out of the remaining Y2, Y3, Y4 and Z3 three plots belong to A and one belongs to B.
Till now B hasn’t got any plot in Third column and 2nd row.
So, Y3 belongs to B and Y2, Y4, Z3 belongs to A.
Let the number of trees in Y4 be 4x from 3, number of trees in Y3, Y2 will be 2x, x respectively.
The number of teak trees=7x+21
.’. Number of mango trees=14x+42
The table now looks like:

Each plot had trees in non-zero multiples of 3 or 4 and none of the
plots had the same number of trees and from 2, B didn’t have the largest
number of trees in a plot => x<8.
x can’t be 7,5,3,2,1 as for these cases at least one of x,2x,4x is neither multiple of 3 or 4.
x can be 6 or 4.
If x=6, number of Teak trees will be 63 and Mango trees will be 126
=> Number of Pine trees= 205-126-63=16 but number of trees in
Z3+Z4>16 so, x$\ne\ $6.
If x=4, Number of Teak trees=49 and Mango trees=98 => Number of Pine trees=58. Valid case.
Number of trees with A= 30+5x=50.
From 1, number of trees with C, D= 30, 56 respectively.
So, number of trees in Z2= 18.
.’. Number of trees with B= 205-50-30-56=69.
From 2, largest number of trees in a plot is 32. They can be in the
plot of either B or D. If they are from B, they have to be from X2 but
in that case number of trees in Z1=1 which is neither a multiple of 3 or
4.
So, highest number of trees in a plot are with D and it is 32 -=> number of trees in X3, X4 are 32, 24 in any order.
So, number of trees in X2= 98-56-12=30
.’. Number of trees in Z1=69-30-28-8=3.
The final table will look like:

Number of PIne trees received by Chitra = 18.
Question 5: Which of the following is the correct sequence of trees received by Abha, Bina, Chitra and Dipti in that order?
a) 50, 69, 30, 56
b) 54, 57, 34, 60
c) 44, 87, 24, 50
d) 60, 39, 40, 66
5) Answer (A)
Solution:
There are 12 plots and each of them got even number of plots. So, possible cases are 4,4,2,2 or 6,2,2,2.
From 4, A and B got more plots than D. So, the only possible case is A, B each got 4 and C,D each got 2.
From 6, D has to get two adjacent plots and From 8, plots of C, D are
nit adjacent to each other => D must have got plots in X3, X4.
C already has two plots in X1, Z2. So, the corner plot Z4 should belong to B.
From 7, B has a plot in each row and each column. So, X2 should belong to B.
Now, out of the remaining Y2, Y3, Y4 and Z3 three plots belong to A and one belongs to B.
Till now B hasn’t got any plot in Third column and 2nd row.
So, Y3 belongs to B and Y2, Y4, Z3 belongs to A.
Let the number of trees in Y4 be 4x from 3, number of trees in Y3, Y2 will be 2x, x respectively.
The number of teak trees=7x+21
.’. Number of mango trees=14x+42
The table now looks like:

Each plot had trees in non-zero multiples of 3 or 4 and none of the
plots had the same number of trees and from 2, B didn’t have the largest
number of trees in a plot => x<8.
x can’t be 7,5,3,2,1 as for these cases at least one of x,2x,4x is neither multiple of 3 or 4.
x can be 6 or 4.
If x=6, number of Teak trees will be 63 and Mango trees will be 126
=> Number of Pine trees= 205-126-63=16 but number of trees in
Z3+Z4>16 so, x$\ne\ $6.
If x=4, Number of Teak trees=49 and Mango trees=98 => Number of Pine trees=58. Valid case.
Number of trees with A= 30+5x=50.
From 1, number of trees with C, D= 30, 56 respectively.
So, number of trees in Z2= 18.
.’. Number of trees with B= 205-50-30-56=69.
From
2, largest number of trees in a plot is 32. They can be in the plot of
either B or D. If they are from B, they have to be from X2 but in that
case number of trees in Z1=1 which is neither a multiple of 3 or 4.
So, highest number of trees in a plot are with D and it is 32 -=> number of trees in X3, X4 are 32, 24 in any order.
So, number of trees in X2= 98-56-12=30
.’. Number of trees in Z1=69-30-28-8=3.
The final table will look like:

Sequence of trees received by Abha, Bina, Chitra and Dipti is 50,69,30,56.
Checkout: CAT Free Practice Questions and Videos
Question 6: How many mango trees were there in total?
a) 49
b) 84
c) 98
d) 126
6) Answer (C)
Solution:
There are 12 plots and each of them got even number of plots. So, possible cases are 4,4,2,2 or 6,2,2,2.
From 4, A and B got more plots than D. So, the only possible case is A, B each got 4 and C,D each got 2.
From 6, D has to get two adjacent plots and From 8, plots of C, D are nit adjacent to each other => D must have got plots in X3, X4.
C already has two plots in X1, Z2. So, the corner plot Z4 should belong to B.
From 7, B has a plot in each row and each column. So, X2 should belong to B.
Now, out of the remaining Y2, Y3, Y4 and Z3 three plots belong to A and one belongs to B.
Till now B hasn’t got any plot in Third column and 2nd row.
So, Y3 belongs to B and Y2, Y4, Z3 belongs to A.
Let the number of trees in Y4 be 4x from 3, number of trees in Y3, Y2 will be 2x, x respectively.
The number of teak trees=7x+21
.’. Number of mango trees=14x+42
The table now looks like:

Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees and from 2, B didn’t have the largest number of trees in a plot => x<8.
x can’t be 7,5,3,2,1 as for these cases at least one of x,2x,4x is neither multiple of 3 or 4.
x can be 6 or 4.
If x=6, number of Teak trees will be 63 and Mango trees will be 126 => Number of Pine trees= 205-126-63=16 but number of trees in Z3+Z4>16 so, x$\ne\ $6.
If x=4, Number of Teak trees=49 and Mango trees=98 => Number of Pine trees=58. Valid case.
Number of trees with A= 30+5x=50.
From 1, number of trees with C, D= 30, 56 respectively.
So, number of trees in Z2= 18.
.’. Number of trees with B= 205-50-30-56=69.
From 2, largest number of trees in a plot is 32. They can be in the plot of either B or D. If they are from B, they have to be from X2 but in that case number of trees in Z1=1 which is neither a multiple of 3 or 4.
So, highest number of trees in a plot are with D and it is 32 -=> number of trees in X3, X4 are 32, 24 in any order.
So, number of trees in X2= 98-56-12=30
.’. Number of trees in Z1=69-30-28-8=3.
The final table will look like:

.’. Number of Mango trees=98.
Instructions
The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Question 7: Should a new person stand at intersection d, who among the six would she see?
a) W and X only
b) U and W only
c) U and Z only
d) V and X only
7) Answer (A)
Solution:
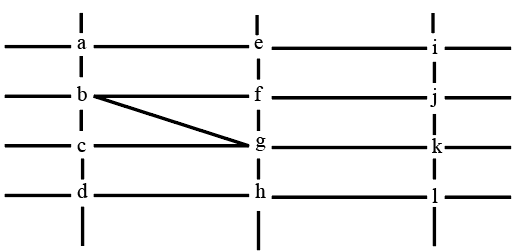
From 1, X, U, and Z are standing at the three corners of a triangle formed by three street segments.
From 2, X can see only U and Z.
From 4, U sees V standing in the next intersection behind Z. Also, no one among the six is standing at intersection d.
Only cases possible are:
1.
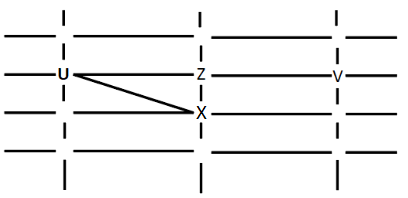
W cannot see V or Z. So W can only be at the intersection a. Since Y can see only U and W, Y can only be at c where X can see him. Hence this case is rejected.
2.
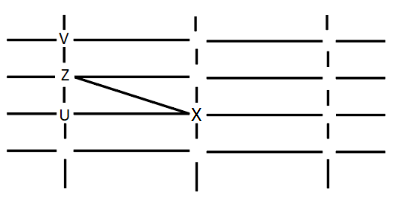
Y can only see U and W. Y cannot be placed anywhere. Hence this case is also rejected.
3.
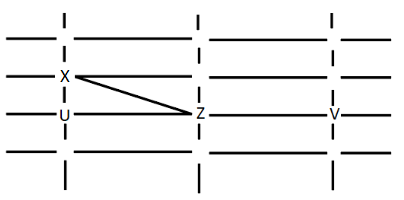
Y can only see U and W. Y cannot be placed anywhere. Hence this case is also rejected.
4.
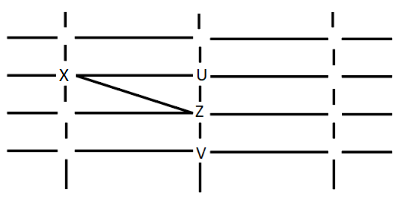
W cannot see V or Z. W can only be placed at i. Y can see only U and W. Y can only be placed at j or e, where he can see more people than U and W. Hence this case is also rejected.
5.
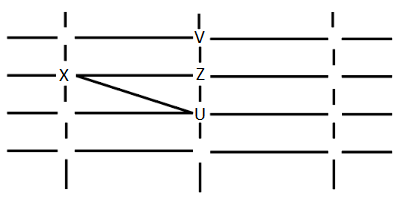
W cannot see V or Z. Y can only see U and W. Hence W and Y can only be placed as shown:
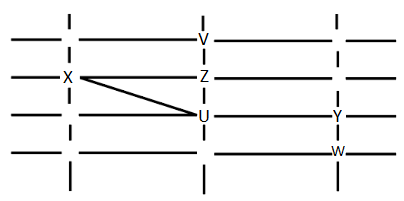
If a new person stands at d(left down corner), they can see W and X only. Hence A is the answer.
Question 8: What is the minimum number of street segments that X must cross to reach Y?
a) 1
b) 4
c) 2
d) 3
8) Answer (C)
Solution:

From 1, X, U, and Z are standing at the three corners of a triangle formed by three street segments.
From 2, X can see only U and Z.
From 4, U sees V standing in the next intersection behind Z. Also, no one among the six is standing at intersection d.
Only cases possible are:
1.

W cannot see V or Z. So W can only be at the intersection a. Since Y can see only U and W, Y can only be at c where X can see him. Hence this case is rejected.
2.

Y can only see U and W. Y cannot be placed anywhere. Hence this case is also rejected.
3.

Y can only see U and W. Y cannot be placed anywhere. Hence this case is also rejected.
4.

W cannot see V or Z. W can only be placed at i. Y can see only U and W. Y can only be placed at j or e, where he can see more people than U and W. Hence this case is also rejected.
5.

W cannot see V or Z. Y can only see U and W. Hence W and Y can only be placed as shown:

To reach Y, X has to go from b to g and g to k, i.e. 2 streets.
Question 9: Who can V see?
a) Z only
b) U, W and Z only
c) U and Z only
d) U only
9) Answer (C)
Solution:

From 1, X, U, and Z are standing at the three corners of a triangle formed by three street segments.
From 2, X can see only U and Z.
From 4, U sees V standing in the next intersection behind Z. Also, no one among the six is standing at intersection d.
Only cases possible are:
1.

W cannot see V or Z. So W can only be at the intersection a. Since Y can see only U and W, Y can only be at c where X can see him. Hence this case is rejected.
2.

Y can only see U and W. Y cannot be placed anywhere. Hence this case is also rejected.
3.

Y can only see U and W. Y cannot be placed anywhere. Hence this case is also rejected.
4.

W cannot see V or Z. W can only be placed at i. Y can see only U and W. Y can only be placed at j or e, where he can see more people than U and W. Hence this case is also rejected.
5.

W cannot see V or Z. Y can only see U and W. Hence W and Y can only be placed as shown:

V can see U and Z only. Hence C is the answer.
Question 10: Who is standing at intersection a?
a) W
b) Y
c) No one
d) V
10) Answer (C)
Solution:

From 1, X, U, and Z are standing at the three corners of a triangle formed by three street segments.
From 2, X can see only U and Z.
From 4, U sees V standing in the next intersection behind Z. Also, no one among the six is standing at intersection d.
Only cases possible are:
1.

W cannot see V or Z. So W can only be at the intersection a. Since Y can see only U and W, Y can only be at c where X can see him. Hence this case is rejected.
2.

Y can only see U and W. Y cannot be placed anywhere. Hence this case is also rejected.
3.

Y can only see U and W. Y cannot be placed anywhere. Hence this case is also rejected.
4.

W cannot see V or Z. W can only be placed at i. Y can see only U and W. Y can only be placed at j or e, where he can see more people than U and W. Hence this case is also rejected.
5.

W cannot see V or Z. Y can only see U and W. Hence W and Y can only be placed as shown:

No one is standing at the intersection A. Hence C is the answer.




![CAT Averages Questions PDF [Important Questions] CAT AVERAGES Questions PDF](https://cracku.in/blog/wp-content/uploads/2022/07/CAT-AVERAGES-Questions-PDF-218x150.png)
